LCL三相PWM整流器数学模型

基于LCL的三相电压型PWM整流器数学模型

LCL滤波器的三相PWM整流器结构如图所示
LCL 滤波的高频 PWM 整流器拓扑结构如图 2.6 所示。整流器侧是三个电阻为 R2 ，电感为 L 的电抗器，网侧是三个电阻为 R1，电感为 Lg 的电抗器，网侧电抗器和整流器侧电抗器之间是三个星型联结的电容器Cf 。电抗器 L 除滤波外，还具有升压及能量交换功能， Lg ，Cf 用于滤除高次谐波，满足电网对电流谐波的要求。

取单相 LCL 滤波的 PWM 整流器结构进行分析

式中：us ，uc ，ur ——电网电压、电容器电压、整流器侧控制电压
i1，ic ，i2——电网侧电流、电容器电流、整流器侧电流
由式（2-42），（2-43），（2-44）及前面开关函数的定义，可以推出 LCL 滤波的三相 PWM 整流器在三相电网电压对称情况下的开关数学模型

式中：udc ， RL ，C ——整流器直流侧电压、负载电阻及支撑电容
根据 KCL、KVL 得到三相静止 abc 坐标系下各相方程：

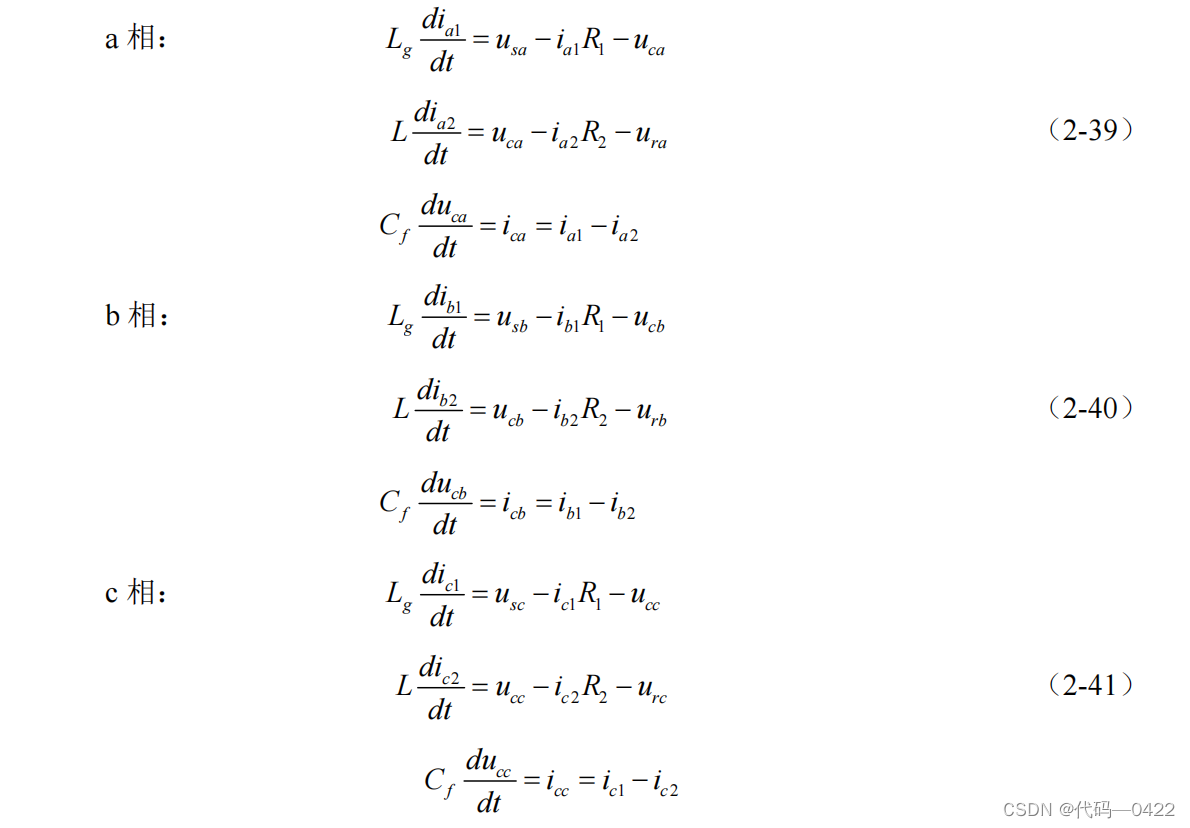
式中： sa sb sc uuu ， ， ——三相电网侧交流电压
uuu ca cb cc ， ， ——三相滤波电容上的电压
uuu ra rb rc ， ， ——整流器交流侧的三相电压
iii ， ， ——三相电网侧交流电流
222 abc iii ， ， ——整流器交流侧的三相电流


可以看出，三相 LCL 滤波器的状态空间方程为 9 阶的状态方程，对这样一个高
阶被控系统来说，如果不采用一定的方法进行降阶处理的话，则很难设计控制器。因此，对此状态方程进行abc →αβ 变换，按照式（2-25），（2-26）的转换矩阵，可得αβ
坐标系下的 LCL 滤波器状态空间方程为：

然后进行αβ → dq 根据式（2-29），（2-30）的变换矩阵，可得dq 坐标系下的 LCL
滤波器状态空间方程为：

式中：ωb ——三相电网电压的基波角频率
, sd sq u u ——三相电网电压矢量的 d，q 轴分量
, u u cd cq ——三相滤波电容电压矢量的 d，q 轴分量
, u u rd rq——整流器交流侧电压矢量的 d，q 轴分量
1 1 , i i d q——三相电网电流矢量的 d，q 轴分量
2 2 , i i d q ——整流器交流侧电流矢量的 d，q 轴分量
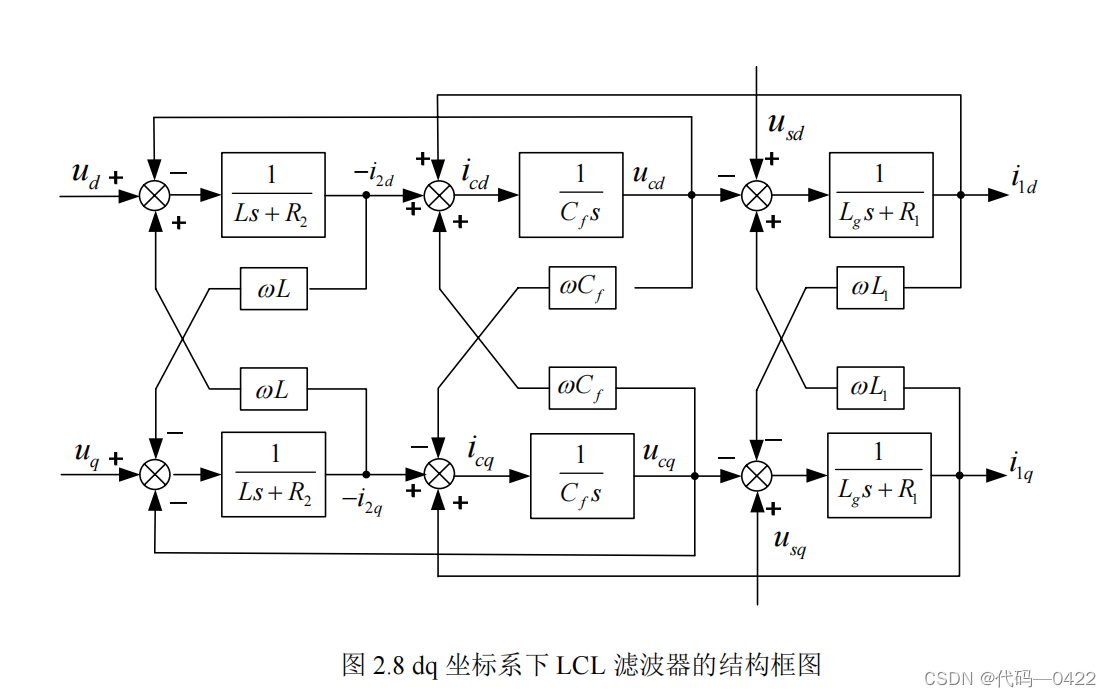
由式（2-44）可以得出图 2.8 所示的 LCL 滤波器的结构框图。控制的目的是给出
正确的控制矢量 r U& 使网侧电流与电压同相位。可以看出，基于 LCL 滤波器的 PWM
整流器是一个高阶、非线性、强耦合的多变量系统。