数字信号处理-08-FIR IP应用实例

FPGA and ICer

已于 2022-11-23 12:54:45 修改

阅读量1.5k

点赞数 4

分类专栏： # 数字信号处理FPGA实现文章标签： fpga开发 FIR滤波器数字信号处理

于 2022-08-10 22:30:35 首次发布

本文链接：https://blog.csdn.net/weixin_41445387/article/details/126275752

版权

数字信号处理FPGA实现专栏收录该内容

11 篇文章

订阅专栏

前言

本文根据FIR滤波器相关原理进行设计构建工程，利用前文的工程构建的混频功能的工程，将高频分量进行滤除，保留低频分量。

有限冲击响应滤波器概述

FIR滤波器广泛应用于数字信号处理中，主要功能就是将不感兴趣的信号滤除，留下有用信号。FIR滤波器是全零点结构，系统永远稳定；并且具有线性相位的特征，在有效频率范围内所有信号相位上不失真。相比IIR滤波器，FIR滤波器更容易用数字域进行实现。

在数字滤波的应用中，绝大部分接触的都是使用 FIR Filter，其相对于 IIR Filter 要简单的多。FIR Filter 的核心思想就是卷积运算，然后了解一下卷积的时域卷积定理，就可以想象出 FIR 滤波器的原理。

FIR滤波器的设计方法

FIR滤波器要在FPGA或其他硬件平台上按所需结构实现满足要求的FIR滤波器，关键问题就在于设计出滤波器的单位脉冲响应，或者说是FIR滤波器各级延时单元的加权系数。

因为各种实现结构均是基于滤波器的单位脉冲响应进行设计的。对于一个线性时不变系统，系统的单位脉冲响应也完全可以表示系统各项特征。

FIR滤波器的设计方法有窗函数法、频率取样法及等波纹优化设计方法等，下面分别进行介绍。

窗函数法

窗函数法是一种在时域设计FIR数字滤波器的方法，是设计FIR数字滤波器最简单，也是使用最普遍的方法。窗函数法的基本思路是先给出要求的理想滤波器频率响应Hd(e^{jw)，然后设计一个FIR滤波器频率响应H(e}jw)去逼近Hd(e^jw)。

由于窗函数法是在时域进行的，因此首先需要由理想频率响应推导出对应的单位取样响应h(n)，再设计一个FIR数字滤波器的单位取样响应h(n)去逼近hd(n)。

加窗后对理想滤波器的特性主要有以下几点影响。

Hd(w)在截止频率处的间断点变成了连续曲线，使实际滤波器的幅频特性出现了一个过渡带。
由于窗函数旁瓣的作用，使幅频特性出现波动，波动幅度取决于旁瓣的相对幅度，旁瓣范围的面积越大，通带波动和阻带波动越大。
增加窗函数的长度，只能减少主瓣宽度，而不能改变旁瓣与主瓣的相对值，该值取决于窗函数的形状。

因此，为了满足工程上的要求，只能以改变窗函数的形状来改善滤波器的幅频特性。窗函数的选择原则是:

具有较低的旁瓣幅度，尤其是第一旁瓣幅度。
旁瓣幅度下降速率要大，以利于增加阻带衰减。
主瓣的宽度要窄，以获得较陡的过渡带。

频率取样法

窗函数法是从时域出发设计滤波器。一个有限长序列，在满足频率采样定理的条件下，可以通过对频谱的有限个采样值准确地恢复原序列频率取样法设计FIR滤波器就是从频域出发，根据频域采样定理，对给定的理想频率响应Hd(e^jw)进行等间隔采样。

最优设计方法

前面讲述了两种FIR滤波器设计方法。窗函数法不容易设计预先给定截止频率的滤波器，也未能解决在给定阶数N值时，怎样设计一个最佳FIR滤波器的问题。频率取样法是一种优化设计，但因赖以进行优化设计的变量只限于过渡带上几个采样值，故不是最优化的设计。从FIR滤波器的系统函数可以看出，极点都在Z平面的原点，不同的零点分布对应不同的频率响应。最优设计实际上就是调节这些零点分布位置，使实际频率响应H(e)与理想频率响应H(e)间的绝对偏差最小。接下来将讨论的最优设计方法——等波纹切比雪夫逼近法，采用“最大误差最小”准则得到最佳滤波器，且最佳解唯一。

在实际设计中，通常要求线性相位滤波器在不同的频带内逼近的误差不同。如通带内最大允许误差不超过一个范围，阻带内最大允许误差不超过一个范围。切比雪夫等波纹逼近是采用加权逼近误差Hd(e^jw)最小为出发点设计滤波器的方法。

卷积类比FIR卷积

在离散数字信号领域，卷积的定义如下
$\sum_{i=-\infty}^\infty 𝑥(𝑖)ℎ(𝑛 - 𝑖) = 𝑥(𝑛) ∗ ℎ(𝑛)\\$
而 FIR Filter 中的卷积是有限长序列的卷积，定义为
$\sum_{k=0}^{M-1} 𝑥(k)ℎ(𝑛 - k) = 𝑥(𝑛) ∗ ℎ(𝑛)$
其中ℎ(𝑘)是滤波器序列， M 是滤波器系数的长度， k 的取值为 0~M-1。在实际的应用中，一般都会认为𝑥(𝑛)的也是从零开始。下面举一个例子，设置一个序列和一个滤波器系数，然后观察卷积效果。

xn=[5,11,15,234,34,67,88,46,66,12];%定义x(n)序列
m=size(xn,2);
t1=0:m-1;%定义时间
hn=[0.2,0.2,0.2,0.2,0.2];%定义h（n）序列
n=size(hn,2);
t2=0:n-1;
yn=conv(xn,hn);
t3=0:(n+m-1)-1;%卷积计算后序列的长度定义为n+m-1
figure;
subplot(3,1,1);stem(t1,xn,'r','filled');title('x(n)序列');%画x(n)序列
subplot(3,1,2);stem(t2,hn,'g','filled');title('h(n)序列');%画h(n)序列
subplot(3,1,3);stem(t3,yn,'b','filled');title('y(n)序列');%画y(n)序列

经过卷积运算后的信号序列更加平滑，观察hn序列中的系数均为0.2，该设计类似一个平滑滤波器的功能，相当于做了平均滤波。

利用MATLAB或filter_solution设计滤波器

DDS的混频工程，混频之后的信号是 1Mhz 和 7Mhz，保留低频分量的话就要滤除 7Mhz 保留 1Mhz。因为IP中设置的信号动态范围是 45dB，那么1Mhz 和 7Mhz 的动态范围各自是22.5dB，要想把7Mhz 抑制掉，需要至少滤波器要抑制信号 22.5dB。所以设计的滤波器，在 9Mhz位置需要是有至少-22.5dB 的衰减，且在1Mhz 位置通带尽量平滑，并接近于 0dB，也就是没有增益没有衰减。

在这里可以利用MATLAB的滤波器设计工具或者Filter_solution进行构建。

MATLAB的FDA设计

下图为滤波器设计的界面，通过界面可以设计所需要的滤波器，为了滤除设计中的高频分量，这里使用了低通滤波，并根据实际的应用需求将参数进行设置。

滤波类型（Filter Type）= Lowpass
采样率（Fs） = 50MHZ
滤波阶数（order） = 63（阶数越大，滤波品质越好，但相对滞后越大）
密度因子（ Density Factor）= 20
Fpass（通频带）= 2MHZ
Fstop（截止带）= 4MHZ
Apass（通频带宽增益期望）= 1dB
Astop（截止带宽增益期望）= -80dB

完成滤波器的参数配置后，进行生成滤波器的系数，点击下图指示可生成coe文件或者c的头文件，可根据具体需要进行输出设置。

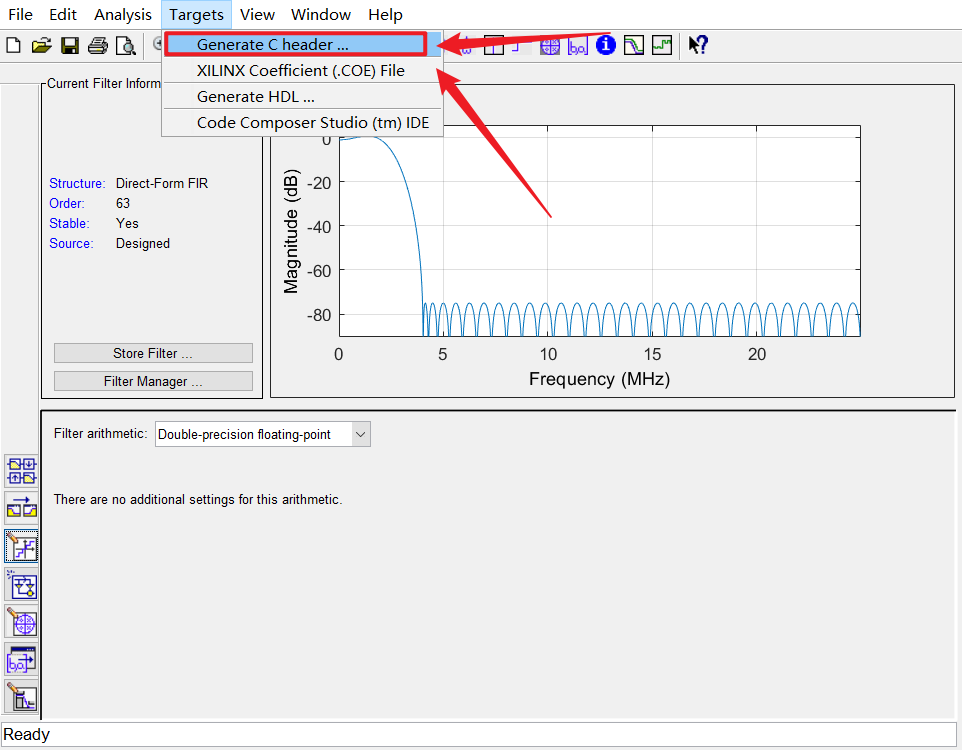
filter_solution设计滤波器

该软件效果和MATLAB的滤波器的效果相当，都是根据需求调整相应的滤波器参数，然后进行生成相关的滤波器系数。

点击频率响应可观察到该滤波器的频率响应图。

如下图所示：

点击分析滤波器可获得相关滤波器的权值。可根据具体需求选择输出向量模式或者生成相关测试C代码。

使用FIR IP进行工程设计

将DDS应用实例的工程进行复制备份，然后添加FIR IP。打开设置相关参数。

FIR滤波器IP设置

可先在第一个界面配置滤波器的基本参数，如果滤波器系数选择向量格式，可将刚刚在滤波器设计软件中的系数进行复制，并粘贴到vector的输入框中。这里将之前生成的系数进行复制。

8.05e-04, 8.416e-04, 8.681e-04, 8.624e-04, 7.882e-04, 6.001e-04, 2.496e-04, -3.048e-04, -1.089e-03, -2.101e-03, -3.306e-03, -4.628e-03, -5.95e-03, -7.117e-03, -7.941e-03, -8.217e-03, -7.735e-03, -6.301e-03, -3.758e-03, 0, 5.008e-03, 1.122e-02, 1.85e-02, 2.664e-02, 3.533e-02, 4.421e-02, 5.289e-02, 6.095e-02, 6.798e-02, 7.361e-02, 7.754e-02, 7.956e-02, 7.956e-02, 7.754e-02, 7.361e-02, 6.798e-02, 6.095e-02, 5.289e-02, 4.421e-02, 3.533e-02, 2.664e-02, 1.85e-02, 1.122e-02, 5.008e-03, 0, -3.758e-03, -6.301e-03, -7.735e-03, -8.217e-03, -7.941e-03, -7.117e-03, -5.95e-03, -4.628e-03, -3.306e-03, -2.101e-03, -1.089e-03, -3.048e-04, 2.496e-04, 6.001e-04, 7.882e-04, 8.624e-04, 8.681e-04, 8.416e-04, 8.05e-04

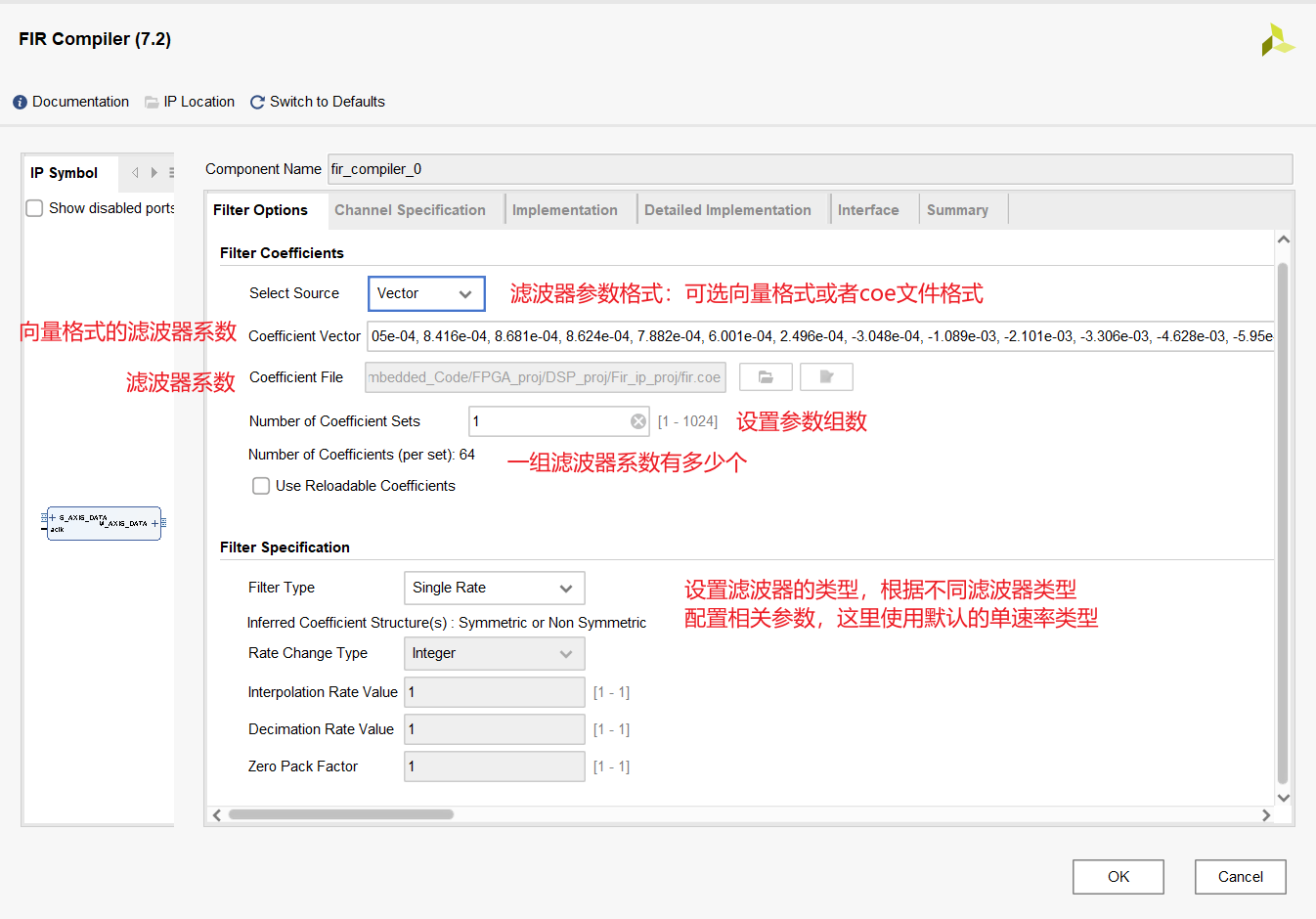
然后可以对通道相关参数进行设置。

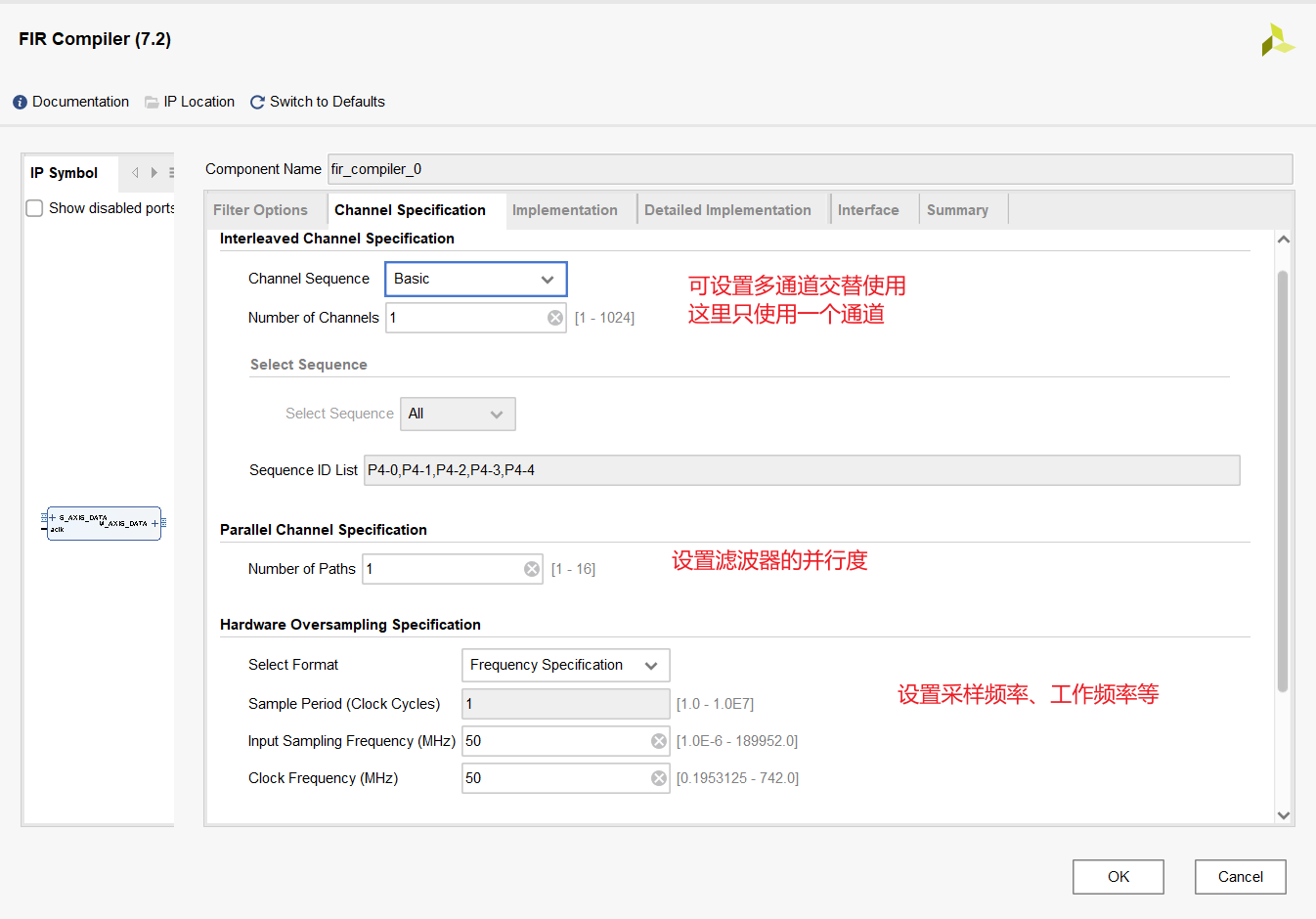
在第三个界面中可设置滤波器系数的相关数据格式，以及输入输出的数据格式。需要注意的是，这里输入的信号是DDS产生的数据，这个数据仅有整数部分，所以要调整输入数据的小数位为0。

详细实现界面主要对滤波器的硬件实现的架构进行选择，包括对架构的优化方式，存储以及DSP资源的使用设置。

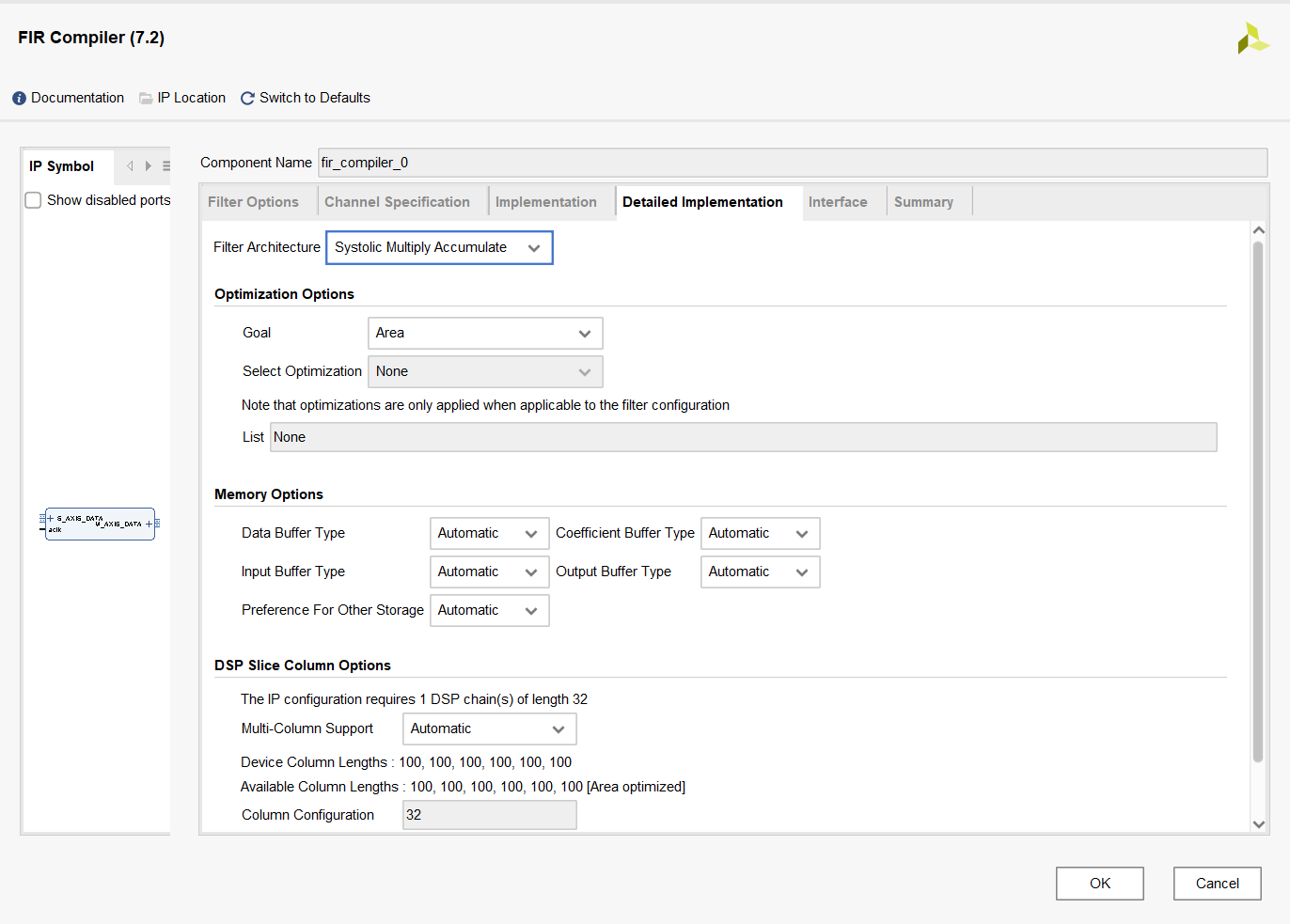
接口界面主要对相关的指示信号进行设置，这里可暂时保持默认，实际应用时可根据需要进行使能相关信号。

总结界面对前面的相关设置进行了小结展示，方便用户进行检查核对并修改错误设置的参数。

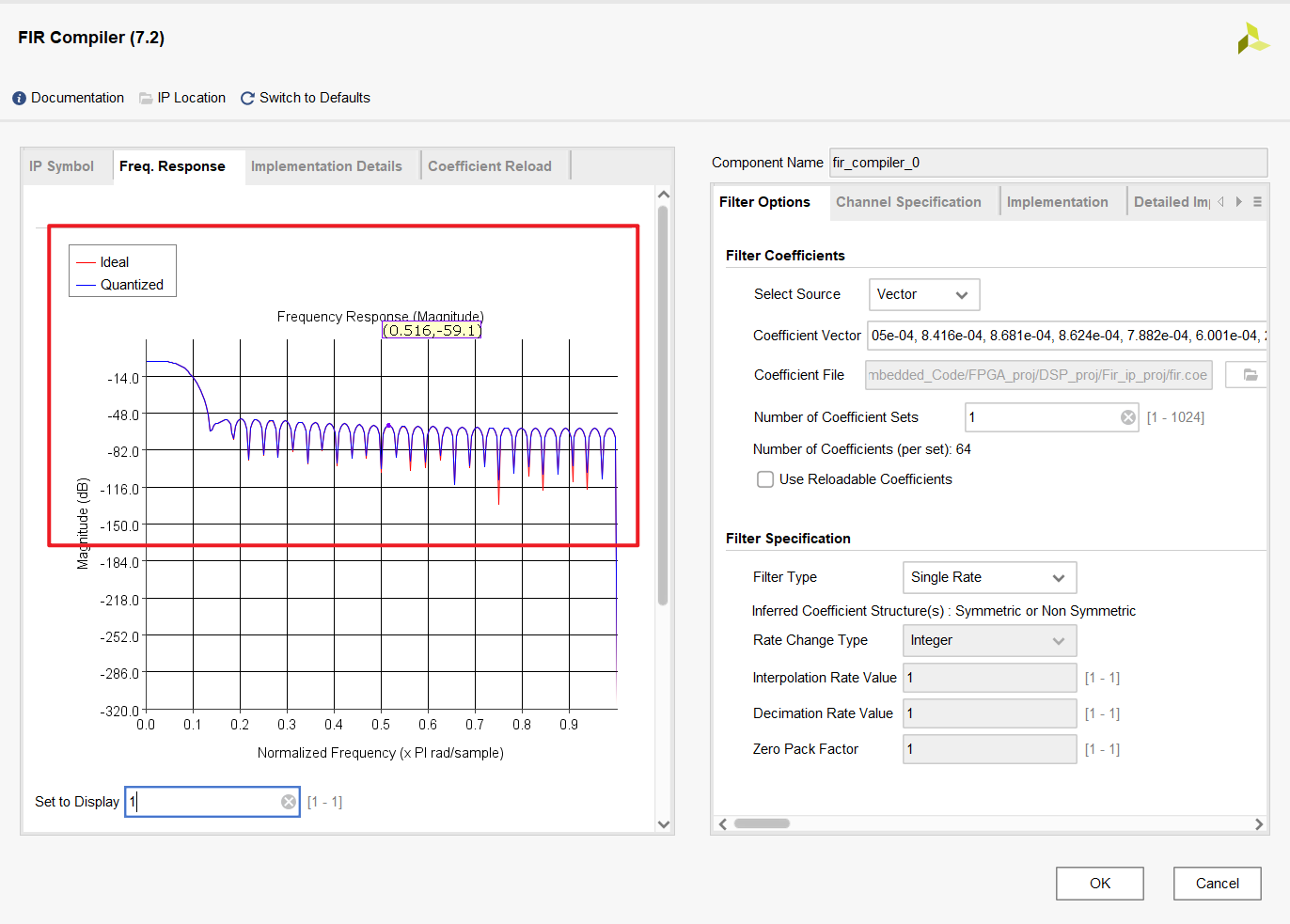
同时在左侧栏中可以看到滤波器的频率响应，以及该IP设置的相关资源使用情况，以便于在实际工程应用中对数据链路的信号进行操作处理，以及对资源的合理分配。

修改DDS IP

之前进行混频设计时，使用了DDS的IP输出三路信号分别为10MHz，3MHz和4MHz。这里为了减少一路输出，设置两路的信号输出，匹配FIR的ip采样频率的50MHz。或者这里采用频率直接修改为33.33MHz也可以。

修改顶层文件

修改了DDS ip后，要对逻辑进行调整使得可根据m_axis_data_tuser信号输出3M和4M的信号。并在顶层模块中调用例化FIR的IP，将混频后的数据接入到FIR的输入数据端，将DDS的data_tvalid接到FIR ip的tvalid端口，tready可悬空。因为仿真设计的是100MHz时钟，而FIR ip需要的是50MHz所以用寄存器生成一个二分频时钟接入到FIR ip的时钟端口。

module top(
    input clk
    );

    // wire m_axis_data_tvalid_ch1;
    // wire [7:0] m_axis_data_tdata_ch1;
    // //单通道测试
    // dds_compiler_0 ch1_dds(
    // .aclk(clk),                              // input wire aclk
    // .m_axis_data_tvalid(m_axis_data_tvalid_ch1),  // output wire m_axis_data_tvalid
    // .m_axis_data_tdata(m_axis_data_tdata_ch1)    // output wire [7 : 0] m_axis_data_tdata
    // );
    wire          m_axis_data_tvalid_ch3;
    wire [7 : 0]  m_axis_data_tdata_ch3;
    wire [0 : 0]  m_axis_data_tuser_ch3;
    // wire          m_axis_phase_tvalid_ch3;
    // wire [31 : 0] m_axis_phase_tdata_ch3;
    // wire [1 : 0]  m_axis_phase_tuser_ch3;

    //多通道测试
    dds_compiler_1 multi_ch_dds(
    .aclk(clk),                                // input wire aclk
    .m_axis_data_tvalid (m_axis_data_tvalid_ch3),    // output wire m_axis_data_tvalid
    .m_axis_data_tdata  (m_axis_data_tdata_ch3),      // output wire [7 : 0] m_axis_data_tdata
    .m_axis_data_tuser  (m_axis_data_tuser_ch3),      // output wire [1 : 0] m_axis_data_tuser
    .m_axis_phase_tvalid(),  // output wire m_axis_phase_tvalid
    .m_axis_phase_tdata (),    // output wire [31 : 0] m_axis_phase_tdata
    .m_axis_phase_tuser ()    // output wire [1 : 0] m_axis_phase_tuser
    );
    reg [7 : 0] data10MHz;
    reg [7 : 0] data3MHz;
    reg [7 : 0] data4MHz;
    always @(posedge clk) begin
        case(m_axis_data_tuser_ch3)
            0:data3MHz<=m_axis_data_tdata_ch3;
            1:data4MHz<=m_axis_data_tdata_ch3;
        endcase
     end
    //混频测试
    wire [15 : 0]  mixer_singal;
    mult_gen_0 mult_mixer (
        .CLK(clk),  // input wire CLK
        .A(data3MHz),      // input wire [7 : 0] A
        .B(data4MHz),      // input wire [7 : 0] B
        .P(mixer_singal)      // output wire [15 : 0] P
    );
    wire [39:0] after_fir_singal;
    reg div_clk=0;
    always @(posedge clk ) begin
        div_clk<=!div_clk;
    end
    fir_compiler_0 uut_fir(
    .aclk(div_clk),                              // input wire aclk
    .s_axis_data_tvalid(m_axis_data_tvalid_ch3),  // input wire s_axis_data_tvalid
    .s_axis_data_tready(s_axis_data_tready),  // output wire s_axis_data_tready
    .s_axis_data_tdata(mixer_singal),    // input wire [15 : 0] s_axis_data_tdata
    .m_axis_data_tvalid(m_axis_data_tvalid),  // output wire m_axis_data_tvalid
    .m_axis_data_tdata(after_fir_singal)    // output wire [39 : 0] m_axis_data_tdata
    );
endmodule

运行仿真测试

点击运行行为级仿真，添加信号波形，并修改信号的进制（进制可选择有符号十进制）和类型（选择模拟类型），可观察到下面的情况。

从截图中可看出，混频后的信号经过了滤波处理消除了高频分量，添加游标可观察滤波后的信号的频率。添加游标后观察发现滤波后的信号为混频信号的1Mhz的信号。因此，工程设计中的低通滤波很好地滤除掉了7MHz的高频分量。

小结思考

在使用FIR滤波器中的实际设计的数字滤波器效果可能会因设置的不同而效果不同。因此，在实际使用时要关注一下方面确保滤波器的效果能达到预期。

在滤波器工具使用时应考虑不同类型的滤波器的实际效果，可经过对比选择性能较优异，阶数少，且滤波效果能达到使用预期的类型，例如在使用FIR滤波器时，同样阶数的不同类型窗的滤波效果可能对特定信号的滤波效果不同。
该工程仅仅验证了FIR滤波器的基本功能，在实际使用时特别是遇到实时处理的情况需谨慎考虑滤波器的并行度，确保在规定的处理时间内能完成相关信号处理操作，且要关注数据链路的数据位宽，确保在实际应用做切片处理时不会损失精度，或造成数据溢出。