【数据分析】03- 拒绝拍脑袋！用相关分析洞悉变量秘密，一文搞定数据探索：从“皮尔逊相关系数”到“肯德尔相关系数”

下面这篇文章将以循序渐进的方式，深入解析「相关分析（Correlation Analysis）」的来龙去脉，从历史发展到实际应用，再到不同相关系数的适用场景。希望能帮助你在项目实践中灵活运用相关分析。如果觉得不错，别忘了 点赞、收藏、评论、转发 给更多小伙伴哦！

深度解读相关分析与相关系数

---

一、背景与发展

在大数据浪潮下，相关分析（Correlation Analysis）已成为我们探秘万物规律的重要“放大镜”，它主要研究两个或多个变量之间是否存在某种线性关联以及关联强度的大小。可以想象，如果我们想知道“咖啡销量”和“深夜加班人数”之间是否同涨同跌，那么相关分析便能满足我们的好奇心。

从最早的皮尔逊相关系数（Pearson Correlation）到如今多样的非参数检验方法（如斯皮尔曼等级相关（Spearman's Rank Correlation）和肯德尔相关（Kendall's Tau）），相关分析已经形成了一套相对成熟的数学统计体系。随着数据科学与机器学习的迅猛发展，相关分析不仅在学术研究中广受青睐，也成为各行业数据分析过程中的“常规操作”，例如市场营销中的用户画像、经济学中的消费与收入分析、医疗健康中的药物剂量与疗效研究等，都离不开它的助力。

---

1.1 早期萌芽：好奇“花色”和“蜜蜂到访”究竟有无关系？

想象一下，若在郁郁葱葱的英伦花园里，有人注意到“某些特别鲜艳的花，好像吸引更多蜜蜂”。他可能想问：“花色程度跟蜜蜂到访数量之间，是不是有某种线性规律？” 这就初步触发了相关分析的概念。

---

其实在 19 世纪下半叶，生物学家和统计学家开始察觉，很多生物和社会现象都呈现“齐涨共跌或一升一降”的规律。例如：

• 身高与体重；

• 父母身高与孩子身高；

• 经济指标与股市波动等。

---

1.2 卡尔·皮尔森（Karl Pearson）与弗朗西斯·高尔顿（Francis Galton）

• 弗朗西斯·高尔顿提出了早期的回归与相关思想；

• 卡尔·皮尔森则在此基础上给出了一套更系统的公式化方法，“皮尔森相关系数”应运而生。

• 随后，统计学家又扩展出非线性和秩次（排序）相关系数，满足了更多数据形态的需求。今天的相关分析已经成为数据科学与大数据分析中的常见基础工具。

---

二、相关分析的核心概念：它是啥？有什么用？

2.1 相关分析定义：

相关分析（Correlation Analysis）主要用于衡量两个或多个变量之间的“线性关系”强度和方向。例如：如果你想知道“复习时间”与“考试成绩”之间是正相关（时间越长成绩越好）还是负相关（时间越长成绩反而下降……这就很怪）或是完全没关系，就可以用相关分析做定量评估。

---

2.2 相关分析用途：

1. 探索性数据分析（EDA）：快速找出数据集中哪些变量之间强相关或弱相关，为后续建模、特征工程提供线索。

2. 特征选择：在机器学习中，如果两个特征强相关，可能存在多重共线性；适度去除冗余特征可简化模型。

3. 学术研究：社会科学、心理学或医学研究中，也常用相关分析来验证自变量与因变量是否存在一定线性关系。

注意：相关不代表因果！相关分析只能告诉你两个变量“齐涨共跌”或“反向变动”，但无法保证“谁导致了谁”。

三、几种常见的相关系数：皮尔逊、斯皮尔曼、肯德尔相关系数

3.1 皮尔逊相关系数（Pearson Correlation）

1. 原理：

2. 适用场景：

• 数据为连续且近似正态分布；

• 或者至少具有线性特征。

• 最常见，如身高 vs. 体重、复习时长 vs. 分数等。

3. 优点和局限：

• 优点：计算简单，解释直观；

• 局限：对“异常值”或“非线性关系”非常敏感，如果数据呈曲线或有一些极端值，皮尔逊相关系数容易失真。

---

3.2 斯皮尔曼等级相关系数（Spearman’s Rank Correlation）

1. 原理：

• 把数据转化为各自的秩（排名），然后计算皮尔逊相关系数。

• 公式可写为：

2. 适用场景：

• 数据非正态或非线性，但仍有单调关系（随 x 递增，y 也递增或递减）；

• 数据有明显的异常值，用秩次取代原值能降低异常值影响。

3. 优点：

• 对非线性但“单调”关系也能捕捉；

• 不要求数据服从正态；

• 异常值影响相对更小。

---

3.3 肯德尔相关系数（Kendall’s Tau）

1. 原理：

• 主要基于对排序对偶的一致性来量化相关，判断“两个序列中有多少对数据的排序是一致或不一致”。

2. 适用场景：

• 跟 Spearman斯皮尔曼等级 类似，都用于秩次数据；

• 在某些只关心“排名次序”的场合更适用。

3. 常用情形：

• 社会科学研究时，对调研问卷的 ordinal 数据做分析；

• 对“比较偏离高斯分布”的数据，考量秩次关系更稳健。

---

四、应用场景选择合适的相关系数

4.1 相关分析的意义与应用场景

• 数据清洗与特征选择
  在机器学习的特征工程阶段，若发现两个特征强相关，通常会只保留一个，以免后续模型训练时出现多重共线性问题。

• 假设检验与研究发现
  社会学或心理学研究常常通过收集问卷数据，先利用相关分析初步发现潜在关系，再进行更深入的因果推断或回归分析。

• 可视化与数据探查
  在初步的探索性数据分析（EDA）中，相关系数和配套的相关热力图是“排雷”法宝，能快速帮我们瞄准变量之间显著的联系。

4.2 如何选择合适的相关系数？

1. 数据分布：若是连续、线性、无异常点，可选皮尔逊；如果非线性或有异常点，考虑 Spearman 或 Kendall。

2. 度量水平：若数据只是名义或顺序（如名次、等级）属性，则 Spearman、Kendall 更合适。

3. 对异常值敏感度：若异常值较多且你不想被它们左右结果，Spearman / Kendall 通常更安全。

---

五、案例：小例子让你学会相关分析：Python 实战

---

5.1 简单的案例demo

• 我们收集了 10 个大学生的“每日学习时长（小时）”和“考试分数”，想看看它们的关系如何。

• 又假设我们在另一个调查中，记录了“吃辣程度排名”与“耐热程度排名”，看看二者是否保持单调关系。

---

5.1.1 简易代码示例（Python）

import numpy as np
import pandas as pd
from scipy.stats import pearsonr, spearmanr, kendalltau

# 假设: 学习时长(hour) & 考试分数
study_time = np.array([2, 3, 5, 1, 4, 4.5, 6, 2.5, 3.5, 4])
exam_score = np.array([65, 70, 85, 60, 76, 78, 92, 68, 73, 80])

# 1. Pearson
pearson_corr, p_val_pearson = pearsonr(study_time, exam_score)

# 2. Spearman
spearman_corr, p_val_spearman = spearmanr(study_time, exam_score)

# 3. Kendall
kendall_corr, p_val_kendall = kendalltau(study_time, exam_score)

print(f"Pearson相关系数: {pearson_corr:.2f} (p={p_val_pearson:.4f})")
print(f"Spearman相关系数: {spearman_corr:.2f} (p={p_val_spearman:.4f})")
print(f"Kendall相关系数: {kendall_corr:.2f} (p={p_val_kendall:.4f})")

输出：

• 若 Pearson 相关系数约 0.8 且 p 值很小，就意味着“学习时长和考试分数高度正相关”——再结合逻辑推断，你或许会说“多复习真的有帮助”。

• 对于“吃辣排名 vs. 耐热排名”，因为它本质更偏秩序类型，可以用 spearmanr 或 kendalltau 分析。

---

5.2 一步步学会相关分析：Python 实战

接下来，咱们从零开始，用一个公开的示例数据集来演示如何进行相关分析。为了方便，我们使用 Python 中非常常见的 seaborn 自带的示例数据集 “tips”（小费数据）。该数据集包含了服务员小费的相关信息，如消费总金额、用餐时间、用餐人数、性别等。

环境准备：

• Python 3.x
• 相关库：pandas, numpy, matplotlib, seaborn

1. 数据获取与初步了解

# 导入必要的库
import seaborn as sns  # Seaborn 是一个基于 Matplotlib 的数据可视化库，提供高水平的图形接口。
import pandas as pd  # Pandas 是一个数据分析库，用于处理和分析表格型数据。
import matplotlib.pyplot as plt  # Matplotlib 是一个底层绘图库，用于创建各种可视化图表。

# 使用 Seaborn 加载内置的示例数据集 'tips'
tips = sns.load_dataset('tips')  
# 'tips' 数据集是 Seaborn 提供的一个示例数据集，包含顾客在餐厅消费的小费数据，以下是数据的字段：
# - `total_bill`：总消费金额（浮点型）
# - `tip`：小费金额（浮点型）
# - `sex`：服务员性别（分类变量：'Male' 或 'Female'）
# - `smoker`：顾客是否吸烟（分类变量：'Yes' 或 'No'）
# - `day`：星期几（分类变量，如 'Sun', 'Sat' 等）
# - `time`：用餐时间（分类变量：'Lunch' 或 'Dinner'）
# - `size`：用餐人数（整数型）

# 打印数据集的前 5 行，便于查看其结构和内容
print(tips.head())
# `head()` 方法显示数据框的前 5 行，默认为 5 行。如果需要查看更多行，可以传递参数，例如 `tips.head(10)`。

输出： 

---

2. 绘制散点图初探

我们先用散点图直观感受一下 total_bill（总消费）和 tip（小费）这两个变量的关系。

# 设置绘图的画布大小
plt.figure(figsize=(6, 4))
# `plt.figure()` 用于创建一个新的绘图窗口。
# `figsize=(6, 4)` 设置画布大小，宽度为 6 英寸，高度为 4 英寸。

# 使用 Seaborn 绘制散点图
sns.scatterplot(x='total_bill', y='tip', data=tips)
# `sns.scatterplot()` 用于绘制散点图。
# 参数说明：
# - `x='total_bill'`：设置 x 轴为 `total_bill`（总消费金额）。
# - `y='tip'`：设置 y 轴为 `tip`（小费金额）。
# - `data=tips`：指定数据来源为 `tips` 数据集。
# 该散点图展示了总消费金额与小费金额的关系。

# 设置图表标题
plt.title('总消费 vs 小费')
# `plt.title()` 用于设置图表的标题，标题为“总消费 vs 小费”。

# 显示绘图
plt.show()
# `plt.show()` 用于显示绘制的图表。

输出：

从散点分布可以大致看出，小费与总消费似乎呈现某种程度上的正向关系——消费越高，小费也倾向于更高。但这只是视觉上的感受，接下来就要用定量的方法：相关分析。

---

3. 皮尔逊相关系数计算

import numpy as np  # 导入 NumPy 库（在此代码中未直接使用，但可能为后续扩展准备）。

# 计算皮尔逊相关系数
pearson_corr = tips['total_bill'].corr(tips['tip'], method='pearson')
# 使用 Pandas 的 `corr()` 方法计算 `total_bill` 和 `tip` 两列之间的皮尔逊相关系数。
# 参数说明：
# - `tips['total_bill']`：数据集中的 `total_bill` 列（总消费金额）。
# - `tips['tip']`：数据集中的 `tip` 列（小费金额）。
# - `method='pearson'`：指定使用皮尔逊相关系数方法。
# 皮尔逊相关系数用于衡量两个变量之间的线性相关性，其值范围为 -1 到 1

print("皮尔逊相关系数（total_bill vs tip）:", pearson_corr)
# 打印皮尔逊相关系数结果。
# 输出结果将显示 `total_bill` 和 `tip` 两列数据之间的相关性大小和方向。

输出：

• 如果结果接近 1，说明两者强正相关；
• 如果结果接近 -1，说明两者强负相关；
• 如果结果接近 0，说明两者线性相关程度不高。

在这个例子中，小费与消费金额通常会得到一个大约在 0.67左右的相关系数（可能会因数据源更新略有波动），呈正相关，这也符合日常经验：谁会在只花了5块钱的情况下还潇洒地给10块钱小费呢？

---

4. 斯皮尔曼相关系数与肯德尔相关系数

如果我们要查看排序层面的关系，可以试试斯皮尔曼和肯德尔。

spearman_corr = tips['total_bill'].corr(tips['tip'], method='spearman')
kendall_corr = tips['total_bill'].corr(tips['tip'], method='kendall')
print("斯皮尔曼相关系数:", spearman_corr)
print("肯德尔相关系数:", kendall_corr)

输出： 

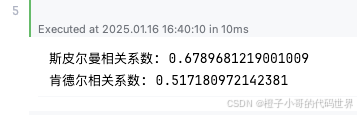
通常情况下，这两个值也都会落在 0~1 的正相关范围内，但数值往往会比皮尔逊系数略小一些。这是由于它们侧重排名的相似度，对数值规模的大小敏感度较低，但足以说明两者之间存在正向的单调关系。

---

5. 一次性查看所有数值型变量之间的相关性

在真实场景中，数据集往往有许多特征，我们可以来一把“大扫除”，直接查看所有数值变量之间的相关系数矩阵，并用热力图可视化。

numeric_tips = tips.select_dtypes(include=['number'])
corr_matrix = numeric_tips.corr() # 默认皮尔逊相关系数 method='pearson'
print(corr_matrix)
plt.figure(figsize=(6, 4))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', fmt='.2f')
plt.title('Tips 数据集相关系数热力图 (Pearson)')
plt.show()

输出：

通过这张热力图，我们不仅能观察到 total_bill 与 tip 的正相关关系，还能发现其他的一些潜在关联。例如 size（用餐人数）与 total_bill 之间是否明显正相关、和 tip 之间的关系又如何等等。我们就可以针对显著相关或不相关的变量进一步“抠细节”。

5.3 案例：特征选择中的相关分析

问题描述： 在房价预测模型中，有多种特征，如面积、房间数量、楼层等。如何选择与房价相关性高的特征，提升模型性能？

解决方案： 计算各特征与房价的皮尔逊相关系数，选择相关性高的特征进行建模。

问题描述： 在构建多变量回归模型时，发现部分特征之间存在高度相关性，如何检测和处理多重共线性问题？

解决方案： 通过计算自变量之间的相关系数矩阵，识别高度相关的特征，并采取措施如删除或合并相关特征。

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split

# Step 1: 生成模拟数据
np.random.seed(0)  # 设置随机种子，确保结果可复现
area = 2.5 * np.random.randn(100) + 25  # 房屋面积（平方米），服从正态分布，均值为 25，标准差为 2.5
rooms = np.random.randint(1, 5, 100)  # 房间数量，随机生成 1 到 4 的整数
floors = rooms  # 假设楼层数量与房间数量完全相关（这会导致共线性问题）
price = (50 + 20 * area + 30 * rooms + 
         np.random.randn(100) * 10)  # 房价（万元），基于面积、房间数，添加随机噪声

# Step 2: 构建数据表
data = pd.DataFrame({
    'Area': area,   # 房屋面积
    'Rooms': rooms, # 房间数量
    'Floors': floors, # 楼层数量
    'Price': price   # 房价
})

# Step 3: 计算相关系数矩阵
correlation_matrix = data.corr()  # 计算变量之间的相关系数矩阵
print(correlation_matrix)  # 打印相关系数矩阵

# Step 4: 可视化相关系数矩阵
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm')  
# 使用 Seaborn 绘制热图，annot=True 表示在热图上显示具体数值，cmap='coolwarm' 表示颜色映射
plt.title('相关系数矩阵')  # 设置热图标题
plt.show()  # 显示热图

# Step 5: 发现共线性问题并处理
# 从相关系数矩阵中可见，Rooms 和 Floors 完全相关（相关系数为 1.0）
# 为避免共线性对模型产生影响，删除 Floors 特征
X = data[['Area', 'Rooms']]  # 选择房屋面积和房间数量作为模型的输入特征
y = data['Price']  # 将房价作为目标变量

# Step 6: 训练线性回归模型
model = LinearRegression()  # 创建线性回归模型实例

# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 训练模型
model.fit(X_train, y_train)

# 使用测试集进行预测
y_pred = model.predict(X_test)

# 评估模型在测试集上的表现
mse = mean_squared_error(y_test, y_pred) # 计算均方误差
r2 = r2_score(y_test, y_pred)  # 计算决定系数（R²）
print(f'测试集均方误差: {mse:.2f}') # 打印均方误差，数值越小越好
print(f'测试集决定系数: {r2:.2f}')  # 打印决定系数，接近 1 表明拟合效果好


plt.scatter(y_test, y_pred, color= 'purple')   # 绘制散点图，x 为真实房价，y 为预测房价
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--', lw=2)
# 绘制一条黑色虚线，表示理想预测值与真实值相等的情况
# 'k--'：k 表示黑色，-- 表示虚线；lw=2 表示线宽为 2
plt.xlabel('真实价格')  # 设置 x 轴标签
plt.ylabel('预测价格')  # 设置 y 轴标签
plt.title('真实值 vs 预测值')  # 设置图标题
plt.show()  # 显示图像

输出： 

---

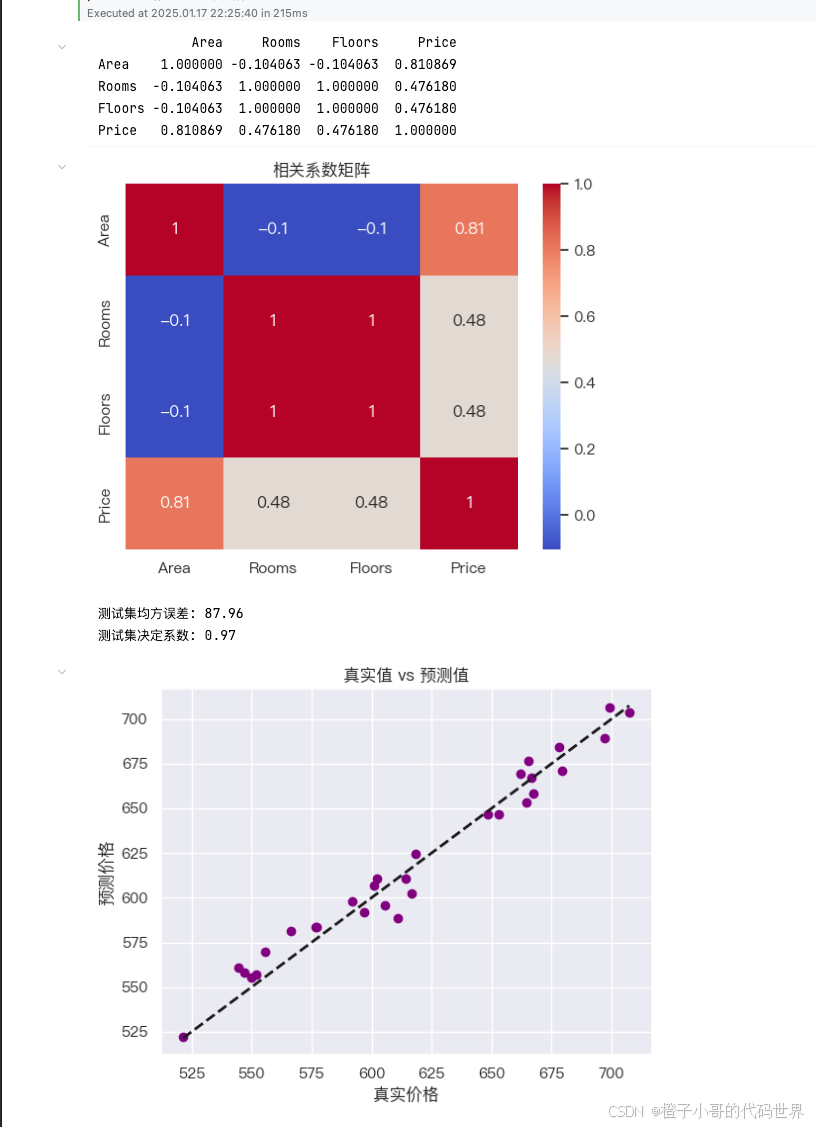
6. 如何解读热力图？

1. 颜色表示相关性：

• 红色：表示强正相关（相关系数接近 +1）。

• 蓝色：表示强负相关（相关系数接近 -1）。

• 白色或浅色：表示弱相关（相关系数接近 0）。

2. 特征间的相关性：

• 如果两个特征之间的相关性很高（|r| （绝对值）接近 1），说明它们可能包含重复信息（共线性）。

• 在这种情况下，可以删除其中一个特征，避免冗余影响模型的稳定性。

3. 目标变量 y 与特征 x 的相关性：

• 关注目标变量 y（如 total_bill）与其他特征的相关性，选择与 y 相关性高的特征（|r| 大）。

---

六、一些小提醒：相关≠因果，别轻易下结论

1. 相关不等于因果：

千万记住，我们只能说两个变量“相关”，并不能断定“消费金额”增加就一定会导致“小费”增加，因为因果关系的确认还需要更深入的实验或研究设计。

• 要想说“吃辣导致耐热提升”，还得做更严格的对照实验或用因果推断方法。只看到两者同时变化，可不一定谁影响谁。

2. 多变量共线性：

• 在多元回归模型中，若两个变量强相关，可能导致回归系数不稳定，要做变量筛选或正则化。

3. 非线性关系可能被忽略：

皮尔逊捕捉的是“线性”关联，如果两个变量呈抛物线关系（如“食物摄入量”与“幸福感”，少吃饿着急，多吃也腻歪），那么皮尔逊系数可能会给出一个“接近0”的结果，让你误以为两者不相关。这时就需要考虑非参数方法或先做曲线拟合分析。

• 如果散点图呈U形或其他曲线形状，皮尔逊相关系数可能显示“接近 0”，但其实有强关系，只是不是线性而已。

 4. 异常值的影响
  对于皮尔逊相关系数，极端异常值往往会极大地扭曲结果，建议在计算前先做必要的异常值探查与处理。

---

七、发展与未来：大数据时代的相关分析

• 现代数据不只是二维的“x vs. y”，而是高维、多模态的海量信息。我们在做探索性分析时，常用相关矩阵（Correlation Matrix）来看看各个特征之间的两两相关。

• 随着深度学习和复杂模型的出现，人们对于“相关分析”的需求更倾向可解释性：我们不仅想知道“强相关”，还想知道“为什么强相关”？这就衍生出因果分析、偏相关（partial correlation）等更深层次方法。

• 相关分析本身也在不断拓展：例如“距离相关”(distance correlation)、“信息熵相关”之类的非参数度量，旨在捕捉更广泛的依赖结构。不过在日常工作中，皮尔逊、Spearman 和 Kendall 仍是最常见也最实用的三驾马车。

---

八、总结：一把衡量线性关系的“万能小尺子”

通过以上循序渐进的分析，我们可以窥见相关分析在数据分析与建模中的重要地位。无论是皮尔逊还是斯皮尔曼、肯德尔，它们都只是我们探索数据关系的起点，后续还能结合可视化、假设检验、回归分析等方法进行更深入的研究。

• 皮尔逊：用于探究线性关系，适合连续型变量，要求分布尽量符合正态且对异常值敏感。
• 斯皮尔曼 / 肯德尔：基于排序思维，重点在于变量排名是否一致，适用于对分布要求不高、更抗噪的场合。

1. 重要地位：不管是学术研究还是企业数据分析，相关分析往往是第一步：先看看变量之间有无显著关联再做建模。

2. 灵活选择相关系数：根据分布、数据类型选对方法是关键；

3. 用好散点图和直方图：在做相关分析前，画画图总没错。

4. 记住：相关≠因果！ 这点可以算统计学的金科玉律之一了。

---

希望你在阅读后，能够幽默但又深刻地理解相关分析的内涵，并在实际数据项目中发挥威力。若你觉得这篇文章对你有所帮助，别忘了在点个赞、加个收藏，或把它分享给需要的小伙伴哦！

---

参考资料

• Pearson, K. (1895). Note on regression and inheritance in the case of two parents. Proceedings of the Royal Society of London.

• Spearman, C. (1904). The proof and measurement of association between two things. The American Journal of Psychology.

• Kendall, M. G. (1938). A new measure of rank correlation. Biometrika.

• 相关分析在 Python 中的常见函数：scipy.stats.pearsonr, scipy.stats.spearmanr, scipy.stats.kendalltau.

---

写在最后：数据科学之路漫漫，相关分析只是个入门法宝。愿我们都能时刻警惕“假象相关”，抓住“真相关”，在庞杂数据中找到那条“通往真理的直线”（或曲线）！

—— 全文完 ——

感谢阅读，期待你的点赞 + 关注 + 评论 + 收藏 + 转发，我们下期见！