数据结构 13.递归、回溯、分治、动态规划

一、 递归

https://blog.csdn.net/weixin_41725746/article/details/90241793.

二、回溯

1.回溯的概念

1.回溯算法就是一种有组织的系统最优化搜索技术，可以看作蛮力法穷举搜索的改进。回溯法常常可以避免搜索所有可能的解，所以它适用于求解组织数量较大的问题。

2.解空间树： 问题的解空间一般使用解空间树的方式来组织，树的根节点位于第1层，表示搜索的初始状态，依次向下排列。

3.解空间树的动态搜索： 在搜索至树中任一节点时，先判断该节点对应的部分是否是满足约束条件，或者是否超出目标函数的界，也就是判断该节点是否包含问题的最优解。如果肯定不包含，则跳过对该节点为根的子树的搜索，即所谓的剪枝；否则，进入该节点为根的子树，继续按照深度优先策略搜索。（这也是为什么回溯可以避免搜索所有的解）

4.在搜索过程中，通常采用两种策略避免无效搜索：
（1）用约束条件剪除得不到的可行解的子树
（2）用目标函数剪取得不到的最优解的子树
（这两种方式统称为：剪枝函数）

5.在用回溯法求解问题时，常常遇到两种典型的解空间树：
（1）子集树：但所有的问题是从n个元素的集合中找出满足某种性质的子集时，相应的解空间树成为子集树
（2）排列树：当所给出问题是确定n个元素满足某种性质的排列时，相应的解空间称为排列树。

6.回溯法的一般步骤：
（1）设置初始化的方案（给变量赋初始值，读入已知数据等）
（2）变换方式去试探，若全部试完侧转（7）
（3）判断此法是否成功（通过约束函数），不成功则转（2）
（4）试探成功则前进一步再试探
（5）正确方案还是未找到则转（2）
（6）以找到一种方案则记录并打印
（7）退回一步（回溯），若未退到头则转（2）
（8）已退到头则结束或打印无解

7.回溯法的优点在于其结构明确，可读性强，易于理解，而且通过对问题的分析可以大大提高运行效率。

2. 回溯相关练习

51.N皇后

https://leetcode-cn.com/problems/n-queens/
问题描述： n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

上图为8皇后问题的一种解法。
给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
示例：

输入: 4
输出: [
[".Q…", // 解法 1
“…Q”,
“Q…”,
“…Q.”],
["…Q.", // 解法 2
“Q…”,
“…Q”,
“.Q…”]
]
解释: 4 皇后问题存在两个不同的解法。

解题思路：
1、从1行开始，逐行扫描，避免了同行判断；
2、针对每一行的扫描，枚举列的全部可能；
3、剪枝的要点，判断同列、判断斜向左下和右上（x + y固定）、判断斜向右下和左上（x-y固定）；

代码实现

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        res = []
        s = "." * n
        def backtrack(i, tmp,col,z_diagonal,f_diagonal):
            if i == n:
                res.append(tmp)
                return 
            for j in range(n):
                if j not in col and i + j not in  z_diagonal and i - j not in f_diagonal:
                    backtrack(i+1,tmp + [s[:j] + "Q" + s[j+1:]], col | {
   j}, z_diagonal |{
   i + j} , f_diagonal |{
   i - j}  ) 
            
        backtrack(0,[],set(),set(),set())    
        return res

利用回溯算法求解 0-1 背包问题

问题描述： 给定N个物品和一个背包。物品i的重量是Wi,其价值位Vi ，背包的容量为C。问应该如何选择装入背包的物品，使得放入背包的物品的总价值为最大？
代码实现：

bestV=0
curW=0
curV=0
bestx=None
 
def backtrack(i):
    global bestV,curW,curV,x,bestx
    if i>=n:
        if bestV<curV:
            bestV=curV
            bestx=x[:]
    else:
        if curW+w[i]<=c:
            x[i]=True
            curW+=w[i]
            curV+=v[i]
            backtrack(i+1)
            curW-=w[i]
            curV-=v[i]
        x[i]=False
        backtrack(i+1)

        
if __name__=='__main__':
    n=5
    c=10
    w=[2,2,6,5,4]
    v=[6,3,5,4,6]
    x=[False for i in range(n)]
    backtrack(0)
    print(bestV) # 15
    print(bestx) # [True, True, False, False, True

三、分治

1.分治的概念

在计算机科学中，分治法是一种很重要的算法。字面上的解释是“分而治之”，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础，如排序算法(快速排序，归并排序)，傅立叶变换(快速傅立叶变换)……

2.分治算法的基本步骤

分治法在每一层递归上都有三个步骤：

step1 分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题；

step2 解决：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题

step3 合并：将各个子问题的解合并为原问题的解。

3.分治相关练习

利用分治算法求一组数据的逆序对个数

摘自：https://blog.csdn.net/contr4l_/article/details/80611675
题目描述： 对于一个序列a1,a2,a3…an, 若存在i,j，使得i<j且ai>aj，则称为一个逆序对

输入： 一个list对象
输出： list中逆序对数目

解题思路： 一个朴素的想法是这样的：依次遍历list中每一个元素，对每一个元素，查找其之后的每一个元素并与其比较，出现逆序对则计数+1，时间复杂度为O(n^2)——(n-1)+(n-2)+…+1。

但对于这个算法，实际上有隐含的条件被我们忽略了，例如当我们发现a2<a1时，那么对于和a2比较过的所有元素，与a2形成逆序对的所有元素实际上也与a1形成逆序对（除a2外），实际上时间复杂度可以精简到O(nlogn)。

我们可以换一个思路来考虑这个问题：对于一个a1<a2<a3…<an的有序序列，逆序对是为0的，那么我们实际上是要进行一个排序，当发现一次逆序，计数+1，而排序算法的最优解法为O(nlogn)

代码实现：

def Count(lst1, lst2,count): 
    i = 0
    j = 0
    res = []
    while i < len(lst1) and j < len(lst2):
        if lst1[i] <= lst2[j]:
            res.append(lst1[i])
            i += 1
        else:
            res.append(lst2[j])
            count += len(lst1)-i # 当右半部分的元素先于左半部分元素进入有序列表时，逆序对数量增加左半部分剩余的元素数
            j += 1
    res += lst1[i:]
    res += lst2[j:]
    return res,count
    
def InversionNum(lst):
    # 改写归并排序,在归并排序中，每当R部分元素先于L部分元素插入原列表时，逆序对数要加L剩余元素数
    if len(lst) == 1:
        return lst,0
    else:
        n = len(lst) // 2
        lst1,count1 = InversionNum(lst[0:n])
        lst2,count2 = InversionNum(lst[n:len(lst)])
        lst,count = Count(lst1,lst2,0)
        return lst,count1+count2+count
  
 
print(InversionNum([11,10,9,8,7,6,5,4,3,2,1]))  # 输出为：[1,2,3,4,5,6,7,8,9,10,11] 55

四、动态规划

摘自https://www.cnblogs.com/steven_oyj/archive/2010/05/22/1741374.html

1. 动态规划的概念

动态规划过程是：每次决策依赖于当前状态，又随即引起状态的转移。一个决策序列就是在变化的状态中产生出来的，所以，这种多阶段最优化决策解决问题的过程就称为动态规划。

2.基本思想与策略

基本思想与分治法类似，也是将待求解的问题分解为若干个子问题（阶段），按顺序求解子阶段，前一子问题的解，为后一子问题的求解提供了有用的信息。在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其他局部解。依次解决各子问题，最后一个子问题就是初始问题的解。

由于动态规划解决的问题多数有重叠子问题这个特点，为减少重复计算，对每一个子问题只解一次，将其不同阶段的不同状态保存在一个二维数组中。

与分治法最大的差别是： 适合于用动态规划法求解的问题，经分解后得到的子问题往往不是互相独立的（即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解）。

3. 适用的情况

能采用动态规划求解的问题的一般要具有3个性质：

• (1) 最优化原理：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理。
• (2) 无后效性：即某阶段状态一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关。
• （3）有重叠子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。（该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势）

4.动态规划相关练习

利用动态规划求解 0-1 背包问题

问题描述： 给定N个物品和一个背包。物品i的重量是Wi,其价值位Vi ，背包的容量为C。问应该如何选择装入背包的物品，使得放入背包的物品的总价值为最大？
解题思路：
①不超过背包容量，有：Σw[i]<=C (i表示第i件物品);
②对于“将前i件物品放入容量为j的背包中”这个子问题，现只考虑第i件物品放还是不放，如果放了的话，问题转换为“前i-1件物品放入剩下j-w[i]容量的背包中”，如果不放，问题转换为“前i-1件物品放入容量为j的背包中”。这两种情况的优者为当前问题的最优解；
③根据②的分析，得到如下递推公式：

其中，0<=i<=N,0<=j<=W.
④例子
5个物品的重量和价值分别为（5，12），（4，3），（7，10），（2，3），（6，6），背包容量15。

初始化表:

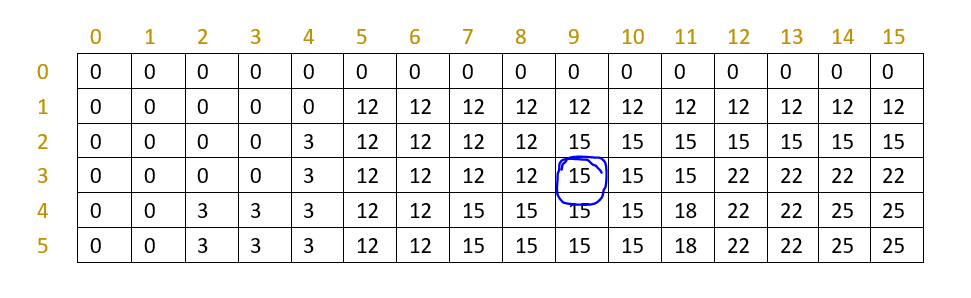
根据公式填表:

随便选一个来分析，比如上表圈中位置f[3][9]表示前3件物品放入容量为9的背包中，最高价值为15

• 15如何来的呢？
  考虑第三件物品放还是不放入背包，若放入背包f[3][9]=f[2][9-w[3]]+v[3]=f[2][2]+v[3]=0+10=10
  若不放入背包，f[3][9]=f[2][9]=15
  因为15>10，所有第三件物品不放入背包，前3件物品放入容量为9的背包得到的最高价值是15

代码实现：

def bag(n, c, w, v):
    """
    测试数据：
    n = 5  物品的数量，
    c = 15 书包能承受的重量，
    w = [5, 4, 7, 2, 6] 每个物品的重量，
    v = [12, 3, 10, 3, 6] 每个物品的价值
    """
    # 置零，表示初始状态
    value = [[0 for j in range(c + 1)] for i in range(n