双曲嵌入论文与代码实现——2. 方法与代码

本篇接上一篇：双曲嵌入论文与代码实现——1. 数据集介绍

1. 方法说明

首先学习相关的论文中的一些知识，并结合进行代码的编写。文中主要使用Poincaré embedding。

整体的空间为一个$d$维的开球：${\mathcal{B}}^d=\left\{\mathbf{x}\in {\mathbb{R}}^d\mid \Vert \mathbf{x}\Vert <1\right\}$，$\Vert \cdot \Vert$为欧几里得范数（Euclidean norm）。

黎曼度规张量（Riemannian metric tensor, $g_{\mathbf{x}}$）与欧几里得度规张量（$g^E$）之间的关系定义如下：
$$g_{\mathbf{x}}={\left(\frac{2}{1-\Vert \mathbf{x}{\Vert }^2}\right)}^2{g}^E\Rightarrow g^E=\frac{{\left(1-\Vert \mathbf{x}{\Vert }^2\right)}^2}{4}{g}_{\mathbf{x}}\text{\hspace{1em}(1)}$$
其中 $\mathbf{x}\in {\mathcal{B}}^d$，点$\mathbf{u},\mathbf{v}\in {\mathcal{B}}^d$ 之间的距离在此空间下的定义如下：
$$d(\mathbf{u},\mathbf{v})=\mathrm{arcosh}\left(1+2\frac{\Vert \mathbf{u}-\mathbf{v}{\Vert }^2}{\left(1-\Vert \mathbf{u}{\Vert }^2\right)\left(1-\Vert \mathbf{v}{\Vert }^2\right)}\right).$$

对应的python代码为：

def dist1(vec1, vec2): # eqn1 
    diff_vec = vec1 - vec2
    return 1 + 2 * norm(diff_vec) / ((1 - norm(vec1)) * (1 - norm(vec2)))

上述公式不仅可以表示出两个点之间的距离$\Vert \mathbf{u}-\mathbf{v}\Vert$，还能够衡量节点的层级属性$\Vert \mathbf{u}\Vert$, $\Vert \mathbf{v}\Vert$，此范数越接近$0$表示越接近根节点（根节点就是$0$），越接近$1$表示越接近开球的边界$\partial {\mathcal{B}}^d$。

损失函数

我们想要寻找最优的embedding，就需要构建一个损失函数，目标是使得相似词汇的embedding结果，尽可能接近，且层级越高（类别越大）的词越靠近中心。我们需要最小化这个损失函数，从而得到embedding的结果。

这里假设$n$个词的embeddings: Θ = { θ i } i = 1 n \Theta=\left\{\boldsymbol{\theta}_{i}\right\}_{i=1}^{n} Θ={θi​}i=1n​，我们的优化问题为：

$${\Theta }^{\prime }\leftarrow \underset{\Theta }{\mathrm{argmin}}\mathcal{L}(\Theta )\text{ s.t. }\forall {\mathbf{\theta }}_i\in \Theta :\Vert {\mathbf{\theta }}_i\Vert <1$$

由于是在半径为$1$的一个开球空间内进行优化，因此需要对embedding进行约束，限制范数小于$1$。

损失函数具体形式我们定义如下（注意，原始论文这里写错了，少了一个负号）：
$$\mathcal{L}(\Theta )=\sum _{(u,v)\in \mathcal{D}}-\log \frac{e^{-d(\mathbf{u},\mathbf{v})}}{{\sum }_{{\mathbf{v}}^{\prime }\in \mathcal{N}(u)}{e}^{-d\left(\mathbf{u},{\mathbf{v}}^{\prime }\right)}},$$

$(u,v)$ 为有邻边相连的正样本对，$(u,v^{\prime })$ 为负样本对（没有边连接），且 N ( u ) = { v ∣ ( u , v ) ∉ D } ∪ { u } \mathcal{N}(u)=\{v \mid(u, v) \notin \mathcal{D}\} \cup\{u\} N(u)={v∣(u,v)∈/​D}∪{u} 是关于 $u$ 的负样本集合（包括 $u$ ）。在训练中，针对每个正样本，我们随机采样$10$个负样本。

其实在传统的词嵌入中，我们也是用上述的损失函数，但距离选用的是余弦距离。

梯度下降

后面将使用梯度下降方法进行求解迭代。

$${\mathbf{\theta }}_{t+1}={\mathbf{\theta }}_t-{\eta }_t{\nabla }_R\mathcal{L}\left({\mathbf{\theta }}_t\right)$$

由于是将欧氏空间计算得到的梯度在黎曼空间中进行迭代，由上文的(1)式，我们有：

$${\mathbf{\theta }}_{t+1}={\mathbf{\theta }}_t-{\eta }_t\frac{{\left(1-{\Vert {\mathbf{\theta }}_t\Vert }^2\right)}^2}{4}{\nabla }_E\mathcal{L}\left({\mathbf{\theta }}_t\right)$$

梯度求解

这里关于欧氏空间的梯度 ${\nabla }_E=\frac{\partial \mathcal{L}(\mathbf{\theta })}{\partial d(\mathbf{\theta },\mathbf{x})}\frac{\partial d(\mathbf{\theta },\mathbf{x})}{\partial \mathbf{\theta }}$ 依赖于两个部分。

根据当前样本是属于正样本还是负样本可以很轻易求解出（具体求解结果可参考后面的代码，这里不进行表示）：
$$\frac{\partial \mathcal{L}(\mathbf{\theta })}{\partial d(\mathbf{\theta },\mathbf{x})}$$

下面考虑另一部分：
$$\frac{\partial d(\mathbf{\theta },\mathbf{x})}{\partial \mathbf{\theta }}$$

记 $\alpha =1-\Vert \mathbf{\theta }{\Vert }^2,\beta =1-\Vert \mathbf{x}{\Vert }^2$ 以及，
$$\gamma =1+\frac{2}{\alpha \beta }\Vert \mathbf{\theta }-\mathbf{x}{\Vert }^2$$
Poincaré distance 关于 $\mathbf{\theta }$ 的偏导可以求得
$$\frac{\partial d(\mathbf{\theta },\mathbf{x})}{\partial \mathbf{\theta }}=\frac{\partial \text{arcosh}\gamma }{\partial \gamma }\cdot \frac{\partial \gamma }{\partial \mathbf{\theta }}=\frac{4}{\alpha \beta \sqrt{{\gamma }^2-1}}\left(\frac{\Vert \mathbf{x}{\Vert }^2-2⟨\mathbf{\theta },\mathbf{x}⟩+1}{\alpha }\mathbf{\theta }-\mathbf{x}\right).$$

又由于限制：$\Vert \mathbf{\theta }\Vert <1$，因此在实际优化的过程中，为了避免embedding跑到开球外，我们通过投影约束，将embedding保持在Poincaré球内：
$$\mathrm{proj}(\mathbf{\theta })=\{\begin{array}{ll}\mathbf{\theta }/\Vert \mathbf{\theta }\Vert -\epsilon & \text{ if }\Vert \mathbf{\theta }\Vert \ge 1\\ \mathbf{\theta }& \text{ otherwise },\end{array}$$
$\epsilon$ 是为了保持数值的稳定而设置的常数，我们通常取 $\epsilon =10^{-5}$，因此总的迭代公式为：
$${\mathbf{\theta }}_{t+1}\leftarrow \mathrm{proj}\left({\mathbf{\theta }}_t-{\eta }_t\frac{{\left(1-{\Vert {\mathbf{\theta }}_t\Vert }^2\right)}^2}{4}{\nabla }_E\right)\text{. }$$

对应的更新函数在Python中设置如下：

# 范数计算
def norm(x):
    return np.dot(x, x)

# 距离函数对\theta求偏导
def compute_distance_gradients(theta, x, gamma):
    alpha = (1.0 - np.dot(theta, theta))
    norm_x = norm(x)
    beta = (1 - norm_x)
    c_ = 4.0 / (alpha * beta * sqrt(gamma ** 2 - 1))
    return c_ * ((norm_x - 2 * np.dot(theta, x) + 1) / alpha * theta - x)

# 更新公式
def update(emb, grad, lr): 
    c_ = (1 - norm(emb)) ** 2 / 4
    upd =  lr * c_ * grad
    emb = emb - upd
    if (norm(emb) >= 1):
        emb = emb / sqrt(norm(emb)) - eps
    return emb

至此，我们就可以开始写一个完整的训练过程了。在这之前，再补充一个绘图函数（可以看embedding的实际训练情况）：

def plotall(ii):
    fig = plt.figure(figsize=(10, 10))
    # 绘制所有节点
    for a in emb:
        plt.plot(emb[a][0], emb[a][1], marker = 'o', color = [levelOfNode[a]/(last_level+1),levelOfNode[a]/(last_level+1),levelOfNode[a]/(last_level+1)])
    for a in network:
        for b in network[a]:
            plt.plot([emb[a][0], emb[b][0]], [emb[a][1], emb[b][1]], color = [levelOfNode[a]/(last_level+1),levelOfNode[a]/(last_level+1),levelOfNode[a]/(last_level+1)])
            circle = plt.Circle((0, 0), 1, color='y', fill=False)
            plt.gcf().gca().add_artist(circle)
    plt.xlim(-1, 1)
    plt.ylim(-1, 1)
    fig.savefig('~/GitHub/hyperE/fig/' + str(last_level) + '_' + str(ii) + '.png', dpi = 200)

2. 代码训练过程

首先初始化embeddings，这里按照论文中写的，用$(-0.001,0.001)$间的均匀分布进行随机初始化：

emb = {}
for node in levelOfNode:
    emb[node] = np.random.uniform(low = -0.001, high = 0.001, size = (2, ))

下面设置学习率等参数：

vocab = list(emb.keys())
eps = 1e-5    
lr = 0.1       # 学习率
num_negs = 10  # 负样本个数

接下来开始正式迭代，具体每一行的含义均在注释中有进行说明：

# 绘制初始化权重
plotall("init")

for epoch in range(1000):
    loss = []
    random.shuffle(vocab)
    
    # 下面需要抽取不同的样本：pos2 与 pos1 相关；negs 不与 pos1 相关
    for pos1 in vocab:
        if not network[pos1]: # 叶子节点则不进行训练
            continue
        pos2 = random.choice(network[pos1]) # 随机选取与pos1相关的节点pos2
        dist_pos_ = dist1(emb[pos1], emb[pos2]) # 保留中间变量gamma，加速计算
        dist_pos = np.arccosh(dist_pos_) # 计算pos1与pos2之间的距离
        
        # 下面抽取负样本组（不与pos1相关的样本组）
        negs = [[pos1, pos1]]
        dist_negs_ = [1] 
        dist_negs = [0]
        
        while (len(negs) < num_negs):
            neg = random.choice(vocab)
            
            # 保证负样本neg与pos1没有边相连接
            if not (neg in network[pos1] or pos1 in network[neg] or neg == pos1): 
                dist_neg_ = dist1(emb[pos1], emb[neg])
                dist_neg = np.arccosh(dist_neg_)
                negs.append([pos1, neg])
                dist_negs_.append(dist_neg_) # 保存中间变量gamma，加速计算
                dist_negs.append(dist_neg)
        
        # 针对一个样本的损失
        loss_neg = 0.0
        for dist_neg in dist_negs:
            loss_neg += exp(-1 * dist_neg)
        loss.append(dist_pos + log(loss_neg))
        
        # 损失函数 对 正样本对 距离 d(u, v) 的导数
        grad_L_pos = -1
        
        # 损失函数 对 负样本对 距离 d(u, v') 的导数
        grad_L_negs = []
        for dist_neg in dist_negs:
            grad_L_negs.append(exp(-dist_neg) / loss_neg)
            
        # 计算正样本对中两个样本的embedding的更新方向
        grad_pos1 = grad_L_pos * compute_distance_gradients(emb[pos1], emb[pos2], dist_pos_)
        grad_pos2 = grad_L_pos * compute_distance_gradients(emb[pos2], emb[pos1], dist_pos_)
        
        # 计算负样本对中所有样本的embedding的更新方向
        grad_negs_final = []
        for (grad_L_neg, neg, dist_neg_) in zip(grad_L_negs[1:], negs[1:], dist_negs_[1:]):
            grad_neg0 = grad_L_neg * compute_distance_gradients(emb[neg[0]], emb[neg[1]], dist_neg_)
            grad_neg1 = grad_L_neg * compute_distance_gradients(emb[neg[1]], emb[neg[0]], dist_neg_)
            grad_negs_final.append([grad_neg0, grad_neg1])
            
        # 更新embeddings
        emb[pos1] = update(emb[pos1], -grad_pos1, lr)
        emb[pos2] = update(emb[pos2], -grad_pos2, lr)
        for (neg, grad_neg) in zip(negs, grad_negs_final):
            emb[neg[0]] = update(emb[neg[0]], -grad_neg[0], lr)
            emb[neg[1]] = update(emb[neg[1]], -grad_neg[1], lr)
    
    # 输出损失
    if ((epoch) % 10 == 0):
        print(epoch + 1, "---Loss: ", sum(loss))
        
    # 绘制二维embeddings
    if ((epoch) % 100 == 0):
        plotall(epoch + 1)

3. 结果表现

结果如下所示（与论文有些不一致）：

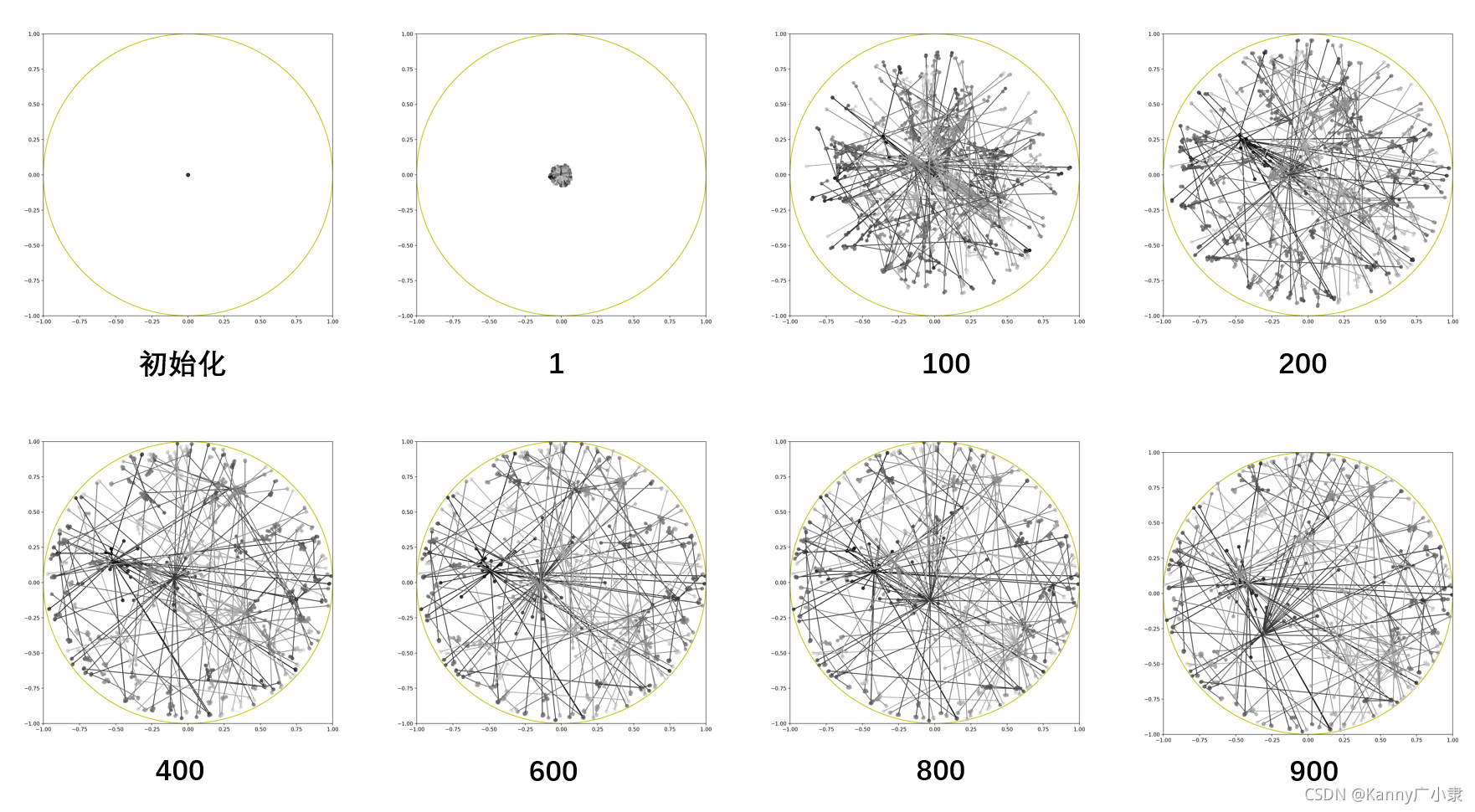
实际上应该还是有效的，有些团都能聚合在一起，下面是一个随机训练的结果（可以看出非常混乱）：

其他参考资料

1. Poincaré Embeddings for Learning Hierarchical Representations
2. Implementing Poincaré Embeddings
3. models.poincare – Train and use Poincare embeddings
4. How to make a graph on Python describing WordNet’s synsets (NLTK)
5. networkx.drawing.nx_pylab.draw_networkx