【FOC进阶日记】实战篇 ① FOC与SVPWM详解

关注+星标公众号，不错过精彩内容

作者 | 量子君
微信公众号 | 极客工作室

---

【FOC进阶日记】专栏目录
第一章 实战篇 ① FOC与SVPWM详解
第二章 实战篇 ② 自发电控制算法

---

前言

本专栏专注分享在 FOC（基于磁场定向控制的 BLDC 电机控制器）方面的学习过程和心得体会。包括 FOC 控制算法时的实验成果和代码实现，和一些电机控制方面的基础知识和实用技巧。通过这些内容的分享，希望能够帮助更多的人理解和掌握 FOC 控制算法，让大家能够更加轻松地开发和控制电机。

本章介绍了电机原理、无刷电机六步换相、获取转子角度、驱动电路、电压空间矢量、FOC原理、算法等学习FOC需要的所有知识点详解。看完本文会对FOC有一个很详细的了解，多次观看，细细品味一定会对学习FOC有一个质的提升！

---

一、FOC简介

FOC (Field-Oriented Control)，直译是磁场定向控制，也被称作矢量控制(VC，VectorControl)，是目前直流无刷电机 （BLDC）和永磁同步电机（PMSM）高效控制的最优方法之。FOC旨在通过精确地控制磁场大小与方向，使得电机的运动转矩平稳、噪声小、效率高，并且具有高速的动态响应。

简单来说就是，FOC是一种对无刷电机的驱动控制方法，它可以让我们对无刷电机进行“像素级”控制，实现很多传统电机控制方法所无法达到的效果。

二、电机原理

2.1 电机分类

FOC主要应用于永磁无刷直流电动机：

1. 方波驱动电机，也即无刷直流电机(BLDC)；
2. 正弦波驱动电机：也即永磁同步电机(PMSM)。

BLDC和PMSM相同点：

1. 它们的电动机都是永磁电动机，转子由永磁体组成基本结构，定子安放有多相交流绕组；
2. 都是由永久磁铁转子和定子的交流电流相互作用产生电机的转矩；
3. 在绕组中的定子电流必须与转子位置反馈同步；
4. 转子位置反馈信号可以来自转子位置传感器，或者像在一些无传感器控制方式那样通过检侧电机相绕组的反电动势等方法得到。

BLDC和PMSM不同点：

1. 反电势不同， PMSM具有正弦波反电势，而BLDC具有梯形波反电势；
2. 定子绕组分布不同， PMSM采用短距分布绕组，有时也采用分数槽或正弦绕组，以进一步减小纹波转矩；而BLDC采用整距集中绕组。
3. 运行电流不同，为产生恒定电磁转矩，PMSM为正弦波定子电流； BLDC为矩形波电流。
4. 永磁体形状不同， PMSM永磁体形状呈抛物线形，在气隙中产生的磁密尽量呈正弦波分布；BLDC永磁体形状呈瓦片形，在气隙中产生的磁密呈梯形波分布。
5. 运行方式不同， PMSM采用三相同时工作，每相电流相差120°电角度，要求有位置传感器。BLDC采用绕组两两导通，每相导通120°电角度，每60°电角度换相，只需要换相点位置检测。正是这些不同之处，使得在对PMSM和BLDCM的控制方法、控制策略和控制电路上有很大差别。

简单地说，BLDC由于反电动势接近梯形波，所以肯定是会有上面说的抖动问题的，但是转一圈抖6下太明显了，如果我增加电机槽、极对数(也就是磁铁对数)，那以前是360度里面抖6下，现在变成120度里面抖6下，甚至更小，这样“颗粒感”不就变得更小了嘛? 实际中买到的BLDC电机基本都是多极对的(比如下图)，原理跟之前的分析是一样的，出来的都是三相信号(图中的三根线)，可以自己进行类推。BLDC也可以结合抗齿槽算法的FOC进行力矩补偿实现平滑控制。

而另一方面，为什么我们非得用方波这种不平滑的波来驱动电机呢，用正弦波它不香吗? 是的，这就是PMSM解决问题的方式，由于PMSM的反电动势被设计为正弦波的形状，我们用软件和算法结合PWM技术将方波转变成等效的SPWM正弦波或者SVPWM马鞍波，再来驱动电机，结果美滋滋，控制效果很理想。当然为了产生更好的波形、更好的旋转磁场，驱动器、控制算法就变得非常复杂，这也是FOC的实现原理。

2.2 基础知识

1. 左手定则：用于判断导线在磁场中受力的方向: 伸开左手，使拇指与其他四指垂直且在一个平面内，让磁感线从手心流入，四指指向电流方向，大拇指指向的就是安培力方向 (即导体受力方向)。
   
2. 右手定则
   伸开右手，使大拇指跟其余四个手指垂直并且都跟手掌在一个平面内，把右手放入磁场中，让磁感线垂直穿入手心，大拇指指向导体运动方向，则其余四指指向感生电动势的方向。也就是切割磁感线的导体会产生反电动势，实际上通过反电动势定位转子位置也是普通无感电调工作的基础原理之一。
   
3. 安培定则（右手螺旋定则）
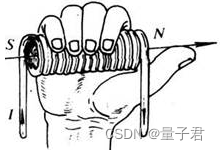
   用于判断通电线圈判断极性:用右手握螺线管，让四指弯向螺线管中电流方向，大拇指所指的那端就是螺线管的N极。直线电流的磁场的话，大拇指指向电流方向，另外四指弯曲指的方向为磁感线的方向。
   
4. PWM（脉冲宽度调试）
   本质是利用面积等效原理来改变波形的有效值。举个例子，一个电灯只有开和关两个状态，那么要怎么让它实现50%亮度的效果的呢? 只需要让它在一半时间开，一半时间关，交替执行这两个动作只要频率足够高，在人眼(低通滤波器)看起来就是50%亮度的样子了。而其中高电平占一个开关周期的比例，就叫做占空比。利用PWM可以实现使用离散的开关量来模拟连续的电压值。

2.3 无刷电机原理

考察下图情况中的直流电机基本模型，根据磁极异性相吸同性相斥的原理，中间永磁体在两侧电磁铁的作用下会被施加一个力矩并发生旋转，这就是电机驱动的基本原理。

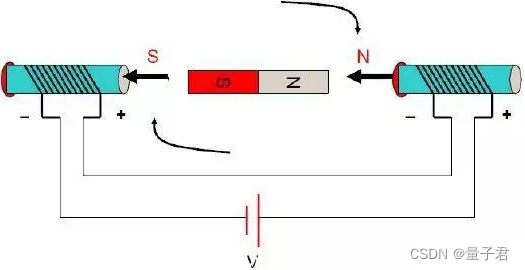
当两个电磁铁呈直角时，力矩(力矩在物理学里是指作用力使物体绕着转动轴或支点转动的趋向)最大(可以简单的认为相互作用力最大)。

对于简化的无刷电机来说，以三相二极内转子电机为例，定子的三相绕组有星形联结方式和三角联结方式，而三相星形联结的二二导通方式最为常用，这里就用该模型来做个简单分析：

如上图所示，无刷电机三相的连接方式是每一相引出导线的一头，而另一头和其他相两两相连。这个情况下假如我们对A、B极分别施加正电压和负电压，那么由右手螺旋定则可以判断出线圈磁极的方向如下图：

当中间的转子处于和CO（O为中心点）连线平行的时候收到的力矩最大，磁铁会受到A、B两个磁极一推一拉的作用，直到旋转到与AB连线平行的且磁铁内部磁力线方向和AB间磁力线方向一致的时候，受合力矩为0且稳定，也就是上图中右边的状态。换句话说，AB相通电会让转子努力转到上图中右边的状态。至于C文时暂时不起作用。

同理，我们下一阶段换成AC相通电，这时候转子会倾向于转到下图右边水平的角度：

以此类推，可以得到每个通电状态下转子的角度，就是下图中的6个状态，每个状态相隔60度，6个过程即完成了完整的转动，共进行了6次换相：

我们只需要像步进电机那样不断的重复这六步换向就可以让无刷电机转动起来。但是并不是换向越快电机转的就越快。当转子处于特定位置时才去触发换向操作，换向是被动换向，想要提高转速一定是要提高电流，让定子产生的磁场更强，让转子更快的达到目标点然后触发换向电机。整个连续动作如下动图所示，这也就是所谓的“六步换相法”。

驱动器就是完成换向操作的。这也是无刷电机和有刷电机最大的区别，即不像有刷电机的机械换向，无刷电机是通过电子换向来驱动转子不断地转动，电机的电压和KV值决定了电机转速，而电机的转速就决定了换向的频率。至于FOC则是解决什么时候怎么知道该换到哪个供电相? 如何产生更平滑的换向电压? 如何提高电源的利用效率这些问题的。

2.4 获取转子角度

检测当前角度有以下三种方式：

1. 通过安装编码器来计算出当前角度。
2. 通过安装霍尔元件计算当前角度。
3. 通过检测电流来计算当前角度。

2.4.1 编码器方式获取电机当前角度

编码器方式分为两种，增量式编码器和绝对式编码器：

1. 增量式编码器： 每次启动之气都需要做一次校准，而且为了防止单片机性能问题导致脉冲丢失，还需要对编码器每圈校准一次。因此经常使用ABZ三轴编码器，AB输出正交信号，Z轴输出中断。
2. 绝对式编码器： 只需要在出厂之前做一次校准，之后如果没有拆机便不需要校准，通讯方式一般是SPI和IIC，需要考虑通讯时间对系统的影响。

为什么要对编码器进行校准？ 因为我们无法保证在安装的时候让编码器的0°（机械角度）刚好对应电机转子的0°（电气角度：一般情况下默认电气角度的0度为指向a相绕组的方向）注意电气角度=机械角度*电机极对数，其中电机极对数等于转子磁极对数 (因为当只有一对磁极时转子转动机械角度360度回到初始状态，当有两对磁极时转子只需要转动180度即可回到初始状态。)

2.4.2 霍尔元件获取电机当前角度

霍尔元件有两种安装方式，互差120°和互差60°两种方式，因此在使用之前要判断电机是那种安装方式。

1. 互差120°时，霍尔电平和转子角度之间的对应关系如下表所示：
   
   

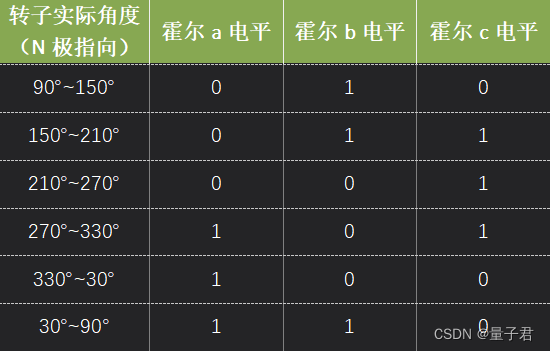
2. 互差60°时，霍尔电平和转子角度之间的对应关系如下表所示：
   
   

2.4.3 检测电流获取电机当前角度

由于电机旋转过程中产生的电流理想波形如下图，我们便可以根据采集到的电流就判断出电机当前的角度在哪个范围。 具体分析在FOC控制方法中讲解。

2.5 驱动电路

无刷电机的驱动电路主要使用三相逆变电路来实现，如下图：

所谓逆变电路，即把直流电变换为交流电，或者简单点说就是一个可以产生不同电流流向的电路通过前面的电机模型分析我们也可以看出，对于无刷电机的驱动是需要在不同时刻施加不同方向的电压(电流)的，因此需要逆变电路。

而逆变电路具体的实现则一般是采用半桥MOS电路来制作的。半桥电路的原型如下，其实很简单，就是两个MOS管组成的上桥臂和下桥臂，中间引出一条输出线：

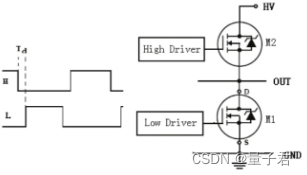
用3个半桥电路就可以组合成三相逆变电路，每个半桥引出的一根输出线跟无刷电机的一根相线相连，就完成了最基本的无刷驱动电路。

原理方面，MOS管可以看作电压控制的高速电子开关，在MOS管的栅极 (上图中的High Drive和Low Drive)施加高电平或者低电平，就可以控制MOS源极和漏极的导通或者关闭。比如在下图中，我们打开第一组半桥的上桥臂、第二组和第三组半桥的下桥臂(其余的关闭)，那么就可以让电流从电源正极流过电机的a相，流经b、c相，然后回到电源负极。

2.6 电压空间矢量

空间电压矢量是我们在控制电机过程中虚拟出来的一个矢量，既然是矢量，自然是有大小和方向的，那么它的大小和方向是什么呢？如果我们规定指向中心的方向为正，反之为负，那么此时我们可以画出下图中的三个电压矢量，以及它们的合成电压矢量（绿色箭头表示的矢量）：

也就是说，这个状态下我们可以认为电机中存在一个矢量$\vec{U}$表征的电压（电流）；然后根据右手螺旋定则，可以判断出磁场的磁力线方向，也是和矢量$\vec{U}$​一致的。所以最终产生的磁场方向汇总如下：

因为转子永磁体会旋转到内部磁力线和外部磁场方向一致，所以这个矢量​其实就可以表征我们希望转子旋转到的方向，也即所需要生成的磁场方向了。而这个矢量是会不断在空间中旋转的，它的幅值不变，为相电压峰值U(母线电压，也就是电源电压)​，且以角速度ω = 2Πf匀速旋转。SVPWM算法的目的，就是使用三相桥的开关状态把在空间中旋转的​矢量表示出来，我们把这个矢量称为空间电压矢量。

用数学公式来表示的话就是：
$$\{\begin{array}{l}Ua(t)=U\ast cos(2\Pi ft)\\ \\ Ub(t)=U\ast cos(2\Pi ft-\frac{2\Pi }{3})\\ \\ Uc(t)=U\ast cos(2\Pi ft+\frac{2\Pi }{3})\end{array}$$为了研究各相上下桥臂不同开关组合时逆变器输出的空间电压矢量，我们定义开关函数S_(x)​(x∈a，b，c)​为：
$$S(x)=\{\begin{array}{l}1，上桥臂导通\\ 0，下桥臂导通\end{array}$$S_(x)​的全部可能组合共有8个，包括 6个非零矢量U₁(001)、U₂(010)、U₃(011)、U₄(100)、U₅(101)、U₆(110)，和两个零矢量U₀(000)、U₇(111)。当零矢量状态下电机三相间电压都为0不产生转矩（不考虑反电动势）。

如图空间电压矢量，它们的端点组成了一个正六边形，同时把平面划分成了六个扇区。

当电磁铁的方向和转子(永久磁铁)的方向呈90度的时候，力矩最大。此时转子会向着电磁铁的方向旋转，此时若转子受到牵引转动了θ角，与此同时电磁铁也按照同方向转动了θ角，那么电磁铁的方向始终和转子的方向垂直，这样转子就会不断的进行旋转了并且力矩始终是最大的，这就好比下图：毛驴一直跟着胡萝卜的位置进行转动，但是毛驴和胡萝卜的位置确不会被改变

现在我们已经知道我们需要的是一个旋转任意角度的磁场并且大小可控，但是由上面描述三相线圈只能生成6个方向的电压矢量(电压矢量的方向和磁场方向相同)，那么如何根据这6个电压矢量合成任意角度的电压矢量(磁场方向)呢？这就是SVPWM要干的事情了。

三、FOC控制原理

3.1 FOC简介

磁场定向控制（Field-Oriented Control，FOC）系统的基本思想是：

通过坐标变换，在按转子磁场定向同步旋转坐标系中，得到等效的直流电动机模型；
仿照直流电动机的控制方法控制电磁转矩与磁链。
然后将转子磁链定向坐标系中的控制量反变换得到三相坐标系的对应量，以实施控制。

具体流程如下图所示：

如上图是以电流闭环控制为例的，也就是让电机始终产生一个恒定的力矩（也就是恒定的电流，因为力矩和电流成正比）。可以看到控制器的输入是最左边的I_{q_ref​}和I_{d_ref​​}，两个变量经过PID控制器进行反馈调节，其中还涉及到几个变换模块，有Park变换和Clark变换；最后通过前面提到的SVPWM模块作用到三相逆变器上进而控制电机；而PID控制器的反馈量，是对电机输出电流的采样值。

FOC控制的整个过程：

 1.对电机三相电流进行采样得到Ia、Ib、Ic。
 2.将Ia、Ib、Ic经过Clark变换得到​Iα、Iβ。
 3.将​Iα、Iβ​经过Park变换得到Iq、Id。
 4.计算​Iq、Id和其设定值Iq_ref、Id_ref​的误差。
 5.将上述误差输入两个PID（只用到PI）控制器，得到输出的控制电压​Uq、Ud。
 6.将​Uq、Ud进行反Park变换得到​Uα、Uβ。
 7.用​Uα、Uβ​合成电压空间矢量，输入SVPWM模块进行调制，输出该时刻三个半桥的状态编码值。
 8.按照前面输出的编码值控制三相逆变器的MOS管开关以驱动电机。
 9.循环上述步骤。

FOC最重要的原则：

按转子磁场定向，即保持转子磁链旋转矢量始终与dq坐标系下的d轴重合，q轴正交。
通过按转子磁场定向，将定子电流解耦为了励磁分量 id和转矩分量 iq。
通过电流 id实现对转子磁链的控制，电流 iq实现对电磁转矩的控制，类比于直流电机的控制。
对于表贴式永磁同步电机SPM，一般设置励磁分量id=0，定子电流全部用于产生电磁转矩。

FOC最主要的任务：

通过不停的观测转子角度，实现转子磁链定向。
即保持转子磁链旋转矢量始终与dq坐标系下的d轴重合，q轴正交，dq坐标轴同转子磁链同步旋转。

3.2 Clark变换和Park变换

3.2.1 Clark变换

在对电机的三个相电流进行采样时，这一步会使用串联的采样电阻（Shunt）进行电流采样。由于电机工作的电流一般很大，所以采样电阻的阻值非常小，甚至和导线的电阻接近了，因而实际的采样电路PCB设计的时候还有一些讲究，比如使用开尔文接法(Kelvin connections)。

我们知道采集到的三相电流Ia、Ib、Ic的波形如图：

其三相坐标系​如图：

由于采集到的三相电流Ia、Ib、Ic这三个基向量是非正交的，通过基变换可以将其正交化为一个直角坐标系，我们把新的直角坐标系命名为​α-β坐标系，实际上就是个做了一个坐标轴投影计算，变换过程如下：$$\left[\begin{array}{c}I\alpha \\ I\beta \\ I\gamma \end{array}\right]=\frac{2}{3}\left[\begin{array}{ccc}cos0& cos\frac{2\Pi }{3}& cos(-\frac{2\Pi }{3})\\ & & \\ sin0& sin\frac{2\Pi }{3}& sin(-\frac{2\Pi }{3})\\ & & \\ \frac{1}{2}& \frac{1}{2}& \frac{1}{2}\end{array}\right]\left[\begin{array}{c}Ia\\ Ib\\ Ic\end{array}\right]$$$$\left[\begin{array}{c}I\alpha \\ I\beta \\ I\gamma \end{array}\right]=\frac{2}{3}\left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ & & \\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\\ & & \\ \frac{1}{2}& \frac{1}{2}& \frac{1}{2}\end{array}\right]\left[\begin{array}{c}Ia\\ Ib\\ Ic\end{array}\right]$$$$\left[\begin{array}{c}I\alpha \\ I\beta \\ I\gamma \end{array}\right]=\frac{2}{3}\left[\begin{array}{ccc}\frac{2}{3}& -\frac{1}{3}& -\frac{1}{3}\\ & & \\ 0& \frac{1}{\sqrt{3}}& -\frac{1}{\sqrt{3}}\\ & & \\ \frac{1}{3}& \frac{1}{3}& \frac{1}{3}\end{array}\right]\left[\begin{array}{c}Ia\\ Ib\\ Ic\end{array}\right]$$可得I_α、I_β​、I_γ​的值：$$\{\begin{array}{l}I\alpha =\frac{2}{3}Ia-\frac{1}{3}\end{array}$$