在科研生涯中,导师要求做一个区分器,奈何只能得到一个类别的数据集,百思不得其解,多方查找,了解one class classification,随在此对此类问题进行详细介绍。
分类问题,例如二分类和多分类,由于多分类问题都可以解体成多个二分类问题,所以,一般来说,二分类问题被看做是基本的分类问题,在这里就拿二分类问题为例。在一个二分类问题中,元素被分成两个类, 和
,被分别标记成+1和-1,或者称为正类和负类,也就是训练集合中的每一个元素
分属于集合
。分类问题的目标是要从训练集合中学习到一个函数
y = f \left( x \right) ,这个函数能够对于一个新的给定的元素x进行预测出其所属类别,而且要尽可能准确。
在二分类里,理想情况下,需要要求训练集中的每类元素的数量巨大且几乎相等,即使在现实世界中,会出现正负类样本失衡的情况,所幸,众多策略已经被提出来解决此类问题,有点偏题,不多赘述。但是如果训练集中仅仅只有一类数据,那么要如何测试新的数据呢?并如何判断它是否与训练数据相似?这就引入了 one class classification。在one-class classification中,仅仅只有一类的信息是可以用于训练,其他类别的(总称为outlier)信息是缺失的,也就是区分两个类别的边界线是通过仅有的一类数据的信息学习得到的。
举例说明,假设有一个apple-pear的数据集,每个元素包含有两个特征,宽度width和重量weight,所属类别为苹果或梨。那么训练数据集的每一个元素可以表示成一个2维特征空间里的一个点,下图中的红色星星点表示苹果,蓝色加号点表示梨。虚线圈表示整个数据集。图1中的黑色实线将苹果和梨完美地进行区分,在二分类里面,类别仅仅包括苹果和梨,那么所有的元素要么是苹果要么是梨,不可能是其他类别。对于one class classification,将apple-pear看做一个整体,为一个类apple-pear,其他的不在这个数据集范围内(图1虚线圈)的则属于outlier,outlier包含非(苹果和梨)的其他所有类别。也就是说对于一个新的元素,假如它在虚线圈中,则说明这个元素的类别为apple-pear,加入处于虚线圈外,则说明这个元素的类别既不是苹果也不是梨,至于是什么,不清楚。
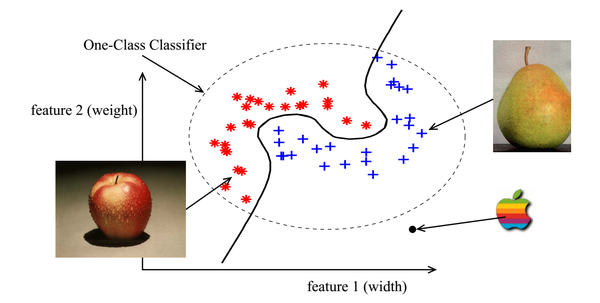
support vector data description(SVDD)
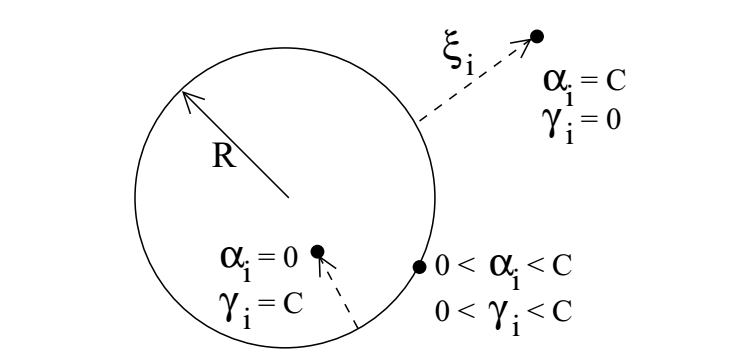
在one-calss classification中,边界应该全方位包围数据,我们定义一个对数据封闭的边界模型 :一个超球面。定义这个超球面的中心点为 a ,半径为R,我们需要这个超平面能够包含所有的训练数据,那么也就是说训练集的经验风险损失(empirical error)为0,那也就是说所有数据所有元素
x_{i} 到超球面的中心a的距离应该严格小于半径R
。但是为了使得模型更加健壮,也就是说允许一部分outlier存在一定概率被错认为数据集中的元素,那么经验损失就不必须是为0. 引入一个松弛变量slack variable
,则损失函数则既包含经验风险,还包含结构风险,如下所示:
限制条件为:
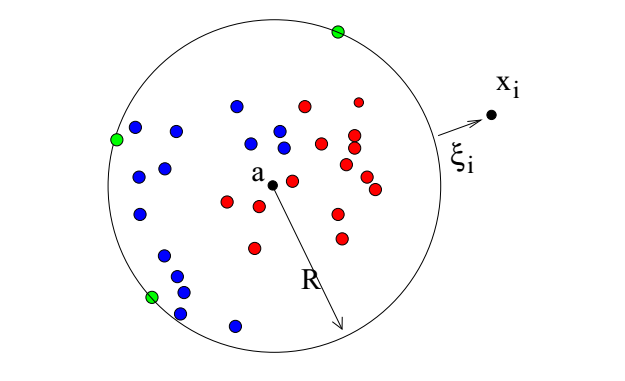
引入拉格朗日乘子Lagrange multiplier,构建拉格朗日函数为:
拉格朗日乘子 和
对每一个变量进行求导,可得到:
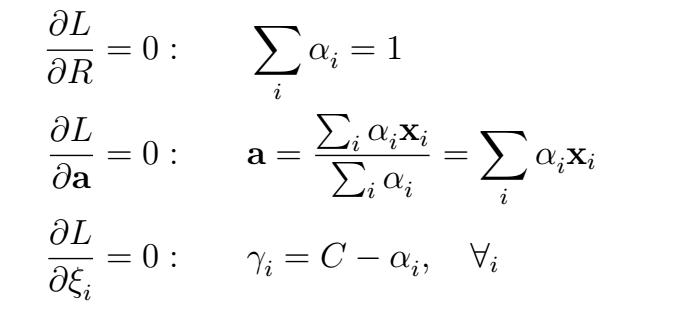
由于 ,而且
,由此推出一个新的限制条件
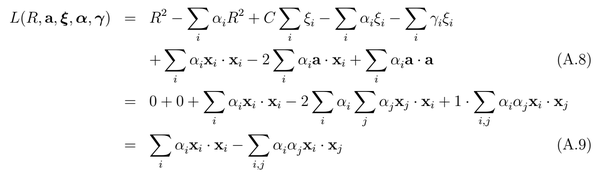
所以经过上述的推导,最后的损失函数带上限制条件如下面的公式所示:
v-support vector classifier
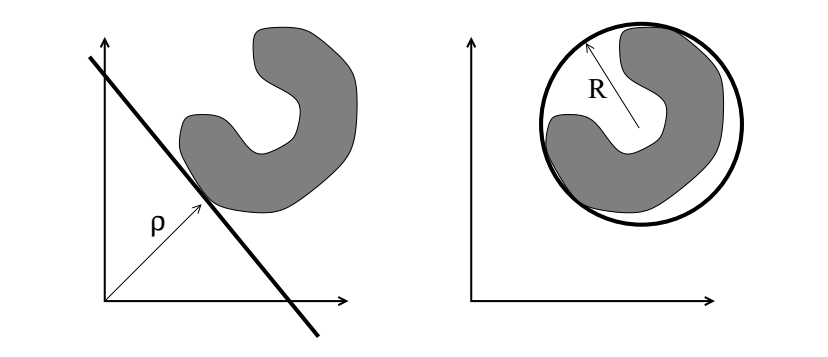
上述的SVDD算法定义了一个包围数据的超球面,形成一个封闭的边界。而v-SVC的基本思想是放置一个能够将数据dataset和原点origin用最大间隔值(maximal margin)分开的超平面,如图4所示。定义超平面为 \omega ,数据为
x_{i} ,最大间隔为
\rho ,超平面
\omega 将数据
x_{i} 和原点以最大间隔
\rho 分隔,公式表示为:
对于要最小化的目标函数,则定义为:
其中正则化参数 是一个用户定义的参数,指示能够接受的数据的百分比。这也是v-SVC的由来。
对于一个新的测试数据 z ,判别函数为:
v-SVC 在二分类SVM的基础上就很好理解,对支持向量机不熟悉的,请移步:逻辑回归LR vs 支持向量机
参考文献:
[1] . one class classification























 8159
8159











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










