1.复合函数的求导（由外到内）
[ f ( △ ) ] ′ = f ′ ( △ ) ⋅ △ [f(△)]^′ = f^′(△)·△ [f(△)]′=f′(△)⋅△
例1：f(x)=sin2x，求
f
′
(
x
)
的导数
f^′(x)的导数
f′(x)的导数
解：
f
′
(
x
)
=
c
o
s
2
x
⋅
2
=
2
⋅
c
o
s
2
x
f^′(x)=cos2x·2=2·cos2x
f′(x)=cos2x⋅2=2⋅cos2x
记住下面这个公式
ln
(
x
+
x
2
+
1
)
′
=
1
x
2
+
1
\ln (x+\sqrt {x^2+1})^′= \frac{1}{\sqrt {x^2+1}}
ln(x+x2+1)′=x2+11
1.幂指函数的求导
什么叫幂指函数：
上面和下面都有关于x的自变量
f(x)=
u
(
x
)
v
(
x
)
=
=
=
>
(
u
v
)
u(x)^{v(x)} ===>(u^v)
u(x)v(x)===>(uv)
例： s i n x x sin x^{x} sinxx就是幂指函数
求导步骤：
①变形：
△
=
e
l
n
△
=
=
=
>
u
v
=
e
l
n
u
v
=
e
v
⋅
l
n
u
△=e^{ln △} ===>u^v=e^{ln u^{v}}=e^{v·ln u}
△=eln△===>uv=elnuv=ev⋅lnu
② ( e v ⋅ ln u ) ′ = e v ⋅ ln u ⋅ ( v ⋅ ln u ) ′ = e v ⋅ ln u ⋅ ( v ′ ⋅ ln u + v ⋅ u ′ u ) = u v ( v ′ ⋅ ln u + v ⋅ u ′ u ) (e^{v·\ln u})^′=e^{v·\ln u}·(v·\ln u)^′=e^{v·\ln u}·(v^′·\ln u+v· \frac{u^′}{u})=u^v(v^′·\ln u+v· \frac{u^′}{u}) (ev⋅lnu)′=ev⋅lnu⋅(v⋅lnu)′=ev⋅lnu⋅(v′⋅lnu+v⋅uu′)=uv(v′⋅lnu+v⋅uu′) ，这里u是复合函数
例：
y
=
x
x
y=x^x
y=xx的导数。
解：
y
′
=
x
x
(
ln
x
+
1
)
y^′=x^x(\ln x+1)
y′=xx(lnx+1)
3对数求导法
ln
x
⋅
y
=
ln
x
+
ln
y
\ln x·y=\ln x+\ln y
lnx⋅y=lnx+lny
ln
x
y
=
ln
x
−
ln
y
\ln \frac{x}{y}=\ln x-\ln y
lnyx=lnx−lny
ln
x
y
=
y
⋅
ln
x
\ln x^y=y·\ln x
lnxy=y⋅lnx
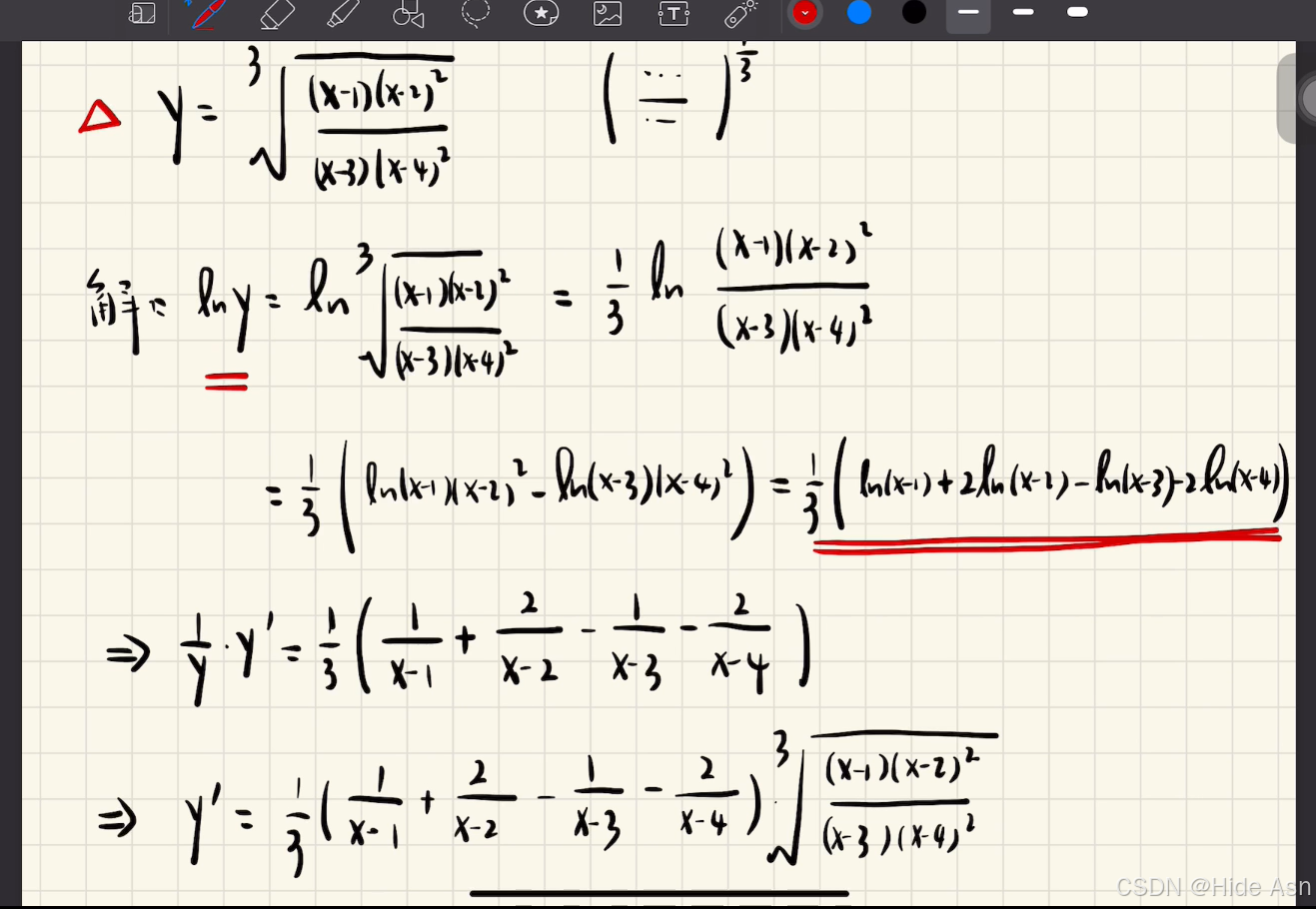
例：
例2：
扫一扫
933
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
