为什么需要特征值、特征向量和奇异值及其几何理解
为什么要研究特征值和特征向量
在实际应用中环境以及事物总是复杂的,由其产生的数据的高维的和直观上的无规律的,那么一般情况为了对高维的数据进行分析,从原始数据出发总是困难的,因此为了更好地理解事物或问题,我们倾向于将事物分解为更小的组件,并通过了解这些更小的组件来理解事物的属性。当我们把事物分解成最基本的组成部分或基本元素时,我们就能对事物有一个很好的理解。例如对于木桌,我们可以从木材材料和结构等基本要素的方面出发;因此,对高维的无直观规律的数据我们也希望能够通过一些分解变换的方法得到他的一些关键或者主要信息。而对于一个数据形成的矩阵来说,在原始的参考坐标下不明显的规律当更换参考系后会在特定方向产生明显的规律,而特征向量描述的是主要的一些规律变化的方向,即数据的主要特征。
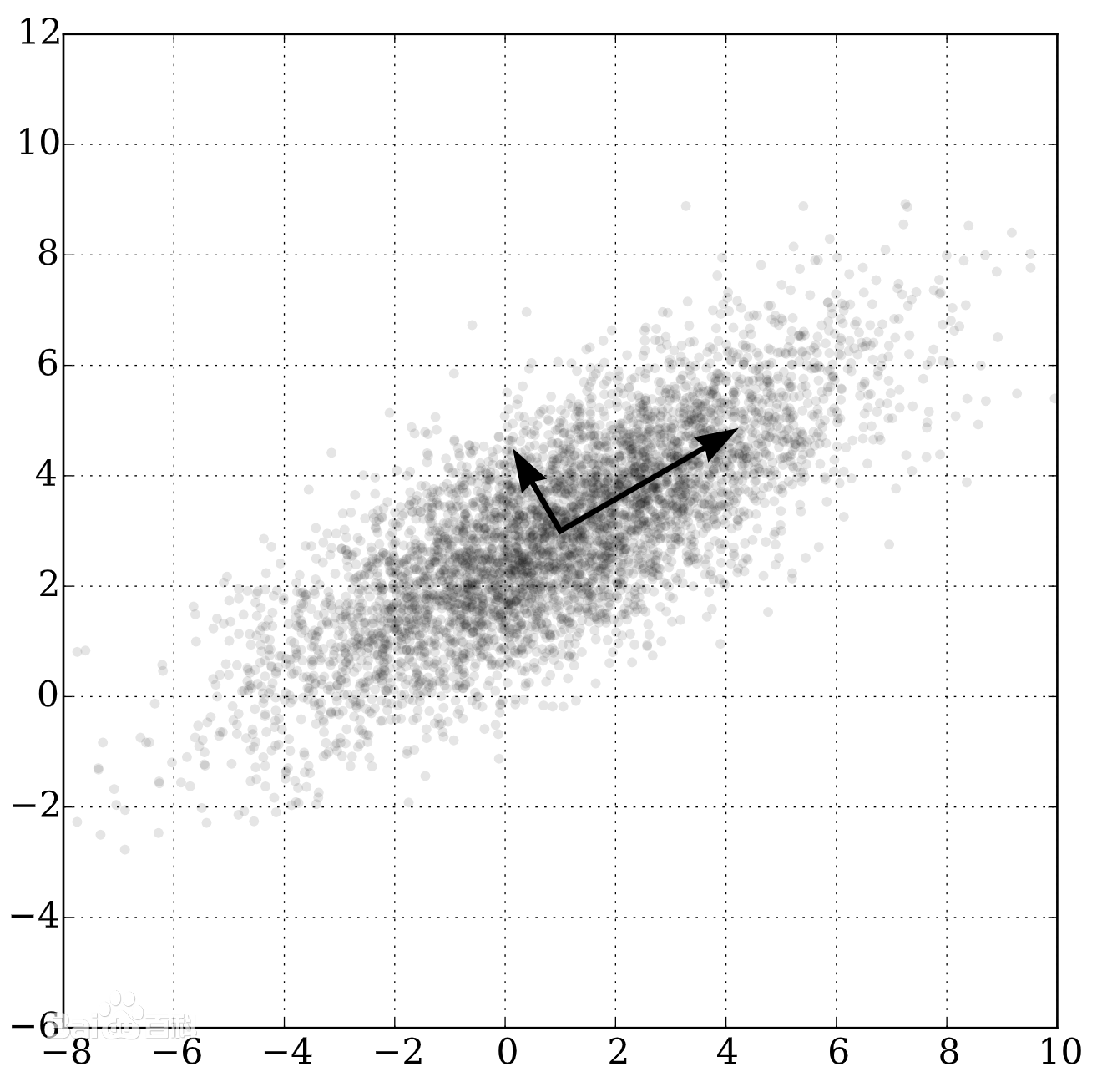
矩阵的意义
-
矩阵的几何意义:
一个m*n的矩阵可以理解为把一个向量从m维空间到n维空间的线性映射或者线性变换。- 对角矩阵:M与一个向量相乘的结果如下图,对角矩阵作用的几何意义为将向量在x的方向拉伸3倍,y方向拉伸一倍的线性变化。
[ 3 0 0 1 ] [ x y ] = [ 3 x y ] \left[ \begin{matrix} 3 & 0 \\ 0 & 1\\ \end{matrix} \right] \left[ \begin{matrix} x\\ y\\ \end{matrix} \right]= \left[ \begin{matrix} 3x\\ y\\ \end{matrix} \right] [3001][xy]=[3xy]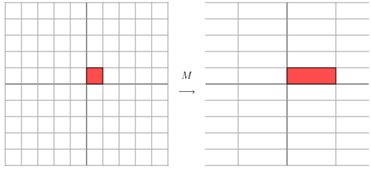
- 非对称矩阵:对于一个非对称矩阵,其几何意义为在平面上对一个轴进行拉伸变化(蓝色箭头)。
M = [ 1 1 0 1 ] M= \left[ \begin{matrix} 1 & 1 \\ 0 & 1\\ \end{matrix} \right] M=[1011]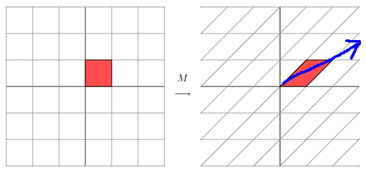
- 对角矩阵:M与一个向量相乘的结果如下图,对角矩阵作用的几何意义为将向量在x的方向拉伸3倍,y方向拉伸一倍的线性变化。
-
特征值和特征向量
- 对于给定的方阵M,一向量v经过矩阵的变换后,新向量v’与原来的v保持在同一直线上,仅仅做了长度上的缩放和方向上的不变或翻转,则对应的成为特征向量,长度变化幅值为特征值。
- 即特征向量描述的是在矩阵的线性变换过程中的不变量。
A x = λ x Ax=\lambda x Ax=λx
- 物理意义:矩阵所有的特征向量组成了这个向量空间的一组基底。而矩阵作为变换的本质其实就是把一个基底下的向量变换到另一个基底表示的空间中,因此特征向量代表的就是矩阵的本质特征。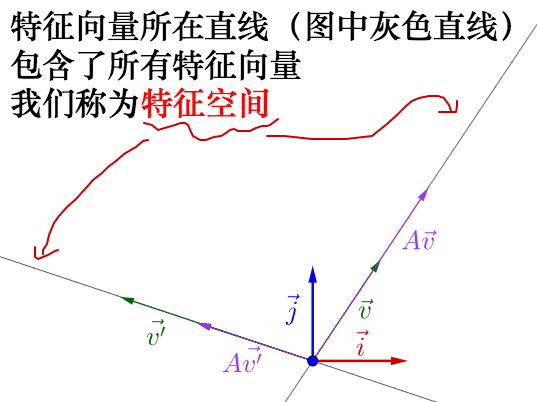
-
特征值分解(EVD)
- 对于对阵矩阵A,mxm维度,它有m个特征值和特征向量,将其展开后合并便可以得到
A x 1 = λ 1 x 1 A x 2 = λ 2 x 2 . . . A x m = λ m x m Ax_1=\lambda_1x_1\\ Ax_2=\lambda_2x_2\\ ...\\ Ax_m=\lambda_mx_m Ax1=λ1x1Ax2=λ2x2...Axm=λmxm
矩阵形式可以进一步化简,同时由于对称矩阵的特征向量两两正交,因此U是正交矩阵,其逆矩阵等于其转置
A U = U Λ A = U Λ U T U = [ x 1 x 2 ⋯ x m ] Λ = [ λ 1 . . . 0 ⋮ ⋱ ⋮ 0 . . . λ m ] AU=U \Lambda\\ A=U\Lambda U^T\\ U = [x_1 \: x_2 \: \cdots \: x_m]\\ \Lambda=\left[ \begin{matrix} \lambda_1 &...& 0 \\ \vdots & \ddots & \vdots \\ 0 &...& \lambda_m\\ \end{matrix} \right] AU=UΛA=UΛUTU=[x1x2⋯xm]Λ=⎣ ⎡λ1⋮0...⋱...0⋮λm⎦ ⎤因此特征值分解便将原来的矩阵变化A分解为U'的正交变换(旋转变换)、对变换后向量的拉伸或者压缩,最后在经过U的旋转变换的三个过程。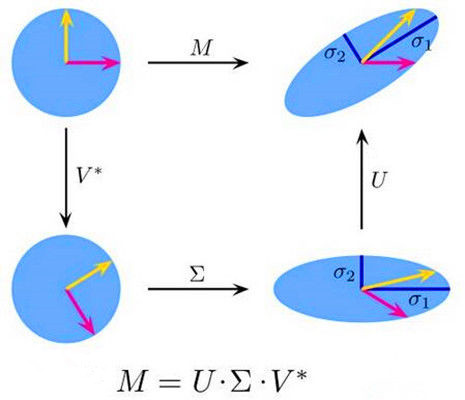
- 对于对阵矩阵A,mxm维度,它有m个特征值和特征向量,将其展开后合并便可以得到
奇异值和奇异分解(SVD)
-
奇异值分解(SVD)
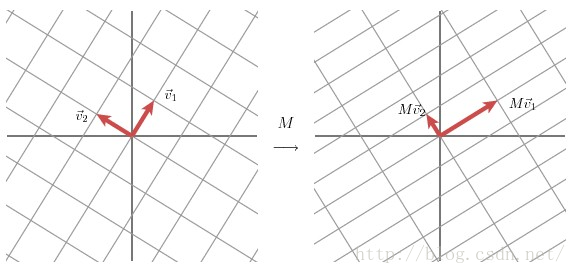
- 上述的特征值分解只能对方阵而言,但是实际应用中,大部分矩阵都不是矩阵,是mxn的非方阵,因此无法从方阵出发直接计算其特征值和不变量特征向量,因此退而求其次希望找到一组两两正交单位向量序列,其经过矩阵变换后变换后依然是是相互正交。
-
奇异值分解推导:对于一组正交单位向量 v 1 v_1 v1和 v 2 v_2 v2,变换后的 M v 1 Mv_1 Mv1和 M v 2 Mv_2 Mv2也是正交的,其中 u 1 u_1 u1和 u 2 u_2 u2是 M v 1 Mv_1 Mv1和 M v 2 Mv_2 Mv2的单位向量,即
M v 1 = σ 1 u 1 , M v 2 = σ 2 u 2 M = M [ v 1 v 2 ] [ v 1 T v 2 T ] = [ σ 1 u 1 σ 2 u 2 ] [ v 1 T v 2 T ] = [ u 1 u 2 ] [ σ 1 0 0 σ 2 ] [ v 1 T v 2 T ] M = U Σ V T Mv_1=\sigma_1u_1, \quad Mv_2=\sigma_2u_2\\ M=M\left[ \begin{matrix} v_1 & v_2 \end{matrix} \right] \left[ \begin{matrix} v_1^T \\ v_2^T \end{matrix} \right]= \left[ \begin{matrix} \sigma_1u_1 & \sigma_2u_2 \end{matrix} \right] \left[ \begin{matrix} v_1^T \\ v_2^T \end{matrix} \right]= \left[ \begin{matrix} u_1 & u_2 \end{matrix} \right] \left[ \begin{matrix} \sigma_1 & 0\\ 0 & \sigma_2 \end{matrix} \right] \left[ \begin{matrix} v_1^T \\ v_2^T \end{matrix} \right]\\ \qquad\\ M = U\Sigma V^T Mv1=σ1u1,Mv2=σ2u2M=M[v1v2][v1Tv2T]=[σ1u1σ2u2][v1Tv2T]=[u1u2][σ100σ2][v1Tv2T]M=UΣVT
V矩阵是一个原始空间的正交矩阵,它的每一个列向量都是原始空间的规范正交基;而U矩阵则是变换之后的域的正交矩阵,它的每一个列向量都是变换空间的规范正交基。而式子中的奇异值对角矩阵 Σ \Sigma Σ的值则对应了从原始空间(V)到变换空间(U)的对应关系,具体来说就是两个空间的基向量的拉伸程度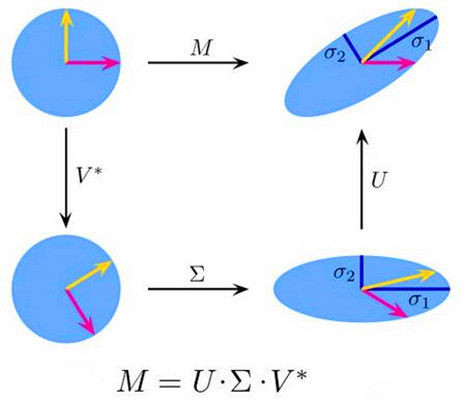
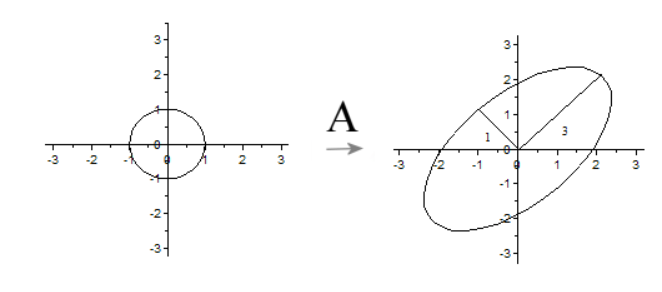

-
奇异值求解
在n维空间中找一组正交基,使得经过M变换后还是正交的。假设已经找到这样一组正交基 { v 1 v 2 . . . v n } \lbrace v_1 \: v_2 \: ... \: v_n \rbrace {v1v2...vn}经过A矩阵映射后 { M v 1 M v 2 . . . M v n } \lbrace Mv_1 \: Mv_2 \: ... \: Mv_n \rbrace {Mv1Mv2...Mvn},则要是他们两两正交
M v i . M v j = ( M v i ) T M v j = v i T M T M v j = 0 Mv_i.Mv_j=(Mv_i)^TMv_j=v_i^TM^TMv_j=0 Mvi.Mvj=(Mvi)TMvj=viTMTMvj=0
根据假设有 v j T v j = v i . v j = 0 v_j^Tv_j=v_i.v_j=0 vjTvj=vi.vj=0
如果v和 λ i \lambda_i λi为矩阵 M T M M^TM MTM的特征向量和特征值,因为 M T M M^TM MTM是对称矩阵,则v之间一定是两两针脚,则
v i T M T M v j = v i T λ j v j = λ j v i T v j = λ j v i . v j = 0 v_i^TM^TMv_j=v_i^T\lambda_jv_j=\lambda_jv_i^Tv_j=\lambda_jv_i.v_j=0 viTMTMvj=viTλjvj=λjviTvj=λjvi.vj=0
这样就找到了一组正交基在映射后依然是正交基,这一组正交基便是 M T M M^TM MTM的特征向量,之后对正交基进行单位化
M v i . M v i = v i T M T M v i = λ i v i . v i = λ i ∣ M v i ∣ 2 = λ i u i = M v i ∣ M v i ∣ = 1 λ i M v i M v i = σ i u i σ i = λ i Mv_i.Mv_i=v_i^TM^TMv_i=\lambda_i v_i.v_i=\lambda_i\\ \:\\ |Mv_i|^2=\lambda_i \\ \:\\ u_i=\frac{Mv_i}{|Mv_i|}=\frac{1}{\sqrt{\lambda_i}}Mv_i\\ \:\\ Mv_i=\sigma_iu_i \\ \quad \\ \sigma_i=\sqrt{\lambda_i} Mvi.Mvi=viTMTMvi=λivi.vi=λi∣Mvi∣2=λiui=∣Mvi∣Mvi=λi1MviMvi=σiuiσi=λi
则有
M = U Σ V T U = [ u 1 u 2 ⋯ u n ] Λ = [ σ 1 . . . 0 ⋮ ⋱ ⋮ 0 . . . σ n ] V = [ v 1 v 2 ⋯ v n ] M=U\Sigma V^T\\ \:\\ U = [u_1 \: u_2 \: \cdots \: u_n]\\ \:\\ \Lambda=\left[ \begin{matrix} \sigma_1 &...& 0 \\ \vdots & \ddots & \vdots \\ 0 &...& \sigma_n\\ \end{matrix} \right]\\ \:\\ V = [v_1 \: v_2 \: \cdots \: v_n] M=UΣVTU=[u1u2⋯un]Λ=⎣ ⎡σ1⋮0...⋱...0⋮σn⎦ ⎤V=[v1v2⋯vn] -
奇异值的意义
奇异值及其奇异向量给出了从m维空间的一组正交基的作用,通过矩阵映射变换到n维空间正交基中影响作用最大的一组方向和对应的幅值。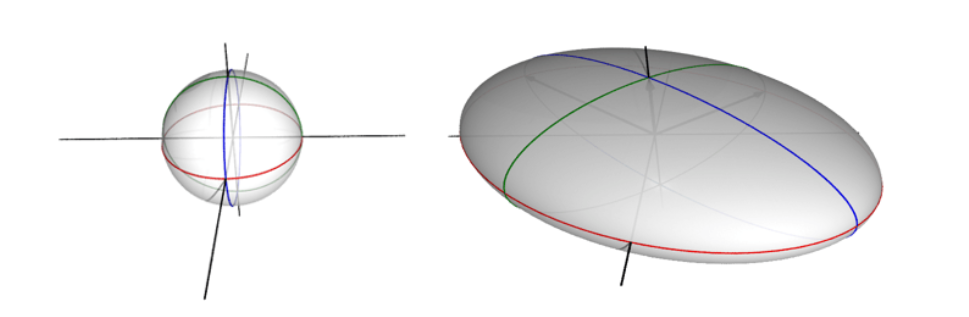
参考文章
[1] 奇异值分解(SVD)原理详解及推导: https://blog.csdn.net/zhongkejingwang/article/details/43053513
[2] 特征值分解、奇异值分解、PCA概念整理: https://blog.csdn.net/jinshengtao/article/details/18448355
[3] 【线性代数】通俗的理解奇异值以及与特征值的区别,还有奇异值分解及其应用: https://blog.csdn.net/qq_32742009/article/details/82286434
[4] Understanding Eigenvalues and Singular Values: https://mathformachines.com/posts/eigenvalues-and-singular-values/
[5] Understanding Singular Value Decomposition and its Application in Data Science: https://towardsdatascience.com/understanding-singular-value-decomposition-and-its-application-in-data-science-388a54be95d
[6] 奇异值的物理意义是什么?https://www.zhihu.com/question/22237507/answer/53804902























 7680
7680

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










