背景
离散控制过程系统,可用一个线性随机微分方程来描述:
系统状态:
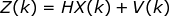
系统测量值:
X(k)是k时刻的系统状态;
U(k)是k时刻对系统的控制量;
A和B是系统参数,对于多模型系统,他们为矩阵;
Z(k)是k时刻的测量值,
H 是测量系统的参数,对于多测量系统,H 为矩阵。
W(k)、V(k)分别表示过程和测量的噪声。他们被假设成高斯白噪声(White Gaussian Noise),他们的 方差 分别是Q、R。
对于满足上面的条件(线性随机微分系统,过程和测量都是高斯白噪声),卡尔曼滤波器是最优的信息处理器。
卡尔曼五个基本公式
假设现在的系统状态是k,根据系统的模型,可以基于系统的上一状态而预测出现在状态:
预测值:
X(k|k-1):是利用上一状态预测的结果;
X(k-1|k-1):是上一状态最优的结果;
U(k):为现在状态的控制量,如果没有控制量,它可以为0;
对应于X(k|k-1)的协方差矩阵:
协方差:
P(k|k-1)是X(k|k-1)对应的协方差;
P(k-1|k-1)是X(k-1|k-1)对应的协方差;
Q是系统过程的协方差;
结合预测值和测量值,我们可以得到现在状态(k)的最优化估算值X(k|k):
最优估计值:
中Kg为卡尔曼增益(Kalman Gain);
卡尔曼增益:
R是测量噪声的协方差;
为了要另卡尔曼滤波器不断的运行下去直到系统过程结束,我们还要更新k状态下X(k|k)的协方差:
协方差更新:
其中I为对角元素为1的对角阵,对于单模型单测量,I=1。
当系统进入k+1状态时,P(k|k)就是式2的P(k-1|k-1)。
这样,算法就可以自回归的运算下去。
-
举例
这个姿态解算存在很多问题,不建议实际使用,只建议学习下思想
我们以陀螺仪、加速度计传感器为例,讲解如何实现卡尔曼滤波:
下面我们从卡尔曼滤波的五个基本公式,来一步步推导程序为何这样写:
Step 1 :基于系统的上一状态的预测值
陀螺仪有个静态漂移(而且还是变化的),静态漂移就是静止了没有角速度然后陀螺仪也会输出一个值,这个值肯定是没有意义的,计算时要把它减去:
rate = GyroRate - bias;减去零骗再经过积分,即可得陀螺仪计算出来的角度:
angle = angle + rate*dt;其中等号左边 angle 是当前计算出来的角度; 右边 angle 是上一次计算的角度;dt是两次滤波之间的时间间隔;
bias也是一个变化的量,但是就预测来说认为现在的漂移跟上一时刻是相同的即
bias = bias
将两个式子写成矩阵的形式:

我们令:

这样就得到了第一个基本公式: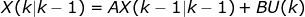 ;
;
Step 2 :对应于X(k|k-1)的协方差更新
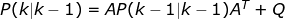
这里首先要给出两个值,一个是漂移的噪声,一个是角度值的噪声,(所谓噪声就是数据的方差值)
这里的Q为向量 的协方差矩阵,即:
的协方差矩阵,即: ;
;
因为漂移噪声还有角度噪声是相互独立的,则:
cov(bias,angle) = 0
cov(angle,bias) = 0
又因为 cov(x,x) = D(x)
所以上面的协方差矩阵可以简化为:
这里的两个方差值是开始就给出的常数,程序中的定义如下:Q_angle = 9.99999977E-3;Q_bias = 5.49999997E-2;
设: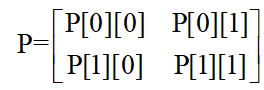 ,则:
,则:

于是就有如下程序:
P[0][0] += dt * (dt*P[1][1] - P[0][1] - P[1][0] + Q_angle);
P[0][1] -= dt * P[1][1];
P[1][0] -= dt * P[1][1];
P[1][1] += Q_bias * dt;Step 3 :计算卡尔曼增益
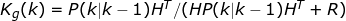
设: ,因为是直接测量的,所以设:
,因为是直接测量的,所以设:![]() ,则:
,则:

程序中先计算分子,然后分子 ÷ 分母:
S = P[0][0] + R_measure;
K[0] = P[0][0] / S;
K[1] = P[1][0] / S;Step 4:计算最优估计值
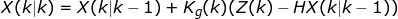
Z(k)是k时刻的角度测量值,这里既是加速度测量的角度 Acc_Angle;

程序中先计算角度误差,然后再乘增益k:
angle_err = Acc_Angle - angle; //角度误差
angle += K[0] * angle_err;
bias += K[1] * angle_err;Step 5:更新k状态下X(k|k)的协方差
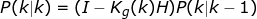
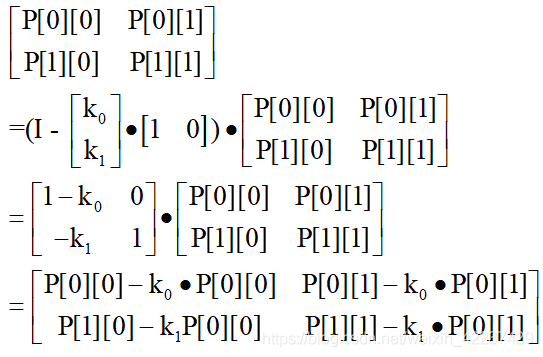
于是便有如下程序:
P[0][0] -= K[0] * P[0][0];
P[0][1] -= K[0] * P[0][1];
P[1][0] -= K[1] * P[0][0];
P[1][1] -= K[1] * P[0][1];程序如下:
float Q_angle;
float Q_bias;
float R_measure;
static float angle; //角度
static float bias; //陀螺仪漂移
static float rate; //角速度
static float P[2][2]; //误差协方差矩阵
void Kalman_Init(void)
{
Q_angle = 9.99999977E-3;//角度噪声协方差
Q_bias = 5.49999997E-2; //陀螺仪漂移噪声协方差
R_measure = 0.03f; //角度测量噪声
angle = 0.0f; //复位角度
bias = 0.0f; //复位陀螺仪漂移
P[0][0] = 0.0f; //协方差矩阵
P[0][1] = 0.0f;
P[1][0] = 0.0f;
P[1][1] = 0.0f;
}
//dt:周期
//Gyro:陀螺仪角速度值
//Accel:加速度计算出来的角度
void Kalman_getAngle(float dt,float Gyro_rate,float Acc_Angle)
{
float K[2]; //卡尔曼增益
float S; //计算卡尔曼增益时候的分母
float angle_err; //计算最优估计值时的角度误差
/* Step 1 */
//基于系统的上一状态的预测值
rate = Gyro_rate - bias;//陀螺仪:角速度 - 角速度漂移
angle = angle + rate*dt;//陀螺仪角速度积分成的角度=
/* Step 2 */
//对应于X(k|k-1)的协方差更新
P[0][0] += dt * (dt*P[1][1] - P[0][1] - P[1][0] + Q_angle);
P[0][1] -= dt * P[1][1];
P[1][0] -= dt * P[1][1];
P[1][1] += Q_bias * dt;
/* Step 3 */
//计算卡尔曼增益
S = P[0][0] + R_measure; //分母
K[0] = P[0][0] / S;
K[1] = P[1][0] / S;
/* Step 4 */
//计算最优估计值
angle_err = Acc_Angle - angle; //角度误差
angle += K[0] * angle_err;
bias += K[1] * angle_err;
/* Step 5 */
//更新k状态下X(k|k)的协方差
P[0][0] -= K[0] * P[0][0];
P[0][1] -= K[0] * P[0][1];
P[1][0] -= K[1] * P[0][0];
P[1][1] -= K[1] * P[0][1];
};







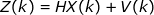
















 1197
1197

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








