求数的绝对值一定是正数_初中数学之绝对值，掌握绝对值的非负性，体会数形结合思想...

进入初中数学，更重要的是学会很多的数学思想，在以后的解题中能够熟练应用，更深刻的理解初中数学的精髓。对于刚进入初一的同学们来说，体会各种数学思想，尤为重要。今天我们一起来学习一下绝对值，绝对值这一节可以说非常的重要，在初中的学习中，时常会遇到，而绝对值与数轴的结合正好体现了数形结合的思想，在现在以及以后的学习中非常的重要，也是考试常考的题型。下面我们一起来学习一下本节的知识。

考点一：绝对值

首先明确绝对值的概念，一个数a的绝对值就是数轴上表示数a的点与原点的距离。记做|a|,这里需要注意的是，由于绝对值是两点间的距离，因此绝对值一定是大于等于0的，也就是说非负数。绝对值的判断法则：(1)一个正数的绝对值是它本身；(2)一个负数的绝对值是它的相反数；(3)0的绝对值是0。即对于任意有理数a,都有

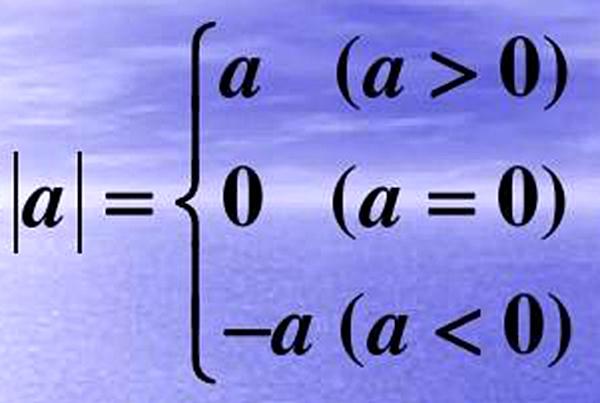
例题1：|π﹣3.14|=__________．

分析：首先确定π-3.14与0的大小关系，然后在去绝对值，π约为3.1415926，那么π-3.14>0，因此有判断法则可知，等于它本身π-3.14.这里尤其注意的是，在去绝对值是，是看绝对值内整体与0的大小关系，而不是只看其中的部分，整体大于0，那么等于它本身，整体小于0，那么等于它的相反数，也就是在前面加一个“-”即可。

考点二：绝对值的性质

对于概念需要注意的几点：1、任何数都有绝对值，且只有一个，无论a取何有理数，都有lal≥0，即任何一个有理数的绝对值都是非负数，若几个非负数的和为0，那么这几个非负数均为0。绝对值最小的数是0。2、由绝对值的判断法则可知：当lal=a时，a取正数和0；当lal=-a时，a取负数和0。3、互为相反数的两个数的绝对值相等；绝对值相等的两个数相等或互为相反数.4、在数轴上，一个数离原点越近，则它的绝对值越小；离原点越远，则它的绝对值越大。5、绝对值是某个正数的数有两个，他们互为相反数。

例题2：已知|x-2|与|y+5|互为相反数，求x-y的值

分析：根据相反数的定义，可知|x-2|+|y+5|=0，根据绝对值的非负性可知，|x-2|=0，|y+5|=0，然后根据绝对值的定义，可知x-2=0，y+5=0，求得x=2,y=-5.所以可以求出x-y=2-(-5)=7.

这里常考的就是绝对值的非负性，以及化简绝对值。绝对值的化简是本节的重点，也是难点，而且是整个初中阶段理解起来比较困难的知识点之一，必须深刻理解绝对值的含义。做到以后做题得心应手。

考点三：有理数的比较大小

方法1、利用数轴进行有理数大小的比较。在数轴上，从左往右就是从小到大的顺序，即数轴上左边的数小于右边的数。方法二、根据前面学的正数、0、负数，可知正数大于0,0大于负数，正数大于负数，对于两个负数的大小比较，绝对值大的反而小。

例题3：如图，a、b是有理数，则下列结论正确的是( )

A．-b＜-a＜a＜b； B．-a＜-b＜a＜b；

C．-b＜a＜-a＜b； D．-b＜b＜-a＜a。

分析：本题考察的数形结合思想，可以根据绝对值以及相反数的相关知识，在数轴上画出-a,-b的位置，根据有理数的大小比较，结合数轴，从左往右，逐渐变大，因此本题选C.

关于绝对值，其实还有很多重点和难点，后面将会一一介绍，本节大家还要学会分类讨论的思想，因为在去绝对值的时候，会出现两个结果，因此必须分类讨论。如果有问题可以留言，后面将会一一介绍。