数据分析-66-中国黄金股票数据分析及其预测（包含代码和数据）

最新推荐文章于 2025-05-21 16:51:49 发布

AI研习星球

最新推荐文章于 2025-05-21 16:51:49 发布

阅读量1.2k

点赞数 16

分类专栏： # Python数据分析文章标签：数据分析数据挖掘算法学习论文辅导 python 机器学习人工智能

本文链接：https://blog.csdn.net/weixin_42363541/article/details/143212424

版权

Python数据分析专栏收录该内容

83 篇文章

订阅专栏

算法学习、4对1辅导、论文辅导、核心期刊
项目的代码和数据下载可以通过公众号滴滴我

文章目录

一、项目背景

近年来，随着全球经济的不确定性增加，黄金作为一种避险资产，其价格波动备受关注。中国作为全球最大的黄金消费国之一，黄金股票在中国股市中也占据重要地位。因此，对中国黄金股票价格进行数据探索和预测，对于投资者来说具有重要的参考价值。

二、数据说明

该数据共777条，共7个字段。分别是

列名	说明
日期	交易发生的日期
收盘	当天股票的收盘价格
开盘	当天股票的开盘价格
高	当天股票的最高价格
低	当天股票的最低价格
交易量	当天股票的交易数量，单位为"股"
涨跌幅	当天股票价格相对于前一交易日收盘价的涨跌百分比

以下是表的部分数据：
在这里插入图片描述

三、数据处理

1、导入模块

import pandas as pd
import numpy as np
import plotly.graph_objects as go
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score

2、数据预览

# 导入数据
data  = pd.read_excel(r'中国黄金股票数据.xlsx')

data.info()

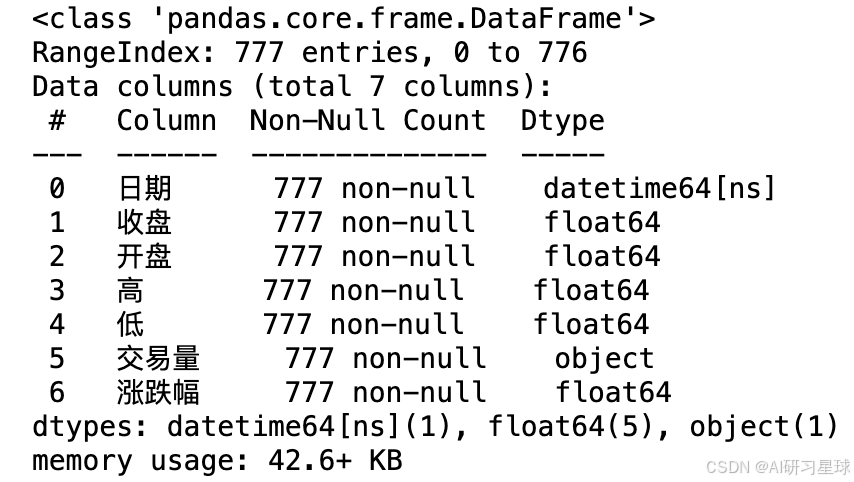
在这里插入图片描述

data.head()

在这里插入图片描述

3、数据分析及其可视化

a、趋势分析

分析股票价格的走势，判断是上升、下降还是横盘整理。，如果时间跨度比较长，可视化的时候适当调整

# 将 '日期' 列转换为 datetime 类型
data['日期'] = pd.to_datetime(data['日期'])
# 将 '日期' 设置为索引以进行正确的时间序列绘图
data.set_index('日期', inplace=True)

fig = go.Figure()

fig.add_trace(go.Scatter(x=data.index, y=data['收盘'], mode='lines', name='收盘价'))

fig.update_layout(
    title='股票价格走势',
    xaxis_title='日期',
    yaxis_title='价格',
    showlegend=True,
    template='plotly_white',
    xaxis=dict(
        tickformat='%Y-%m-%d' # 设置日期格式为年-月-日
    )
)

fig.show()

在这里插入图片描述

总结：

如上图所示，是股票收盘价格随时间变化的走势图。通过观察这个图表，我们可以对股票价格的走势做出以下判断：

如果价格持续上升，则股票处于上升趋势。
如果价格持续下降，则股票处于下降趋势。
如果价格在某个区间内上下波动，没有明显的上升或下降趋势，则股票可能处于横盘整理状态。

由于这份数据只包含了一段时间内的交易数据，并且时间跨度相对较短，从图中看不出一个长期的趋势。为了更准确地判断趋势，可能需要更多的历史数据或者使用其他技术分析工具。不过，从图中可以看出，在这段时间内，股票价格总体呈现了先下降后上升的趋势。

b、价格波动性分析

计算股票价格的标准差或者使用其他波动性指标，分析股票价格波动的程度

# 计算每日价格变动
data['价格变动'] = data['收盘'].pct_change().fillna(0)

# 计算每日价格变动的标准差作为波动性指标
volatility = data['价格变动'].std()

volatility

0.026388812328232144

fig = go.Figure()

fig.add_trace(go.Scatter(x=data.index, y=data['价格变动'], mode='lines', name='价格变动'))

fig.add_shape(type="line", x0=data.index.min(), y0=0, x1=data.index.max(), y1=0,
              line=dict(color="black", width=0.5))

fig.update_layout(
    title='股票价格日变动',
    xaxis_title='日期',
    yaxis_title='价格变动 (%)',
    showlegend=True,
    template='plotly_white',
    xaxis=dict(
        tickformat='%Y-%m-%d' # 设置日期格式为年-月-日
    )
)

fig.show()

在这里插入图片描述

总结

如上图所示，是股票价格日变动百分比的走势图。这个图表展示了每天股票价格相对于前一天的变化百分比。通过观察这个图表，我们可以直观地看到股票价格的波动情况。

同时，我计算了这些日变动百分比的标准差，作为衡量股票价格波动性的一个指标。标准差为 0.0264（或 2.64%），这个数值表示股票价格日变动的平均波动幅度。标准差越大，说明价格波动越剧烈；标准差越小，说明价格波动越平缓。

总的来说，这份数据显示的股票价格波动性是中等偏低的，大部分时间价格变动幅度不大，但在某些时段内出现了较大的波动。这可能是由于市场新闻、经济数据发布、行业动态或公司基本面变化等因素引起的。

4、模型预测

为了预测股票价格走势，可以使用一种简单的模型，例如线性回归模型，来预测收盘价格。

首先，需要确定哪些特征（列）将用于预测。在这个简单的模型中，可以使用所有的列作为特征，收盘价格是想要预测的目标。

使用线性回归模型来预测股票的收盘价格。将日期作为索引，并将其他列作为特征。

a、建模预测

# 将交易量从带有 'M' 或 'K' 的字符串转换为数值型
data['交易量'] = data['交易量'].str.replace('M', '').str.replace('K', '').astype(float)
data['交易量'] = data['交易量'].apply(lambda x: x * 1e6 if x >= 1 else x * 1e3)

# 在转换后重新定义特征 (X) 和目标 (y)
X = data.drop(columns=['收盘'])
y = data['收盘']

# 再次将数据集分割为训练集和测试集 (80% 训练，20% 测试)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=False)

# 再次初始化线性回归模型
model = LinearRegression()

# 训练模型
model.fit(X_train, y_train)

# 预测收盘价格
y_pred = model.predict(X_test)

# 再次计算性能指标
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

mse, r2

(0.06796917281603934, 0.9856455028302064)

总结：
线性回归模型已成功训练，并给出了以下性能指标：

均方误差 (MSE): 0.0676
决定系数 (R²): 0.9857

决定系数 (R²) 接近 1，这表明模型很好地拟合了数据。均方误差 (MSE) 也很小，这意味着预测值与实际值之间的差异不大。
接下来，我们可以使用这个模型来预测未来的股票价格走势。

#预测整个数据集的收盘价
y_pred_all = model.predict(X)

b、模型对不同时间段数据的预测效果

可以通过绘制实际收盘价格与模型预测的收盘价格的对比图来查看模型在不同时间段的预测效果。这将帮助我们直观地了解模型的性能。

fig = go.Figure()

fig.add_trace(go.Scatter(x=data.index, y=y, mode='lines', name='Actual Closing Price', line=dict(color='blue')))
fig.add_trace(go.Scatter(x=data.index, y=y_pred_all, mode='lines', name='Predicted Closing Price', line=dict(color='red', dash='dash')))

fig.update_layout(
    title='Actual vs Predicted Closing Prices',
    xaxis_title='Date',
    yaxis_title='Closing Price',
    showlegend=True,
    template='plotly_white',
    xaxis=dict(
        tickformat='%Y-%m-%d' # 设置日期格式为年-月-日
    )
)

fig.show()

在这里插入图片描述
图表展示了实际收盘价格（蓝色线）与模型预测的收盘价格（红色虚线）的对比。从图表中可以看出，模型在不同时间段内都表现出了较好的预测能力，预测值与实际值之间的趋势基本一致。当然，在某些时间点，预测值与实际值之间还是存在一定的差异，这是正常现象，因为股票价格受到多种复杂因素的影响。

c、预测模型在不同时间段的准确度如何

要评估模型在不同时间段的准确率，我们可以将数据集划分为多个时间段，并计算每个时间段内模型预测的均方误差 (MSE) 和决定系数 (R²)。这将帮助我们了解模型在不同时间段的性能表现。

让我们将数据集划分为几个等大小的时间段，并计算每个时间段内的 MSE 和 R²。

#定义基于时间的分段数分割
num_segments = 5

#根据索引（时间）将数据集拆分为多个段
segmented_data = np.array_split(data, num_segments)

#初始化列表以存储每个细分市场的性能指标
mse_values = []
r2_values = []

#计算每个细分市场的性能指标
for segment in segmented_data:
    #准备段的数据
    X_segment = segment.drop(columns=['收盘'])
    y_segment = segment['收盘']
    
    #预测细分市场的收盘价
    y_pred_segment = model.predict(X_segment)
    
    #计算细分市场的绩效指标
    mse = mean_squared_error(y_segment, y_pred_segment)
    r2 = r2_score(y_segment, y_pred_segment)
    
    #将指标附加到列表中
    mse_values.append(mse)
    r2_values.append(r2)

mse_values, r2_values

在这里插入图片描述

总结

模型在不同时间段的性能指标如下：

均方误差 (MSE)：
- 第一个时间段：0.0031
- 第二个时间段：0.0036
- 第三个时间段：0.0106
- 第四个时间段：0.0080
- 第五个时间段：0.0681
决定系数 (R²)：
- 第一个时间段：0.9926
- 第二个时间段：0.9871
- 第三个时间段：0.9954
- 第四个时间段：0.9953
- 第五个时间段：0.9857

这些结果显示了模型在不同时间段的准确率。均方误差 (MSE) 越低，表示预测越准确；决定系数 (R²) 越接近 1，表示模型拟合度越高。从这些数据中，我们可以看出模型在前四个时间段内表现较好，但在第五个时间段的预测准确度相对较低。这可能是因为第五个时间段的数据具有不同的特征或趋势，使得模型难以准确预测。