文章目录
栈
单调栈
单调栈有单调递增栈和单调递减栈,单调栈的原理就是保证栈内元素是有序的,当加入一个栈中的元素破坏这个属性的时候就pop出栈中元素。单调栈的变体就是栈内存着的是元素的索引,通过索引判断栈内元素是否有序。
单调栈用来解决温度递增 柱状图面积等问题
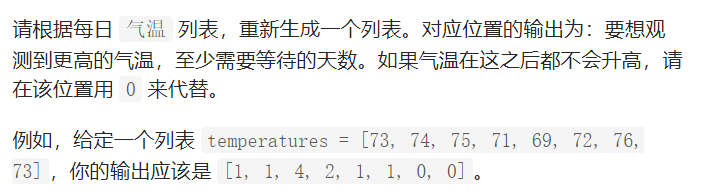
class Solution {
public:
vector<int> dailyTemperatures(vector<int>& temperatures) {
vector<int> res(temperatures.size(),0);
stack<int> record;
for(int i = 0; i < temperatures.size();i++)
{
if(record.empty())
{
record.push(i);
continue;
}
else
{
if(temperatures[i] <= temperatures[record.top()])
{
record.push(i);
continue;
}
else
{
while((!record.empty()) && (temperatures[record.top()] < temperatures[i]))
{
int temp = record.top();
record.pop();
res[temp] = i - temp;
}
record.push(i);
}
}
}
return res;
}
};

class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int> boundStack;
vector<int> leftBound(heights.size(),0);
vector<int> rightBound(heights.size(),0);
//确定左边界
for(int i = 0; i < heights.size();i++)
{
while(!boundStack.empty() && (heights[boundStack.top()] >= heights[i]))
{
boundStack.pop();
}
if(boundStack.empty())
{
leftBound[i] = -1;
}
else
{
leftBound[i] = boundStack.top();
}
boundStack.push(i);
}
boundStack= stack<int>(); //把栈中内存清空
//确定右边界
for(int i = heights.size()-1;i >= 0;i--)
{
while(!boundStack.empty() && (heights[boundStack.top()] >= heights[i]))
{
boundStack.pop();
}
if(boundStack.empty())
{
rightBound[i] = heights.size();
}
else
{
rightBound[i] = boundStack.top();
}
boundStack.push(i);
}
int maxSize = 0;
for(int i = 0;i < heights.size();i++)
{
int curSize = (rightBound[i] - leftBound[i]-1) * heights[i];
if(curSize > maxSize)
{
maxSize = curSize;
}
}
return maxSize;
}
};
树
树的深度遍历和广度遍历
广度遍历可以用队列,深度遍历可以递归或者用栈来实现非递归。
树的前序遍历和中序遍历以及后序遍历的非递归实现
struct tree
{
int value;
tree* leftChild;
tree* rightChild;
};
tree* getTree()
{
tree* res = new tree{ 1,nullptr };
tree* res1 = new tree{ 2,nullptr };
tree* res2 = new tree{ 3,nullptr };
tree* res3 = new tree{ 4,nullptr };
tree* res4 = new tree{ 5,nullptr };
tree* res5 = new tree{ 16,nullptr };
res->leftChild = res1;
res->rightChild = res2;
res1->leftChild = res3;
res1->rightChild = res4;
res2->leftChild = res5;
return res;
}
void forwardTravese() //前序遍历
{
tree* head = getTree();
stack<tree*> stkTree;
stkTree.push(head);
while (!stkTree.empty())
{
tree* cur = stkTree.top();
stkTree.pop();
cout << cur->value << " " << endl; //这一行就是打印当前遍历点
if (cur->rightChild != nullptr)
{
stkTree.push(cur->rightChild);
}
if (cur->leftChild != nullptr)
{
stkTree.push(cur->leftChild);
}
}
}
void midTraverse() //中序遍历,中序遍历比较复杂,首先是只考虑父节点的一个右节点,然后等遍历到了这个右节点,又以这个右节点为根节点继续
{
tree* p = getTree();
stack<tree*> stkTree;
while (p != nullptr)
{
while (p != nullptr)
{
if (p->rightChild != nullptr)
{
stkTree.push(p->rightChild);
}
stkTree.push(p);
p = p->leftChild;
}
//先打印一下最左边的左节点
p = stkTree.top();
stkTree.pop();
while ((p->rightChild == nullptr) && (!stkTree.empty())) //这一块的代码很灵性
{
cout << p->value << " " << endl; //单边树
p = stkTree.top();
stkTree.pop();
}
cout << p->value << " " << endl; //如果有右子树,把父节点打印出来
if (!stkTree.empty())
{
p = stkTree.top(); //像一个新子树一样中序遍历
stkTree.pop();
}
else
{
p = nullptr;
}
}
}
二叉树的查找 插入 删除
二叉树的删除除了分三种情况考虑如何移动元素,对于空间的删除也要搞清楚,删除的是移动的指针空间内容,这个个空间内容已经被分配给了之前指向删除空间的指针。
tree* searchTree(int value, tree* &root)//查找
{
if (root == nullptr)
{
return nullptr;
}
tree* res = root;
while (res != nullptr)
{
if (res->value == value)
{
return res;
}
else if (res->value > value)
{
res = res->leftChild;
}
else
{
res = res->rightChild;
}
if (res == nullptr)
{
return nullptr;
}
}
return res;
}
void insertTree(int value, tree* &root)//插入
{
if (root == nullptr)
{
root = new tree{ value,nullptr,nullptr };
return;
}
tree* s = root;
while (s != nullptr)
{
tree* old = s;
if (s->value == value)
{
return;
}
else if (s->value > value)
{
s = s->leftChild;
if (s == nullptr)
{
old->leftChild = new tree{ value,nullptr,nullptr };
}
}
else
{
s = s->rightChild;
if (s == nullptr)
{
old->rightChild = new tree{ value,nullptr,nullptr };
}
}
}
}
void deleteTree(int value, tree* &root) //删除
{
tree* dTree = nullptr;
dTree = searchTree(value, root);
if (dTree == nullptr)
{
return;
}
//分三种情况处理
//dTree没有右子树
if (dTree->rightChild == nullptr)
{
tree* temp = dTree->leftChild;//这是关键***********
(*dTree) = (*dTree->leftChild); //不用删除空间,只需要对内存位置重新赋值就可以了******
delete temp; //删除被移动的空间*********
return;
}
//dTree没有左子树
if (dTree->leftChild == nullptr)
{
tree* temp = dTree->rightChild;
(*dTree) = (*dTree->rightChild);
delete temp;
return;
}
//dTree左子树和右子树都存在,把当前节点的右子树嫁接到左子树的最右
tree* temp = dTree->leftChild;
while (temp->rightChild != nullptr)
{
temp = temp->rightChild;
}
temp->rightChild = dTree->rightChild;
temp = dTree->leftChild;
(*dTree) = (*dTree->leftChild);
delete temp;;
return;
}
int main()
{
tree* root = nullptr;
insertTree(9, root);
insertTree(6, root);
insertTree(15, root);
insertTree(5, root);
insertTree(7, root);
insertTree(11, root);
insertTree(3, root);
insertTree(8, root);
forwardTravese(root);
tree* target = searchTree(7,root);
if (target != nullptr)
{
cout << &(*target) << " :" << target->value << endl;
}
else
{
cout << "no the value " << endl;
}
deleteTree(6, root);
forwardTravese(root);
}
AVL树和红黑树
AVL树和红黑树的设计目标都是为了保持树的平衡的,就是防止树退化成链表,影响算法性能。然后具体都设计了插入和删除的规则。
B树和B+树
B树是主要用于设计这个磁盘和内存中数据交互用的,因为B树一个节点可以存储很多键值,节点大小较大,这样可以节约磁盘IO次数和时间。B树一个节点最多可以有m个键值和m-1个子节点,B树必须是半满的这个由插入和删除的规则来保证。B+树在B树的基础上,B树每个节点都保存了数据,但是B+树只有叶子几点才保存数据,这样便于遍历整个树。
图
图的数据存储方式
二维矩阵存储,邻接矩阵,适用于密度较高,比较小的图。
链表存储,邻接表,适用于密度较低,比较大的图,对于一写比如拓扑排序等也很适合。
图的深度优先搜索
#include<iostream>
#include<array>
#include<vector>
#include<algorithm>
#include<string>
#include<deque>
using namespace::std;
const int arraySize = 6;
const int self = 0;
const int unreach = 1000;
int graph[arraySize][arraySize] = {
{self,7,3,unreach,unreach,unreach},
{unreach,self,unreach,unreach,5,unreach},
{unreach,unreach,self,2,2,unreach},
{unreach,unreach,unreach,self,unreach,6},
{unreach,unreach,unreach,unreach,self,3},
{unreach,unreach,unreach,unreach,unreach,self}
};
vector<int> visited = { 0,0,0,0,0,0 };
//DFS 深度优先搜索 找到起点到终点的所有路径
void DFSsearchPath(int start, int target,vector<int>& path,vector<vector<int>> &res)
{
if (visited[start] == 1) //已经走过
return;
else
{
path.push_back(start);//加入路径
visited[start] = 1;//记录已经走过
}
for (int j = 0; j < arraySize; j++)
{
if ((graph[start][j] != self) &&( graph[start][j] != unreach))//0表示此路可以走
{
if (j == target) //到达终点
{
path.push_back(j);
res.push_back(path);
path.pop_back();
visited[target] = 0;
continue;
}
DFSsearchPath(j, target, path, res); //递归调用
visited[path.back()] = 0; //记录是否走过, 回退就是没有走
path.pop_back();//回退
}
}
}
图的广度优先搜索
void BFSSearchPath(int start, int target, deque<int>& p,vector<int> &path, vector<vector<int>>& res) //广度优先搜索算法不适合找到所有路径,但是可以找到一条最短路径
{
p.push_back(start);
path.resize(6, 0);
int distance[6] = { 0,1000,1000,1000,1000,1000 };//记录路径成本
while (p.size() != 0)
{
int currentPlace = p.front();
p.pop_front();
for (int i = 0; i < arraySize; i++)
{
if ((graph[currentPlace][i] != self) && (graph[currentPlace][i] != unreach))//0表示此路可以走
{
int dis = distance[currentPlace] + graph[currentPlace][i];
if ((i != target) && (dis < distance[i])) //这里相当于一个剪枝操作
{
distance[i] = dis;
path[i] = currentPlace;
p.push_back(i);
}
else if((i == target) && (dis < distance[target]))
{
distance[target] = dis;
path[i] = currentPlace;
}
}
}
}
cout << distance[target] << endl;
cout << target;
while (path[target] != 0)
{
cout << path[target];
target = path[target];
}
cout << path[target] << endl;
}
图最小生成树
kruskal算法
对于一个图,将其中存在的所有边按照从大到小排序,然后依次取出最小的边,并将边中的顶点加入到最小生成树中,但是不允许形成闭环,也就是加入一个边的时候需要判断边中的两个顶点是否都已经在生成树中了,生成树的记录需要一个顶点集合和一个边集合。
prim算法
首先从图中任意选择一个顶点,找到与此顶点中相连的最小边,将边上的另一个顶点加入到最小生成树,继续判断与这个最小生成树中所有顶点相连的最小边将其加入到最小生成树中,(不能形成闭环,也就是边的另一个顶点不能在最小生成树中),直到所有顶点都被加入到最小生成树中。
vector<int> getMinTreePrim()
{
vector<int> res;
res.resize(6, 0);
int alreadInVertex[6] = { 1,0,0,0,0,0 };
int countAddVertex = 1;
while (true)
{
//在已经存在的生成树的列表里找到一个最近的顶点
int minDistance = unreach;
int vertex = 0;
int father = 0;
for (int i =0; i < arraySize;i++)
{
if (alreadInVertex[i] != 1)
{
continue;
}
for (int j = 1; j < arraySize; j++)
{
if (((graph[i][j] < minDistance) && (alreadInVertex[j] != 1))) //判断j不能已经在生成树中
{
minDistance = graph[i][j];
vertex = j;
father = i;
}
}
}
res[vertex] = father;//加入最小生成树
alreadInVertex[vertex] = 1; //加入最小生成树,做好边标记
countAddVertex++;
if (countAddVertex == arraySize) //打印出来
{
for (int i = 0; i < arraySize; i++)
{
cout << i <<" : " <<res[i] << endl;
}
break;
}
}
return res;
}
图拓扑排序
拓扑排序主要是用在工期活动图中,工程任务之间有先后关系,工程任务必须在其先导任务都完成后,才能开工。
这个问题适用于邻接表的数据结构,对每一个顶点记录它的入度和出度,都这个工程完成时,把以其作为先导的任务的入度减一,当一个工程的入度等于0之后,就可以将其加入拓扑队列中(表示可以开工了),拓扑队列不唯一。
关键路径算法
首先初始化每个顶点的最早开始为0,然后对AOE网进行拓扑排序,在排序的过程中获取每个顶点的最早开始时间;
获取拓扑排序后,初始化每个顶点的最晚开始时间为汇点的最早开始时间,并从AOE网的汇点开始,从后往前,对每个顶点找到求其最晚开始时间;
遍历图中的每条边(方法是遍历图中每个顶点的边表),求其最早开始时间和最晚开始时间,如果二者相等,则这是个关键活动,将其加入关键路径中。
dijkstra 单源最短路径
主要是计算图中各顶点到起始点的最短路径。首先创建一个大小位顶点数目的数组dis,记录各顶点到起始点的距离,不能直达的顶点记为大数。然后维护一个数组book记录哪些顶点已经被计算过最短路径,初始只有顶点自己在这个数组中。然后对于所有未计算最短距离的顶点e,找出距离起点最近的顶点,在dis中,然后将这个顶点加入到record中,同时判断dis中各顶点中与顶点e相连的顶点经过e点到达起点的距离是否更近,如果是更新dsi数组中的值(松弛更新)。直到所有顶点都被计算一边。

void dijisktra() //记录所有顶点到最后一个顶点的距离
{
int distance[6] = { graph[0][5],graph[1][5],graph[2][5],graph[3][5],graph[4][5],graph[5][5] };
int record[6] = { 0,0,0,0,0,1 };// 记录是否被计算过最短距离
int countNum = 1; // 记录加入过的顶点数目
while (true)
{
int minDistance = unreach;
int addNum = 0;
for (int i = 0; i < arraySize; i++) //寻找一个最近的顶点
{
if ((record[i] == 0) && (distance[i] < minDistance))
{
addNum = i;
minDistance = distance[i];
}
}
//将最近的顶点加入到已处理顶点记录中,并且对其他顶点松弛(就是看经过这个顶点是否更快到达目标)
record[addNum] = 1;
countNum++;
for (int i = 0; i < arraySize; i++)
{
if ((distance[addNum] + graph[i][addNum]) < distance[i]) //对顶点距离松弛判断
{
distance[i] = (distance[addNum] + graph[i][addNum]);
}
}
if (countNum == arraySize)
{
for (int i = 0; i < arraySize; i++)
{
cout << i << " : " << distance[i] << endl;
}
break;
}
}
}
Bellman-Ford 解决负权边算法
dijkstra算法不能解决负权边的问题,dijkstra是基于贪心策略,每次都找一个距源点最近的点,然后将该距离定为这个点到源点的最短路径;但如果存在负权边,那就有可能先通过并不是距源点最近的一个次优点,再通过这个负权边,使得路径之和更小,这样就出现了错误。
BFD算法的思想是从边入手,每次考虑以某个边作为中转路径,是否能够缩短两点的距离,最多经过(n-1)调边中转。
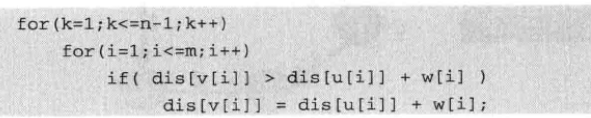
Floyd 多源最短路径算法
Folyd算法的核心就是对于任意两点之间的距离,选择一个中间顶点过度,看是否能够缩短距离。实际代码执行是按照,选择一个顶点作为中间点,更新所有能够通过此中间点而缩短距离的顶点间距离。画个图试验一下就知道算法的正确定。算法的复杂度未o(N3),三层循环。

最大流
网络图中从源点到目标点的最大流量。这个问题可以转化为最小割最大流,就是将网络图中所有顶点分为两个集合一个集合包含起点,一个包含源点,然后计算这两个集合间的最大流。所有割中最小的最大流就是网络中的最大流。
实际计算最大流的方法有增广路径法,就是找出从起点到目标点的路径,并且计算这个路径的最大流,然后将所有路径中的所有边减去这个最大流,同时增加一个反向流。路径的寻找可以用DFS或者BFS算法,直到找不到路径为止。边的容量为0表示边不通。
字符串算法
BF 暴力匹配算法
就是最简单的暴力匹配,算法复杂度O(mn),是大部分标准库的算法,因为一般字符串比较小,这个算法简单可靠。
RK 哈希匹配
计算字符串的哈希值进行匹配,对于哈希值的计算要有合理利用主串中的重复字符的哈希值。哈希算法的复杂度O(n);
BM算法
BM算法的核心就是倒着匹配字符串,当遇到不匹配的字符是,就直接移动字串直到子串中的字符与当前主串中字符匹配。

#include<string>
#include<iostream>
using namespace::std;
int BM(string s, string p)
{
int pos = p.size() - 1;
int sSize = s.size() - 1;
int pSize = p.size() - 1;
int cursor = 0;
int bias = 0; //pos指针需要的偏移量
while ((cursor <= pSize) && (pos <= sSize))
{
if (p[pSize - cursor] == s[pos - cursor])
{
cursor++;
continue;
}
else
{
while ((pSize - cursor - bias) >= 0 &&(p[pSize - cursor -bias] != s[pos - cursor]))//坏字符
{
bias++;
}
pos = pos + bias; //主串偏移
bias = 0;
cursor = 0;
}
}
if (cursor == (pSize+1))
{
return (pos - pSize );
}
return -1;
}
int main()
{
string s = "gg good boyoyagh g";
string p = "boyoya";
cout << BM(s, p) << endl;
}
kmp算法
kmp算法的核心是next数组,每次遇到不匹配的字符的时候就去next数组找到当前主串中的字符应该匹配模式串中的位置。

next[B] = C 也就是说 next[5] = 2;
所以构建next函数是KMP算法的最核心。
vector<int> getNext(string sp)
{
vector<int> resNext;
resNext.resize(sp.size());
resNext[0] = -1;
int j = 0; //遍历给next数组赋值
int k = -1;
while (j < (sp.size()-1))
{
if ((k == -1) || sp[j] == sp[k])
{
j++;
k++;
resNext[j] = k; //如果是重复子串,这里面包含的意思就是sp[0] ...sp[k-1] == sp[t-k]...sp[t-1];
}
else
{
k = resNext[k];//如果不重复,就去next[k]中记录的还是重复子串,直到k == -1;
}
}
return std::move(resNext);
}
int KMP(string t, string p)
{
int posT = 0;
int posP = 0;
vector<int> next = getNext(p);
int pSize = p.size();
int tSize = t.size();
while ((posP < pSize) && (posT < tSize))
{
if (p[posP] == t[posT])
{
posP++;
posT++;
continue;
}
else if(posP >= 0)
{
posP = next[posP];
}
if(posP == -1)
{
posP = 0;
posT++;
continue;
}
}
if (posP == p.size() )
{
return (posT - p.size()+1);
}
return -1;
}
trie树 (字典树)


#include<string>
#include<iostream>
#include <vector>
using namespace::std;
struct trieTree
{
char value;
trieTree* child;
trieTree* next;
};
class trie
{
public:
trieTree* tree = nullptr;
public:
trie() {};
~trie()
{
deleteTrie(tree);
};
public:
void insert(string s)
{
int start = 0;
if (s.size() == 0)
{
return;
}
trieTree* t = this->tree;
trieTree* tail = this->tree;
trieTree* fathert = t;
if (this->tree == nullptr)//第一次初始化
{
this->tree = new trieTree{ s[0],nullptr,nullptr };
trieTree* temp = this->tree;
for (int j = 1; j < s.size(); j++)
{
temp->child = new trieTree{ s[j],nullptr,nullptr };
temp = temp->child;
}
return ;
}
int sSize = s.size();
for (int i = 0; i < sSize; i++)
{
if (findCharInTheLevel(s[i], t, tail) != nullptr)
{
fathert = t;
t = fathert->child;
continue;
}
else
{
tail->next = new trieTree{ s[i],nullptr,nullptr };
trieTree* newTree = tail->next;
for (int j = i + 1; j < sSize; j++) //后面的字符存储都需要新的节点
{
newTree->child = new trieTree{ s[j],nullptr,nullptr };
newTree = newTree->child;
}
return;
}
if (t == nullptr)
{
for (int j = i + 1; j < sSize; j++)
{
fathert->child = new trieTree{ s[j],nullptr,nullptr };//后面的字符存储都需要新的节点
fathert = fathert;
}
return;
}
}
}
bool findSameString(string s)
{
trieTree* node = this->tree;
for (auto ch : s)
{
trieTree* temp = node;
node = findCharInTheLevel(ch, node, temp);
if (node == nullptr)
{
return false;
}
else
{
node = node->child;
}
}
if(node == nullptr)
return true;
return false;
}
private:
void deleteTrie(trieTree* tree)
{
if (tree != nullptr)
{
deleteTrie(tree->next);
deleteTrie(tree->child);
delete tree;
}
};
trieTree* findCharInTheLevel(char ch, trieTree* tree,trieTree* &tail )
{
trieTree* res = nullptr;
tail = tree;
while (tree != nullptr)
{
if (tree->value == ch)
{
res = tree;
return res;
}
tail = tree;
tree = tree->next;
}
return res;
}
};
int main()
{
trie tr;
tr.insert("iost");
tr.insert("immt");
tr.insert("momot");
cout << tr.findSameString("imm") << endl;
}
排序算法

插入排序和希尔排序
插入排序就是一个一个将后面的元素插入到目标位置,这个算法要大量移动元素,算法效率极低。希尔排序是在插入排序的改进,插入排序可以理解为间隔1个元素,而希尔元素一开始选择间隔较大的序列,让这一组序列有序,逐渐缩小间隔,直到间隔为1。
//希尔排序
//希尔排序的本质是通过构建子序列 利用插入排序,让子序列有序,然后逐渐缩小子序列的数目
//希尔排序的优点在于能够将靠后的较小数据尽快移动到前面,在较少的移动次数情况下
void shellSort(vector<int>& vecInt)
{
int gap = vecInt.size() / 2;
while (gap > 0)
{
for (int i = 0; i<gap; i++)
{
for (int j = i; j < vecInt.size(); j += gap)
{
int index = j;
while (true)
{
if (index < gap) break;
else if (XLessY(vecInt[index], vecInt[index - gap]))
{
int temp = vecInt[index];
vecInt[index] = vecInt[index - gap];
vecInt[index - gap] = temp;
index-= gap;
}
else
{
break;
}
}
}
}
gap /= 2;//增量减小
}
}
冒泡排序和归并排序
冒泡排序就是调整两个相连元素的位置,对整个数组遍历两遍。
归并排序是数组不断一分为2,对两个子数组继续一分为2,直到只有两个元素的时候,对其排序,然后有序合并子数组。归并排序空间复杂度为o(n);个人觉得归并算法的性能最好。
//归并排序,是冒泡排序的改进,先将整个列表不断划分到2个元素的子列表,然后对子列表排序合并
void mergeSort(vector<int>& nums, int i, int j)
{
if (j <= i)
{
return;
}
if ((j - i) == 1)
{
if (XLessY(nums[j], nums[i]))
{
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
return;
}
}
else
{
//归并排序
mergeSort(nums, i, (i + j) / 2);
mergeSort(nums, (i + j) / 2 + 1,j);
merge(nums, i, (i + j) / 2, (i + j) / 2 + 1, j);
}
}
void merge(vector<int>& nums, int i, int j, int m, int k)
{
//用临时空间排序
int start = i;
vector<int> temp;
while ((i <= j) || (m <= k))
{
if ((i <= j) & ( ((m > k) ||(XLessY(nums[i],nums[m]))) ))
{
temp.push_back(nums[i]);
i++;
}
else if (m <= k)
{
temp.push_back(nums[m]);
m++;
}
}
//归并
for (auto num : temp)
{
nums[start] = num;
start++;
}
}
选择排序和快速排序
选择排序是每次从未排序数据中选择一个最小的到排序的队尾。快速排序是利用一个轴,将数据分为小于轴的和大与轴的。这个算法的技巧在于如何将数据正确的移动到轴的左右两侧,可以先获取轴的值,然后将轴移动到最后的位置,然后从头遍历轴,将小于轴的元素交换到轴的前面,然后再与轴做一次交换。
//快速排序;应该算是选择排序的改进,每次选择一个基准,然后将小于基准的数据分到数字前面,
//大于基准的分到后面,递归
void quickSort(vector<int>& nums,int i,int j)
{
if (j <= i)
{
return;
}
//将轴移动到一端
int kivot = (i + j) / 2;
int temp = nums[kivot];
nums[kivot] = nums[j];
nums[j] = temp;
kivot = j;
for (int m = i; m < kivot; m++)
{
if (XLessY(nums[kivot] ,nums[m]))
{
//将m和轴前面一个元素交换
int temp = nums[kivot - 1];
nums[kivot - 1] = nums[m];
nums[m] = temp;
//将m和轴交换
int temp2 = nums[kivot - 1];
nums[kivot - 1] = nums[kivot];
nums[kivot] = temp2;
//重新调整游标
kivot--;
m--;
}
}
quickSort(nums, i, kivot - 1);
quickSort(nums, kivot+1,j);
}
堆排序
利用到完全二叉树的特点,子节点是父节点的2i+ 1 和 2 i+2;堆排序需要分为两个步骤,第一个步骤构建一个大顶堆,第二个步骤将大顶堆的第一个元素(最大元素)放到堆中最后位置,堆大小减一,并且重新对堆排序。
//堆排序
void adjustHeap(vector<int>& nums, int i, int j)
{
for (int k = 2 * i + 1; k < j; k = 2 * k + 1)//一撸到底的检查
{
if ((k + 1) < j)
{
if (XLessY(nums[k], nums[k + 1]))
{
k++;
}
}
if (XLessY(nums[i], nums[k])) //交换父子节点
{
int temp2 = nums[i];
nums[i] = nums[k];
nums[k] = temp2;
i = k;
}
else
{
break;
}
}
}
void heapSort(vector<int>& nums)
{
//对堆排序构建一个有序堆
//从第一个非叶子结点从下至上,从右至左调整结构
for (int i = (nums.size())/2 - 1; i >= 0; i--)
{
adjustHeap(nums, i, nums.size());
}
//2.调整堆结构+交换堆顶元素与末尾元素
for (int j = nums.size() - 1; j > 0; j--)
{
int temp = nums[0];
nums[0] = nums[j];
nums[j] = temp;
adjustHeap(nums, 0, j);
}
}






















 653
653











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








