同指数幂相减公式_指数对数幂函数，基础有问题就看这篇！

一、指数函数

要点1：指数函数的概念

要点诠释：

（1）形式上的严格性：

（2）为什么规定底数a大于零且不等于1：

要点2：指数函数的图象及性质

要点诠释：

要点3：指数函数底数变化与图像分布规律

（1）

（2）特殊函数

要点4：指数式大小比较方法

(1)单调性法：化为同底数指数式，利用指数函数的单调性进行比较.

(2)中间量法

(3)分类讨论法

(4)比较法

比较法有作差比较与作商比较两种，其原理分别为：

二、指数运算

要点1：整数指数幂的概念及运算性质

1．整数指数幂的概念

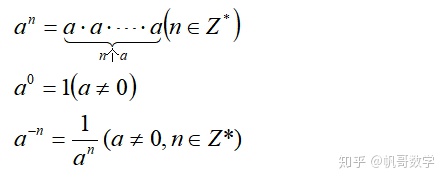
2．运算法则

要点2：根式的概念和运算法则

1．n次方根的定义：

2．两个等式

要点诠释：

①要注意上述等式在形式上的联系与区别；

要点3：分数指数幂的概念和运算法则

要点4：有理数指数幂的运算

1．有理数指数幂的运算性质

要点诠释：

(1)根式问题常利用指数幂的意义与运算性质，将根式转化为分数指数幂运算；

(2)根式运算中常出现乘方与开方并存，要注意两者的顺序何时可以交换、何时不能交换.

(3)幂指数不能随便约分.

2.指数幂的一般运算步骤

有括号先算括号里的；无括号先做指数运算．负指数幂化为正指数幂的倒数．

底数是负数，先确定符号，底数是小数，先要化成分数，底数是带分数，先要化成假分数，然后要尽可能用幂的形式表示，便于用指数运算性质．

在化简运算中，也要注意公式：a2－b2＝（a－b）（a＋b），（a±b）2＝a2±2ab＋b2，（a±b）3＝a3±3a2b＋3ab2±b3，a3－b3＝（a－b）（a2＋ab＋b2），a3＋b3＝（a＋b）（a2－ab＋b2）的运用，能够简化运算.

三、对数运算

要点1：对数概念

1.对数的概念

要点诠释：

3．两种特殊的对数

4．对数式与指数式的关系

由定义可知:对数就是指数变换而来的，因此对数式与指数式联系密切，且可以互相转化.它们的关系可由下图表示.

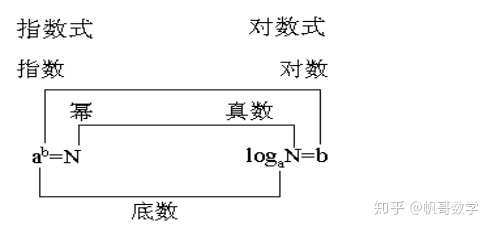
由此可见a，b，N三个字母在不同的式子中名称可能发生变化.

要点二、对数的运算法则

(1) 正因数的积的对数等于同一底数各个因数的对数的和；

​

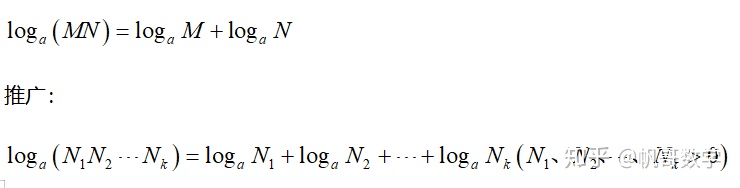
(2) 两个正数的商的对数等于被乘数的对数减去除数的对数；

(3) 正数的幂的对数等于幂的底数的对数乘以幂指数；

要点诠释：

（1）利用对数的运算法则时，要注意各个字母的取值范围，即等式左右两边的对数都存在时等式才能成立.

如：log2(-3)(-5)=log2(-3)+log2(-5)是不成立的，因为虽然log2(-3)(-5)是存在的，但log2(-3)与log2(-5)是不存在的.

（2）不能将和、差、积、商、幂的对数与对数的和、差、积、商、幂混淆起来

要点3：对数公式

1．对数恒等式：

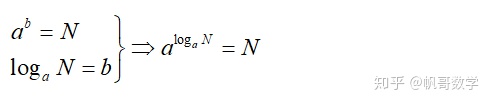
2．换底公式

同底对数才能运算，底数不同时可考虑进行换底，

当然，细心一些的同学会发现(1)可由(2)推出，但在解决某些问题(1)又有它的灵活性：

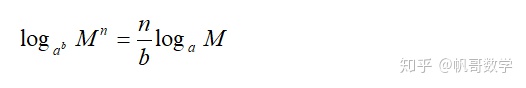
而且由(2)还可以得到一个重要的结论:

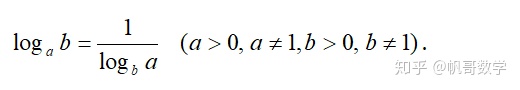
四、对数函数

要点1：对数函数的概念

要点诠释：

（2）求对数函数的定义域时应注意：①对数函数的真数要求大于零，底数大于零且不等于1；②对含有字母的式子要注意分类讨论．

要点2：对数函数的图象与性质

要点诠释：

下面介绍一种简单记忆方法，供同学们学习时参考.

要点3：底数对对数函数图象的影响

1．底数制约着图象的升降．

如图

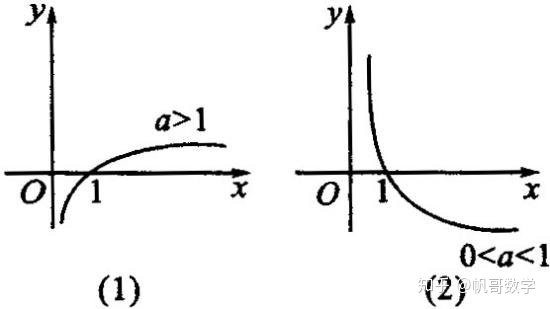
要点诠释：

由于底数的取值范围制约着对数函数图象的升降（即函数的单调性），因此在解与对数函数单调性有关的问题时，必须考虑底数是大于1还是小于1，不要忽略．

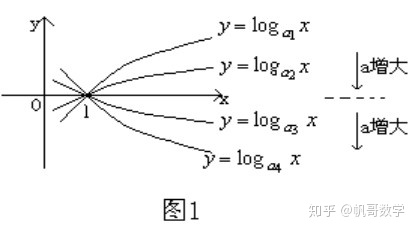
2．底数变化与图象变化的规律

五、幂函数

要点1：幂函数概念

要点诠释：

要点2：幂函数的图象及性质

1.作出下列函数的图象：

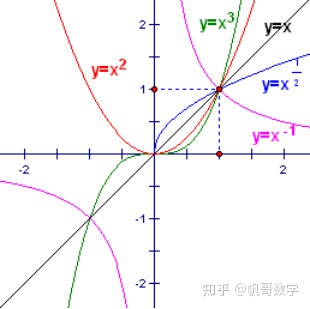
要点诠释：

2.作幂函数图象的步骤如下:

(1)先作出第一象限内的图象；

(2)若幂函数的定义域为(0，+∞)或[0，+∞)，作图已完成；

若在(-∞，0)或(-∞，0]上也有意义，则应先判断函数的奇偶性；

如果为偶函数，则根据y轴对称作出第二象限的图象；

如果为奇函数，则根据原点对称作出第三象限的图象.

3.幂函数解析式的确定

(1)借助幂函数的定义，设幂函数或确定函数中相应量的值．

(2)结合幂函数的性质，分析幂函数中指数的特征．

4.幂函数值大小的比较

(1)比较函数值的大小问题一般是利用函数的单调性，当不便于利用单调性时，可与0和1进行比较．常称为“搭桥”法．

(2)比较幂函数值的大小，一般先构造幂函数并明确其单调性，然后由单调性判断值的大小．

(3)常用的步骤是：①构造幂函数；②比较底的大小；③由单调性确定函数值的大小．