Frank-Wolfe法方法
1. 适用求解问题
Frank和Wolfe于1956年提出求解非线性规划带有线性约束问题的一种算法。
研究非线性问题:
m i n f ( x ) s . t . A x = b , x ≥ 0 \begin{aligned} min \quad &f(x) \\ s.t. \quad &Ax=b, \\ &x\ge0 \end{aligned} mins.t.f(x)Ax=b,x≥0
其中A是 m × n m \times n m×n , 秩为 m m m, b b b是 m m m纬列向量, f ( x ) f(x) f(x)是连续可微函数。
Frank-wolfe算法的基本思想是:在每次迭代过程中,将目标函数 f ( x ) f(x) f(x)线性化,通过解线性规划求得下降可行方向,进而沿此方向在可行域内作一维搜索。
2. 求解步骤
求解步骤参考陈宝林老师的《最优化理论与算法》一书,具体步骤如下:

3. 求解示例
测试问题:
m i n f ( x ) = x 1 2 + x 2 2 − x 1 × x 2 − 2 × x 1 + 3 × x 2 s . t . x 1 + x 2 + x 3 = 3 ; x 1 + 5 x 2 + x 4 = 6 ; x 1 , x 2 , x 3 , x 4 ≥ 0 \begin{aligned} min \quad &f(x)=x_1^2+x_2^2-x_1 \times x_2 -2\times x_1 + 3 \times x_2 \\ s.t. \quad &x_1+x_2+x_3=3; \\ & x_1 + 5x_2 + x_4=6; \\ & x_1,x_2,x_3,x_4 \ge0 \end{aligned} mins.t.f(x)=x12+x22−x1×x2−2×x1+3×x2x1+x2+x3=3;x1+5x2+x4=6;x1,x2,x3,x4≥0
设定初始解
x
=
(
2
,
0
,
1
,
4
)
T
x={(2,0,1,4)}^{T}
x=(2,0,1,4)T,迭代过程图如下:
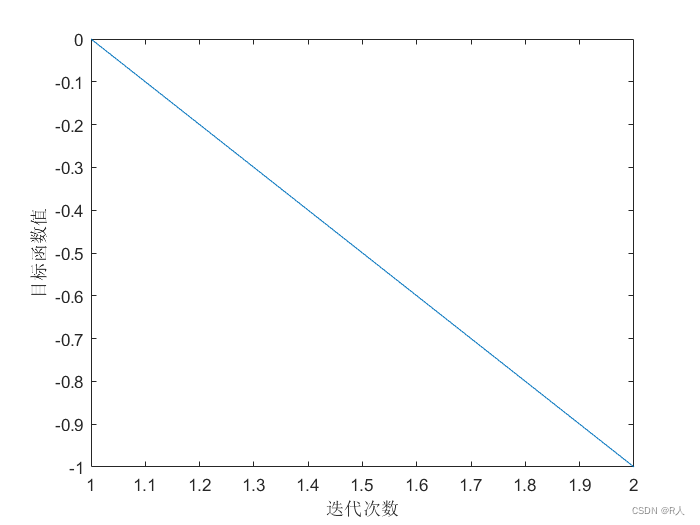
经过两次迭代找到最优解(K-T点)为 ( 1 , 0 , 2 , 5 ) T {(1,0,2,5)}^{T} (1,0,2,5)T,由于计算误差的存在,更改初始解往往fw方法往往不容易收敛,例如将初始解更改为 x = ( 0.5 , 1 , 0.5 , 0.5 ) T x={(0.5,1,0.5,0.5)}^{T} x=(0.5,1,0.5,0.5)T,迭代过程图如下:
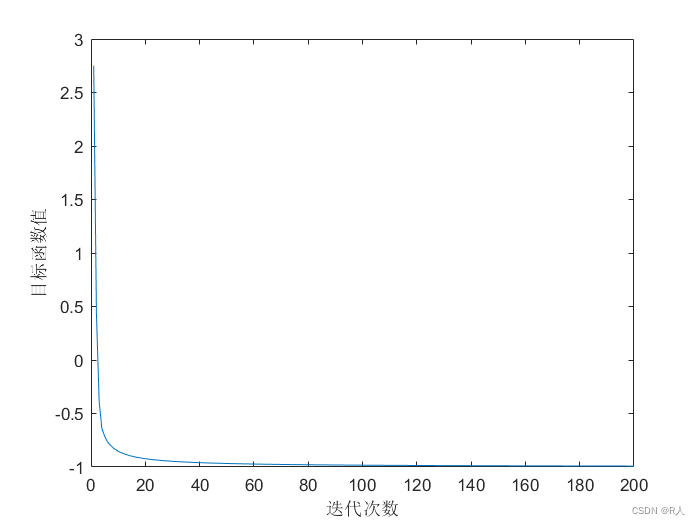
下面要介绍的梯度投影法没有这个问题。
梯度投影法
1. 适用求解问题
考虑问题
m i n f ( x ) s . t . A x ≥ b , E x = e \begin{aligned} min \quad &f(x) \\ s.t. \quad &Ax \ge b, \\ &Ex=e \end{aligned} mins.t.f(x)Ax≥b,Ex=e
其中 f ( x ) f(x) f(x)是可微函数, A A A为 m × n m\times n m×n矩阵, E E E为 l × n l\times n l×n矩阵;
梯度投影法的基本思想:从可行点出发,沿可行方向搜索,当迭代出发点再可行域内部时,沿负梯度方向搜索,当迭代出发点再某些约束的边界上时,将该点处的负梯度投影到 M M M的零空间, M M M是起约束或作用约束的梯度为行构造成的矩阵。同样,梯度投影也可以找到K-T点。
2. 求解步骤

3. 求解示例
测试问题:
m i n f ( x ) = 2 × x 1 2 + 2 × x 2 2 − 2 × x 1 × x 2 − 4 × x 1 − 6 × x 2 s . t . − x 1 − x 2 ≥ − 2 ; − x 1 − 5 x 2 ≥ − 5 ; x 1 , x 2 ≥ 0 \begin{aligned} min \quad &f(x)=2\times x_1^2 + 2\times x_2^2 - 2 \times x_1 \times x_2 - 4\times x_1 - 6 \times x_2 \\ s.t. \quad &-x_1-x_2 \ge -2; \\ & -x_1 - 5x_2 \ge -5; \\ & x_1,x_2 \ge0 \end{aligned} mins.t.f(x)=2×x12+2×x22−2×x1×x2−4×x1−6×x2−x1−x2≥−2;−x1−5x2≥−5;x1,x2≥0
设定初始解
x
=
(
0
,
0
)
T
x={(0,0)}^{T}
x=(0,0)T,找到最优解为
(
1.129
,
0.77419
)
T
{(1.129,0.77419)}^{T}
(1.129,0.77419)T。迭代过程图如下:
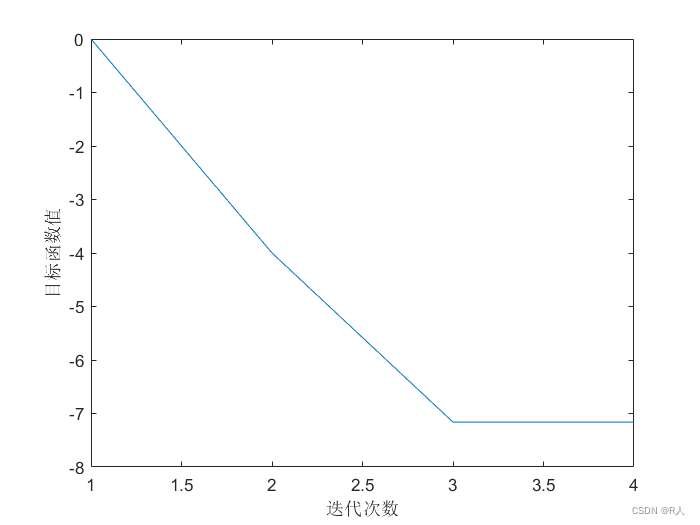





















 1707
1707











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








