高数笔记02：导数、微分、中值定理

梅头脑_

已于 2023-07-28 12:39:03 修改

阅读量1.4k

点赞数 2

分类专栏： # 高等数学文章标签：考研笔记学习

于 2023-07-26 21:20:14 首次发布

本文链接：https://blog.csdn.net/weixin_42789937/article/details/131946146

版权

高等数学专栏收录该内容

6 篇文章

订阅专栏

本文是作者学习高等数学第二、三章关于导数、微分和中值定理的笔记，包括概念理解、选填题目解析、计算题目示例以及相关定理的证明。文章详细探讨了导数的计算、连续性与可导性的关系，微分中值定理的基本介绍及其在证明和应用中的作用。同时，作者分享了复习资源和在线工具，供其他考研者参考。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

图源：文心一言

本文是我学习高等数学第二、三章导数、微分、中值定理的一些笔记和心得，希望可以与考研路上的小伙伴一起努力上岸~~🥝🥝

第1版：查资料、画导图、归纳题型~🧩🧩

参考资料1：《高等数学》同济大学数学系编

参考资料2：《高等数学基础篇》武忠祥

真题截图：2023考研数学复习辅导历年考研数学真题文都考研网 (wendu.com)

审核：BING AI

📇目录

🦮思维导图

思维导图为整理同济教材、武老师基础教材所列导数、微分、中值定理的内容，整理有点累哦，有兴趣复习概念的同学可以简单浏览一下~

🍃导数

🍂选填题目

🍂选填题目类型1：导数与微分的概念，分段函数或初等函数是否存在极限

计算法：求左导数与右导数，注意求闭区间端点导数可以使用求导公式，但求开区间端点导数即领域点导数时，需要使用左、右导数定义公式。
以增量 $\Delta x$ 与定点 $x_0$ 计算的公式： $\lim_{\Delta x \to 0+} \frac{\Delta y}{\Delta x}=\lim_{\Delta x \to 0+} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$

以函数值 $x$ 与定点 $x_0$ 计算的公式： $\lim_{\Delta x \to 0+} \frac{\Delta y}{\Delta x}=\lim_{\Delta x \to 0+} \frac{f(x)-f(x_0)}{x-x_0}$

例题【2021年数一 1题】

🍂选填题目类型2：连续、可导、可微的关系

一元函数，可导与可微能够互推，证明简述如下：
因为： $f'(x)+\alpha=\lim_{\Delta x \to 0} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$
所以： $f(x+x_0)-f(x_0)=f'(x_0)\Delta x+ o (\Delta x)$
注意：公式中的 $\alpha$ 与 $o (\Delta x)$ 都是无穷小量，表示近似~
一元函数，连续是可导、可微的前提条件；注意，导数存在不一定是可导，例如可去间断点的左极限等于右极限，只能说该点导数存在，不能说可导哦~
导数存在的前提条件：该点左、右导数存在且相等；
可导的前提条件：该点导数存在且连续；
连续不可推可导，同理不可推可微，举栗： $y=|x|$ 在 $x_0=0$ 。

图源YY的上上签：【高等数学】函数连续、可导、可微_YY的上上签

例题【2020年数一 2题】

答谢：感谢评论区I Like Doraemon的指正，这道题目确实是选C不是B哈！！😶‍🌫️😶‍🌫️

A、B肯定是不能选的，因为它犯了导数存在就是可导的错误，需要增加连续作为前提；
C是考试的正确答案，这个等式是导数的高阶无穷小，可以选；
D这个答案有歧义，在武老师的书上分母是 $x^2$ 而不是 $\sqrt{x^2}$ ，很多网上真题的题目分母是 $\sqrt{x^2}$ ，解答也是按照 $x^2$ 作为分母去验证的。那我们讨论两种情况：
假设题目分母是 $x^2$ 时，极限变形 $\lim_{x \to 0}\frac{f(x)-f(0)}{x-0}\cdot \frac{1}{x}$ ，可导表示前面的分式结果存在，后面的分式是无穷，所以没办法保证是无穷，例如f(x)=x时，整个分式就无穷了~
假设题目分母是 $\sqrt{x^2}$ 时，个人觉得也不能选， $\lim_{x \to 0}\frac{f(x)-f(0)}{x-0}\cdot \frac{x}{\sqrt{x^2}}$ ，可导表示前面的分式结果存在，且 $\sqrt{x^2}$ 与 $x$ 是等价无穷小，且正负号会带来变化，例如：
$f(x)=e^x-1$ ，经过0点，导数值存在；
$h(x)=\frac{e^x-1}{x}$ ，用等价无穷小化简，e^x-1~x，结果为1
$g(x)=\frac{e^x-1}{\sqrt{x}^2}$ ，在h(x)的基础上，因正负号不同，结果为+1和-1；
$p(x)=\frac{e^x-1}{\sqrt{|x|}}$ ，因为 $x$ 比 $\sqrt{x}$ 是高阶无穷小，所以结果为0；
我们上图表示：

当然，如果我再次说错了欢迎小伙伴在评论区批评留言，博主真的超级感谢！！🙏🙏

🍂计算题目

🍂 计算题目类型1，显函数求导数：

基本初等函数的导数公式

$C'=0$ ；
$(x^\alpha)'=\alpha x^{\alpha-1}$ ；
$(a^x)'=a^xlna$ ，特别地 $(e^x)'=e^x$ ；
$(log_ax)'=\frac{1}{xlna}$ ，特别地 $(ln|x|)'=\frac{1}{x}$ ；
$(sin(x))'=cos(x)$ ， $(cos(x))'=-sin(x)$ ；
$(tan(x))'=sec^2(x)$ ， $(cot(x))'=-csc^2(x)$ ；
$(sec(x))'=sec(x)tan(x)$ ， $(csc(x))'=-csc(x)cot(x)$ ；
$(arcsin(x))'=\frac{1}{\sqrt{1-x^2}}$ ， $(arccos(x))'=-\frac{1}{\sqrt{1-x^2}}$ ；
$(arctan(x))'=\frac{1}{1+x^2}$ ， $(arccot(x))'=-\frac{1}{1+x^2}$ ；

有理运算法则

$[u(x)±v(x)]'=u'(x)±v'(x)$ ；
$[u(x)v(x)]'=u'(x)v(x)+u(x)v'(x)$ ；
$[u(x)/v(x)]'=\frac{u'(x)v(x)-u(x)v'(x)}{v^2(x)}$ ， $v(x)\neq 0$

高阶导数有理运算法则

$[u(x)±v(x)]^{(n)}=u^{(n)}(x)±v^{(n)}$ ；
$(uv)^{(n)}=\sum_{k=0}^n C_n^ku^{(u-k)}v^{(k)}$ ； //展开公式对应二项式定理

😶‍🌫️😶‍🌫️以下是公式证明简介，个人整理便于记忆公式~

基本初等函数的导数公式证明简述

推导公式是这个： $\lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x}=\lim_{\Delta x \to 0} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$ ，注意 $\Delta x$ 是无穷小；话说忘记无穷小公式的同学可以看向本系列第一篇博文~

🌸高数笔记01：函数、极限、连续_梅头脑_的博客-CSDN博客

$C'=0$ ；
$f(x_0+\Delta x)-f(x_0)=C-C=0$ ；
$(x^\alpha)'=\alpha x^{\alpha-1}$ ；
$\alpha$ 为正整数n时，

代入公式，二项式展开

$\lim_{\Delta x \to 0} \frac{(x+\Delta x)^n-x^n}{\Delta x}=\lim_{\Delta x \to 0} \frac{x^n+nx^{n-1}\Delta x+\frac{n(n-1)}{2} x^{n-2}\Delta x^2+...+\Delta x^n-x^n}{\Delta x}$

其中 $x^n$ 被消掉， $\frac{nx^{n-1} \Delta x}{\Delta x}=nx^{n-1}$ ，其余均乘无穷小 $x_0$ 的正整数幂的项为0；

$\alpha$ 为实数时，

代入，提公因式： $\lim_{\Delta x \to 0} \frac{(x+\Delta x)^\alpha-x^\alpha}{\Delta x}=\lim_{\Delta x \to 0}\frac {x^{\alpha}}{x}\times \frac{(1+\Delta x/x)^{\alpha}-1}{\Delta x/x}$

等价无穷小化简： $=\lim_{\Delta x \to 0}x^{\alpha-1}\times\frac{\alpha (\Delta x/x)}{\Delta x/x}=\alpha x^{\alpha-1}$

$(a^x)'=a^xlna$ ；

代入公式，提公因式： $\lim_{\Delta x \to 0} \frac{(a)^{x+\Delta x}-a^x}{\Delta x}=\lim_{\Delta x \to 0}a^x\times \frac{(a)^{\Delta x}-1}{\Delta x}$

等价无穷小公式化简： $=\lim_{\Delta x \to 0}a^x\times \frac{\Delta xlna}{\Delta x}=a^xlna$

$(log_ax)'=\frac{1}{xlna}$ ，特别地 $(ln|x|)'=\frac{1}{x}$ ；

代入，对数性质化简： $\lim_{\Delta x \to 0} \frac{log_a(x+\Delta x)-log_ax}{\Delta x}=\lim_{\Delta x \to 0}\frac{1}{\Delta x}log_a(1+\frac{\Delta x}{x})$

等价无穷小： $=\lim_{\Delta x \to 0}\frac{1}{x}\frac{x}{\Delta x}log_a(1+\frac{\Delta x}{x})=\lim_{\Delta x \to 0}\frac{1}{x}\frac{log_a(1+\frac{\Delta x}{x})}{\frac{\Delta x}{x}}=\frac{1}{x}lna$

$(sin(x))'=cos(x)$ ， $(cos(x))'=-sin(x)$ ；

代入公式，和差化积展开：

$\lim_{\Delta x \to 0} \frac{sin(x+\Delta x)-sinx}{\Delta x}=\lim_{\Delta x \to 0}\frac{sin(x)cos(\Delta x)+cos(x)sin(\Delta x)-sinx}{\Delta x}$

前项为零x无穷小=0，后项等价无穷小公式化简：

围观大佬们的花式解法，打开崭新世界：sinx求导为什么是cosx？ - 知乎

$(tan(x))'=sec^2(x)$ ， $(cot(x))'=-csc^2(x)$ ；

化为sinx/cosx，采用商的求导法则可证：

$(tan(x))'=(\frac{sin(x)}{cos(x)})'=\frac{sin'(x)cos(x)-cos'(x)sin(x)}{cos^2(x)}=\frac{1}{cos^2(x)}=sec^2(x)$

$(sec(x))'=sec(x)tan(x)$ ， $(csc(x))'=-csc(x)cot(x)$ ；

化为1/cosx，采用商的求导法则可证：

$(sec(x))'=(\frac{1}{cos(x)})'=\frac{(1)'cos(x)-cos'(x)1}{cos^2(x)}=\frac{sin(x)}{cos^2(x)}=tan(x)sec(x)$

$(arcsin(x))'=\frac{1}{\sqrt{1-x^2}}$ ， $(arccos(x))'=-\frac{1}{\sqrt{1-x^2}}$ ；

x=siny，利用反函数求导法则可证：

$(arcsin(x))'=\frac{1}{(sin(y))'}=\frac{1}{cos(y)}=\frac{1}{\sqrt{1-sin^2y}}=\frac{1}{\sqrt{1-x^2}}$

$(arctan(x))'=\frac{1}{1+x^2}$ ， $(arccot(x))'=-\frac{1}{1+x^2}$ ；

x=tany，利用反函数求导法则可证：

$(arctan(x))'=\frac{1}{(tan(y))'}=\frac{1}{sec^2(y)}=\frac{1}{1+tan^2(y)}=\frac{1}{1+x^2}$

例题【2015年数二 10题】高阶函数求导

例题【2022年数三 13题】复合函数求导

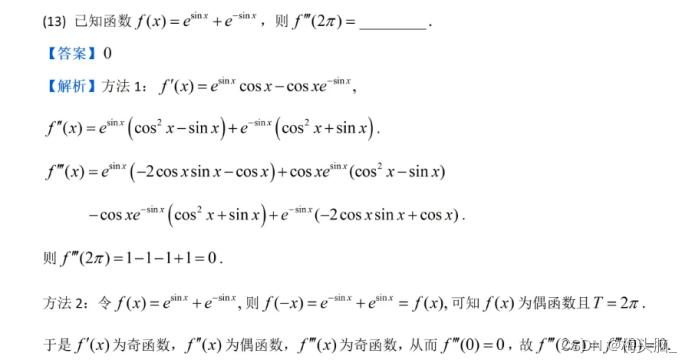
🍂 计算题目类型2，隐函数求导数：

$F(x,y)=0$ 【直角方程】
普通函数：恒等式左右两边求导，得到 $F[x,y(x)]\equiv0$ ；
幂指函数： $y=u(x)^{v(x)}$ 可以化为对数 $\ln y=v(x) \ln u(x)$ 求导。
$\begin{cases}x=\phi(t) \\ y=\psi(t)\\\end{cases}$ 【参数方程】

一阶可导：根据复合函数与反函数的求导法则， $\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\phi'(t)}{\psi'(t)}$

二阶可导：根据复合函数与反函数的求导法则， $\frac{\mathrm{d}^2y}{\mathrm{d}x^2}=\frac{\phi''(t)\psi'(t)-\phi'(t)\psi''(t)}{\psi'^2(t)}\cdot\frac{1}{\psi'(t)}$

注意：参数方程是近年的高频考点，求二阶导数容易只写 $\frac{\phi''(t)\psi'(t)-\phi'(t)\psi''(t)}{\psi'^2(t)}$ ，遗漏 $\frac{1}{\psi'(t)}$ ；因为这是对t求导二阶导数，而不是对x求二阶导数，所以在商导时要记住分母x的方程也含有t哦~~

例题【2020年数一 13题】参数函数求导

🍃微分中值定理

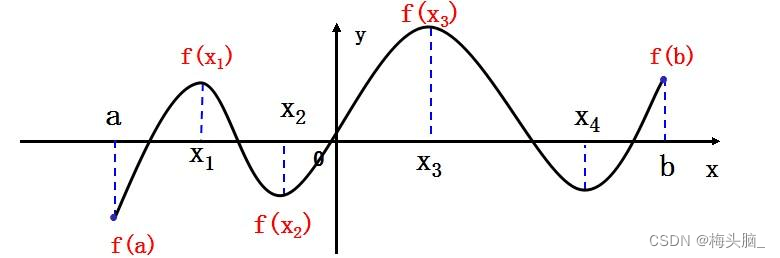
🍂基本介绍

这里省略复杂的定义[毕竟已经在思维导图中写过一遍啦]，借图快速复习~

图源Curren：高数第3章微分中值定理及导数应用 - 知乎 (zhihu.com)

罗尔中值定理简述：区间端点A、B相等，连续曲线f(x)，区间内总有1点[记为 $\xi$ ]的切线斜率=0；

拉格朗日中值定理简述：区间端点A、B，连续曲线f(x)，区间内总有1点[记为 $\xi$ ]的切线斜率为=区间端点AB连线斜率；

柯西中值定理简述：可以近似看作参数方程版本的拉格朗日中值定理；当F(x)=x时，柯西中值定理便转化为拉格朗日中值定理~

🍂证明题目

🍂证明题目类型1，求方程的根

证明有根存在：
适合方程系数已知或可以估算f(x)的极限正负值：找出方程f(a)>0及f(b)<0的两点，根据零点定理可证明方程在(a,b)有根；[零点定理在本系列第一章有介绍]
适合方程系数未知或可以推算F(x)在两点处为零：记F’(x)=f(x)，根据题目条件，找到a、b两点使F(a)=F(b)，根据罗尔定理可证明F’(x)即f(x)在(a,b)有根；
证明根的个数：
将方程记为函数，求导，解出f’(x)=0的点，根据方程单调性判定根的个数~

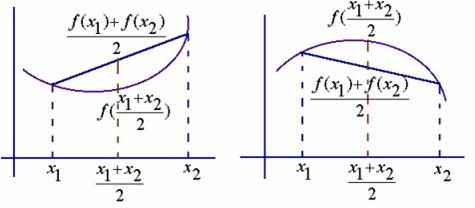
🍂证明题目类型2，证明不等式

两个常见结论
$sin(x)<x<tan(x),x\in (0,\frac{\pi}{2})$ ，在证明第一个重要极限时采用几何法证明：
画1/4单位圆，OA的长度为1，设角度DOB为x，则弧线AC根据弧长公式为x，AB为sinx，AD为tanx[🌸数学中的tan是什么意思？_百度知道 (baidu.com)]，由S▲OBA＜S扇形OBA<S▲OCD可推结论~
图源cabrnary：两个重要极限- 知乎 (zhihu.com)

$\frac{x}{1+x}<ln(1+x)<x,x>0$ ，证明过程如下：
根据题目条件，可以设公式 $f(t)=ln(1+t)$ ，并能够确定区间 $[0,x]$ ；

列拉格朗日中值定理的等式： $\frac{f(x)-f(0)}{x-0}=f'(\xi)$ ，并同时可求出 $f'(\xi)=(ln(1+t))'|_{t=\xi}=\frac{1}{1+\xi}$ ；

将函数值，导数值代回拉格朗日中值定理的等式： $ln(1+x)=\frac{x}{1+\xi},\xi\in [0,x]$

$\xi$ 代入端点值，原题可证。

例题【2022年数一 4题】

🍂证明题目类型3，中值定理证明

构造辅助函数，通过证明辅助函数的中值定理来间接证明原函数的中值定理；
采用反证法，假设结论不成立，然后推出矛盾，从而证明结论成立；
利用函数的单调性、凸凹性、极值等性质，结合中值定理的条件进行证明；
将原函数进行泰勒展开，利用展开式中的多项式性质，结合中值定理的条件进行证明。

例题【2013年数三 10题】

🍃函数的应用

🍂选填题目

🍂选填题目类型1：计算渐近线

水平渐近线： $\lim_{x\to +\infty}f(x)=A,\lim_{x\to -\infty}f(x)=A$
铅直渐近线： $\lim_{x\to x_0+}f(x)=\infty,\lim_{x\to x_0-}f(x)=\infty$

斜渐近线： $\lim_{x\to +\infty}\frac{f(x)}{x}=a,\lim_{x\to -\infty}\frac{f(x)}{x}=a$

例题【2023年数一 1题】计算渐近线

🍂选填题目类型2：导数的几何意义：切线方程、法线方程

计算切线斜率与法线斜率，然后使用点斜式列直接方程：
直角坐标：

斜线斜率： $f'(x_0)$

法线斜率： $-\frac{1}{f'(x_0)}$

参数方程：

切线斜率： $\frac{dy/dt}{dx/dt}$

极坐标方程：和我一样傻傻不会求极坐标方程的小伙伴可以转参数方程

转化方程： $\begin{cases}x=f(\theta) cos(\theta) \\y=f(\theta) sin(\theta)\\\end{cases}$

计算弧长与曲率公式：