柏林噪声（Perlin Noise）的matlab实现

柏林噪声（Perlin Noise）的matlab实现

柏林噪声是1983年Ken Perlin提出的噪声，用于模拟自然纹理，比如水波，手绘，火焰，大理石等纹路，也可以生成残蚀效果动态烟雾等各种常见特效。

根据计算机噪声产生的方法，可以分为梯度噪声和数值噪声，而柏林噪声就是梯度噪声最典型的代表之一。其中本文的算法和思路都来自于下面这篇博客，有兴趣的可以认真看一看这篇博客的内容。
【图形学】谈谈噪声

下面介绍一下一维、二维以及更高维度下柏林噪声（Perlin Noise）的matlab实现。

1.二维柏林噪声

二维柏林噪声是柏林噪声的基础，理解了二维柏林噪声之后有助于更快的实现其它维度的噪声。

算法的思路如下：

生成晶格点矩形网格
生成计算点网格，计算点网格范围要小于晶格点网格，而且要比晶格点网格更密。
给晶格点网格的格点生成随机单位圆梯度
分别计算每个计算点的数值：
	确定计算点在在晶格中的位置，寻找该点所在的矩形网格的4个角点（晶格点）
	分别计算每个角点对该计算点的影响：
		计算该点与角点之间的方向向量
		用方向向量与角点（晶格点）的梯度向量做点积
	对四个点进行加权，得到该计算点的数值，使得数值在区域内平缓过渡
绘制噪声图谱

接下来用图片来介绍一下算法的实现思路：

分别计算4个角点对该点的梯度影响：


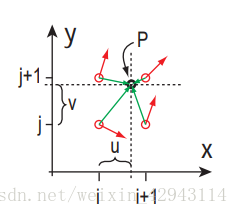
实际计算中，取整数点作为晶格点，用来生成各个梯度向量。其中u,v代表计算点的小数点部分，即x-floor(x)和y-floor(y)。之后用方向向量分别和对应的四个角点的梯度值做点积，生成n00, n10,n01和n11。n00代表和矩形左下角↙的梯度点的点积，n10代表右下角↘的点积，n01代表和左上角↖的点积，n11代表和右上角↗的点积。g代表各对应角点的梯度向量。

之后四个值加权处理。加权采用先x加权，后y加权。即先利用n00和n10加权为n0，再利用n01和n11加权为n1，这一步是x加权；之后再利用n0和n1加权为n，这一步是y加权。加权公式为：
$$n_0=n_{00}(1-f(u))+n_{10}f(u)$$
$$n_1=n_{01}(1-f(u))+n_{11}f(u)$$
$$n=n_0(1-f(u))+n_{1}f(u)$$
一般$f(u)$取$f(0)=0，f(0.5)=0.5，f(1)=1$的函数，低阶的可以取$f(u)=u$，高阶的可以取：
$f(u)=3u^2-2u^3$或者   f ( u ) = 6 u 5 − 15 u 4 + 10 u 3 \ f(u)=6u^5-15u^4+10u^3  f(u)=6u5−15u