手写机器学习算法系列——层次聚类算法(二)

最新推荐文章于 2025-01-22 19:23:39 发布

木有鱼丸223

最新推荐文章于 2025-01-22 19:23:39 发布

阅读量785

点赞数 13

分类专栏：手写机器学习算法系列文章标签：机器学习算法聚类

本文链接：https://blog.csdn.net/weixin_42973210/article/details/139482587

版权

手写机器学习算法系列专栏收录该内容

7 篇文章

订阅专栏

1. 层次聚类算法简介

层次聚类算法是一种通过计算不同样本之间的相似度，然后根据相似度进行聚类的算法。它的核心思想可以分为两类：凝聚型和分裂型。其和分割型聚类算法区别如下所示：
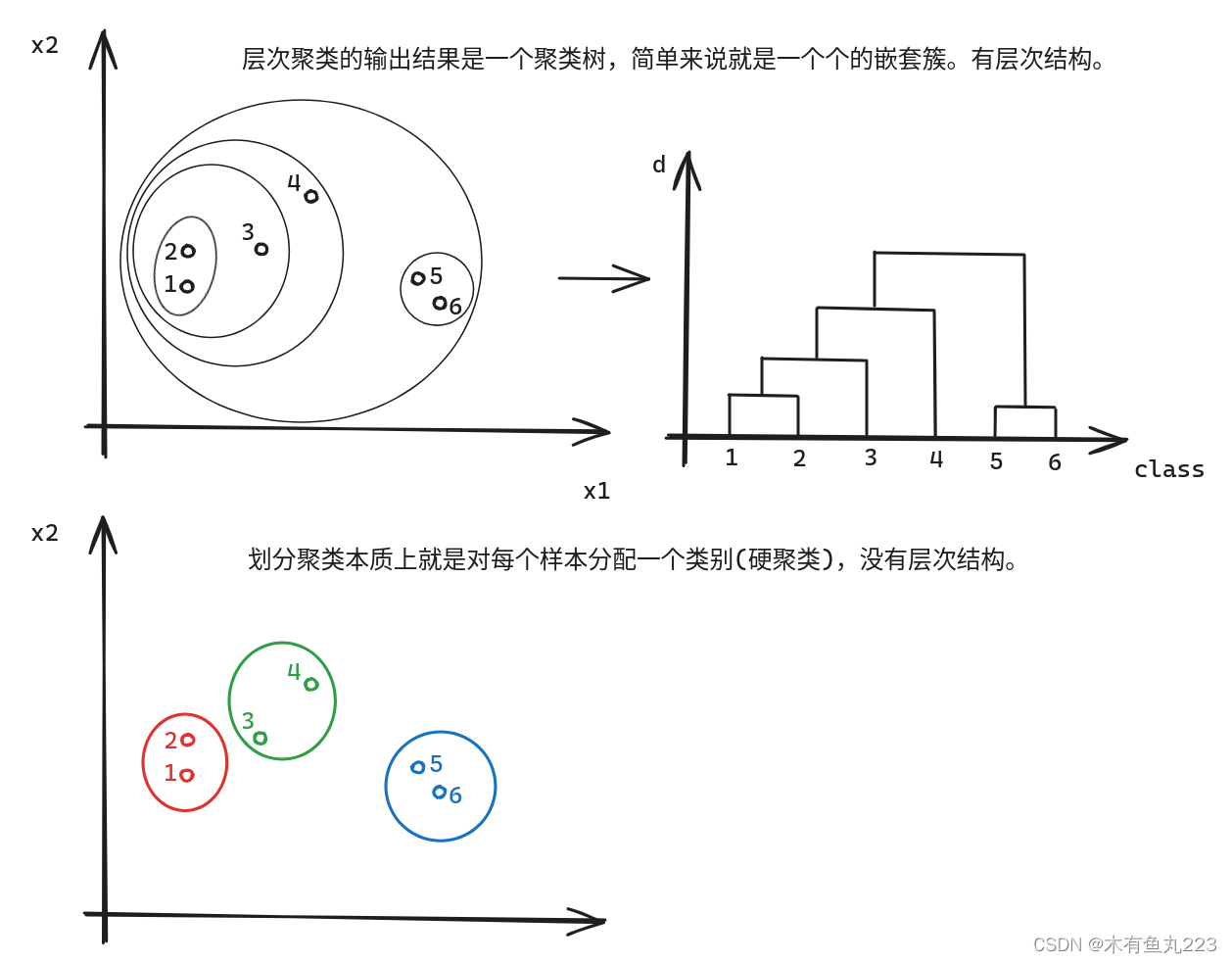
在这里插入图片描述
凝聚型聚类（Agglomerative Clustering）：这种方法开始时，每个对象单独成为一类，然后在算法运行的过程中，逐渐把相似度高的类聚集在一起，直到满足停止条件（如类的个数达到用户的预设值）。
分裂型聚类（Divisive Clustering）：与凝聚型聚类相反，分裂型聚类开始时，所有对象都属于一个类，然后在算法运行过程中，逐渐把类分裂成多个小类，直到满足停止条件。
在这里插入图片描述

2. 常用的层次聚类算法

2.1 基于K-Means的分裂型聚类算法

利用 K-Means 算法分割方法：

把数据集归为单个类别作为顶层‘’
使用 K-Means 算法把划分成 2 个子类别，构成子层；

可递归使用 K-Means 算法继续划分子层到终止条件。
在这里插入图片描述
这种分裂型聚类算法有个很大的缺点就是，在上一层中被分为两类的样本点，无论距离多么接近，后续都不可能被划分为同一个簇内。其次是，这种方式计算量巨大。

2.2 凝聚型层次聚类算法

这个算法流程可以描述为以下图示：
在这里插入图片描述
首先对于所有样本点来说，根据两点之间的距离可以定义一个距离矩阵(对角线和左下角均没有)，然后找到表格中最小距离(5和6)，将之归类为G1，然后更新表格。其中左上角表示1到G1距离的定义 $d(1,G1)=min\{d(1,5),d(1,6)\}$ （以最小距离作为簇之间的距离）。更新完表格之后，迭代执行，直到表格没有了，按顺序就完成了凝聚型层次聚类算法，结果见上图右下。

这里有两个问题：1、样本与样本之间的距离如何定义？2、样本与簇之间的距离如何定义？(不使用最小距离)。根据不同的定义，就可以定义出来不同的算法，这里简单提一下。再深入，就很复杂了，包括使用怎样的数据结构，怎样记录聚类进程等，写完了我也记不住，本博客仅仅是为了介绍算法的基本思想。
在这里插入图片描述

3. 代码分享

3.1 代码结果

在这里插入图片描述

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import linkage, dendrogram, fcluster
from sklearn.metrics.cluster import adjusted_mutual_info_score


if __name__ == '__main__':
    center = [[1,1],[-1,-1],[1,-1]]
    X, labels = make_blobs(n_samples = 1000, centers = center, cluster_std = 0.4, random_state = 0)

    plt.figure(figsize=(8,6))
    plt.scatter(X[:,0], X[:,1], c = 'black')
    plt.title("data distrabute")
    
    Z = linkage(X, method = 'ward', metric = 'euclidean')
    print(Z.shape)
    
    plt.figure(figsize=(8,6))
    dendrogram(Z, truncate_mode = 'lastp', p = 20, show_contracted=False, leaf_rotation=90, leaf_font_size=15, show_leaf_counts=True)
    
    labels_pred = fcluster(Z, t=25, criterion='distance')
    print(labels_pred[0:100])
    print(len(set(labels_pred)))

    plt.figure(figsize=(8,6))
    plt.scatter(X[:,0], X[:,1], c = labels_pred, cmap='prism')

    score = adjusted_mutual_info_score(labels, labels_pred)
    print('Adjust mutual information : {}'.format(score))
    plt.show()