自然语言处理(NLP)-2.3 自动补全与语言模型(Autocomplete and Language Models)

1.N-Grams语言模型概述

1.1 基本概念

    定义：一个N-gram就是一个由句子中连续单词构成的序列，其中N表示该序列中单词个数

    三种常见n-gram：

            Unigrams：一个单词构成一个序列

            Bigrams：两个连续单词构成一个序列

            Trigrams：三个连续单词构成一个序列

        例：

            

    功能：

        (1)计算句子概率

        (2)根据上文来估计下一个单词的概率

        

    应用：

        语言识别、拼写纠正、辅助沟通系统...

        

    句子自动补全：

        (1)对文本进行预处理，使其适用于N-gram模型

        (2)处理字典外单词

        (3)平滑处理

        (4)语言模型评估

        

1.2 N-grams与概率

    序列表示：

        定义：用表示句子中的第i个单词，以此来代指整个句子

           

        表示方法： ，上标 i 表示序列长度；下标 j 表示起始位置

        例：即表示从句子中第一个单词开始，取之后连续m个单词

            

    概率计算：

        (1)Unigram概率计算：

            方法：单词出现次数 / 句子长度，即单个单词的出现概率

               

            例：

               

        (2)Bigram概率：

            方法：两个单词一起出现的次数除前一个单词出现的次数

                

            例：

               

        (3)Trigram概率：

            方法：三个单词一起出现的次数除前两个单词一起出现的次数

               

            例：

               

        (4)N-gram probability：

            方法：n个单词一起出现的次数除前n-1个单词一起出现的次数

               

1.3 序列概率(Sequence Probabilities)

    序列概率：

        功能：计算整个句子(序列)的概率

           

        方法：根据链式法则，依次计算条件概率

           

        例：

           

        问题：句子较长部分可能不在语料库中，因此其出现次数为0，导致整个句子概率为0

           

    马尔可夫假设：

        定义：对于一个句子概率，只有最后N个单词重要，因此可以只考虑最后N个单词来近似计算整个句子的概率

        功能：近似计算整个句子的概率，从而解决上述问题

        

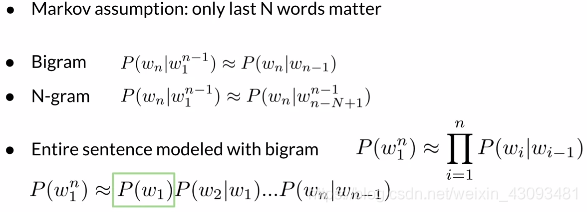
        例：

           

1.4 起始符与终止符

    起始符：

        功能：统一计算方法，使得无需对第一个单词进行单独计算

            

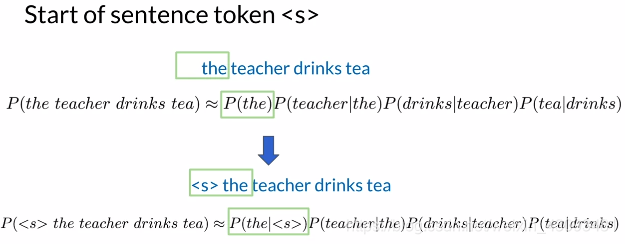
        方法：N-gram模型中，前加N-1个起始符

            

    终止符：

        方法：不管N为多少，只在句尾加一个终止符

            

    例子：

        包含起始符与终止符情况下计算句子概率

       

---

2.N-Gram语言模型的构建与评估

2.1 整体流程

    整体流程：

        构建计数矩阵

        构建概率矩阵

        构建语言模型

        引入对数概率

        应用语言模型生成句子

        

2.2 具体流程

    (1)构建计数矩阵：

        方法：统计各n-gram出现次数

        

    (2)构建概率矩阵：

        方法：将计数矩阵中各元素除以各行总数和得到概率矩阵

        

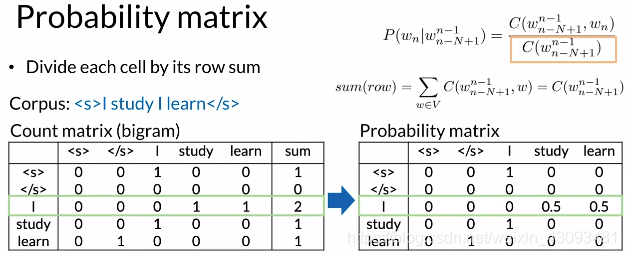
    (3)概率矩阵与语言模型：

        方法：通过概率矩阵，即可计算句子概率和下一个单词的概率

        

    (4)对数概率：

        原因：计算中很多<1的数连乘，可能造成数值下溢，因此使用对数概率避免该问题

        

    (5)应用语言模型生成句子：

        方法：选择起始符，通过概率矩阵选择下一个概率最高词，直到选择了终止符，句子生成结束

        

2.3 模型评估

    测试集：

        定义：将语料库划分为训练集与测试集

            

        拆分方法：

            (1)连续划分

            (2)随机划分

            

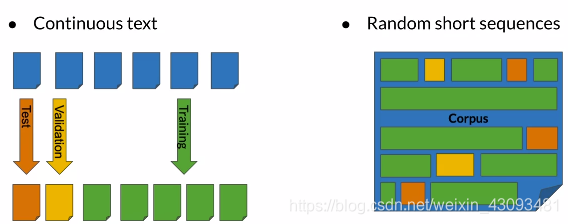
    困惑度(Perplexity)：

        定义：一种评价句子语义清晰度的指标，困惑度越小句子语义越清晰，模型越好

        计算方法：

                

        例：bigram的困惑度计算

            

        性质：

            

        例子：

            

    对数困惑度(Log perplexity)：

        定义：对困惑度取对数

        计数方法：

            

    例子：

        可以看出N越大句子的困惑度越小，其语义越清晰

           

---

3.特殊情况处理

3.1 对词汇表外单词的处理

    未知词：

        定义：不存在于字典中的词

        解决：使用<UNK>标识符代替

            

    未知词处理：

        步骤：

            (1)创建词汇表

            (2)对于未知词(即不在词汇表中的词)，使用<UNK>标识符代替

            (3)计算<UNK>和其他词的概率

            

        例子：

            

    构建词汇表：

        规定最小词频：即一个单词最少要在语料库中出现多少次才能被加入词汇表

        

3.2 对不存在序列的处理

    原因：

        不存在的N-grams会导致出现0，又由于进行连乘操作会使最终句子概率变为0

            

    平滑法(Smoothing)：

        方法：通过分子分母同加一个数来进行平滑，消除出现0的可能

            

    回退法(Backoff)：

        方法：当n-gram找不到时，进行回退，找(n-1)-gram

           

    插值法(Interpolation)：

        方法：给不同的n-gram设置不同的权重，且各之和为1，n越大权重越大，用加法代替连乘

           

---

项目代码：https://github.com/Ogmx/Natural-Language-Processing-Specialization

可将代码与数据下载至本地，使用jupyter notebook打开