逆矩阵的定义
A为n阶方阵,存在n阶方阵B,使得AB=BA=E,则A的逆矩阵A-1=B,且可证矩阵的逆唯一。
定理: A可逆的充分必要条件是|A|≠0,则:
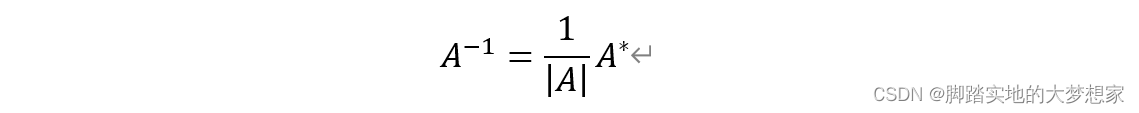
求逆矩阵的方法
- 伴随矩阵法
- 初等变换法
伴随矩阵法
e.g. 通过伴随矩阵求逆矩阵
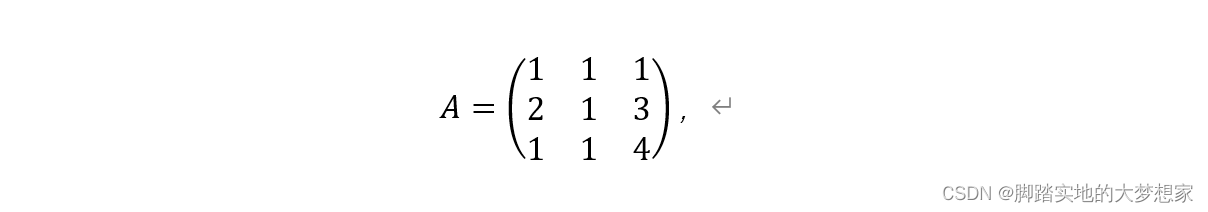
解:
第一步:求A的行列式的值不为0:

第二步:求代数余子式

第三步:求伴随矩阵

第四步:求逆矩阵

矩阵方程&初等变换法
e.g. 矩阵方程:求x


矩阵初等运算的四点注意事项
1)提取出公因子时候要注意提取的方向;
2)A-2不可以,矩阵要与矩阵做加减,所以为A-2E;
3)矩阵永远不要放在分母位置上;
4)一定要先判定可逆,才可以同时左右乘以一个矩阵的逆。
5)待定法可以考虑电脑做。
逆矩阵的性质
A可逆,那么A的逆也可逆,且A逆的逆为A。

若A和B都可逆,那么AB也可逆,且(AB)的逆为B逆A逆。

A可逆,那么A的转置也可逆,且A转置的逆等于A逆的转置
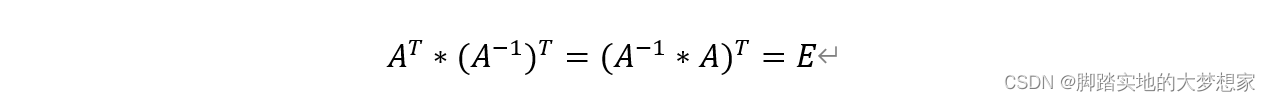
k≠0,(kA)的逆等于1/k乘以A的逆

A可逆,那么A逆的行列式等于A行列式的逆

A可逆,A的伴随矩阵也可逆,且A伴随矩阵的逆等于A的行列式分之一乘以A

























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










