机器学习理论知识要点总结-线性回归和逻辑回归

机器学习理论知识要点总结-线性回归和逻辑回归

作者本是一个转行机器学习的小白，在七月在线学习，接触了一系列机器学习中的模型、参数、算法等内容，现在还不是拎得很清楚，所以收集资料写此博客。旨在加深对算法及优化方法，损失函数及参数的理解。

线性模型:

线性模型形式简单，易于建模，但却蕴含着机器学习中一些重要的基本思想。许多功能更为强大的非线性模型(nonlinear model)可在线性模型的基础上通过引入层级结构或高维映射而得。

线性回归(linear regression)：连续值预测问题。

线性回归试图学得一个线性模型以尽可能准确地预测实值输出标记。
线性回归试图学得: $f(x_i)=w{x}_i+b,使得f(x_i)\simeq y_i$
函数模型:
考虑两个变量:
$$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2$$

$$h_{\theta }(x)=\sum _{i=1}^n{\theta }_i{x}_i={\theta }^{T}x$$

假设函数$f$为输入$x$的线性函数:
$$f(x)={\theta }_0{x}_0+{\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n$$

写成向量形式(在特征x中增加一维$x_0=1$，表示截距项):
$$f(x)={\theta }^{T}x$$

线性回归损失函数:平方损失(Quadratic loss function)

损失函数是修正最后的目标，在线性回归问题中，平方损失是凸函数，可以很好地用梯度下降法求得全局最小值点。

我们需要找到最好的权重/参数$[{\theta }_0,{\theta }_1,{\theta }_2,...,{\theta }_n]=\theta$
我们需要定义损失函数为:
$$J({\theta }_0,{\theta }_1,{\theta }_2,...,{\theta }_n)=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$

我们现在需要做的就是让损失函数最小，即最小化损失函数。

梯度下降GD(Gradient Descent)

梯度下降是优化算法的一种，是逐步最小化损失函数的过程。
$${\theta }_1:={\theta }_1-\alpha \frac{d}{d{\theta }_1}J({\theta }_1)$$

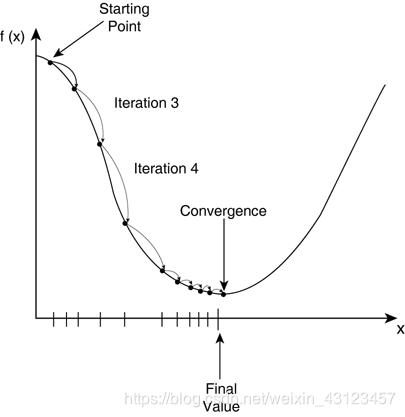
对于多元化情况的梯度下降：
$$h_{\theta }(x)={\theta }_0+{\theta }_{1}x$$

损失函数为：
$$j({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$

对损失函数求导，沿着负梯度方向进行迭代，得出:${\theta }_0,{\theta }_1$
$${\theta }_0:={\theta }_0-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})$$

$${\theta }_1:={\theta }_1-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\cdot x^{(i)}$$

假如有n个特征/变量$x_j$(j=1···n):
$${\theta }_j:={\theta }_j-\alpha \frac{d}{d{\theta }_j}J({\theta }_0,{\theta }_1)$$

梯度下降中的学习率

其中$\alpha$为学习率：在梯度下降中为“步长”。在上图中，我们我们找准方向，迈出一步，直至山底。
$\alpha$学习率太大，可能导致算法震荡甚至不收敛。
$\alpha$学习率太小，可能导致算法收敛过慢，迭代很多次。
工业界中，我们只需要找一个差不多的$\alpha$即可。
$\alpha$不需要设定逐步变小或者衰减，因为点沿着负梯度方向迈一小步的同事，斜率会的绝对值越来越小，趋于0。所以$\alpha$不变的情况下， 步子会越来越小。

逻辑回归(logistic regression)也称对数几率回归(西瓜书)：分类问题。

逻辑回归在工业界中也常用作排序，因为其输出为每一类的概率大小。
线性回归在分类问题上健壮性很差，容易受噪声影响。
为什么逻辑回归叫回归，却可以做对离散值预测等分类问题。因为逻辑回归回归的是概率。
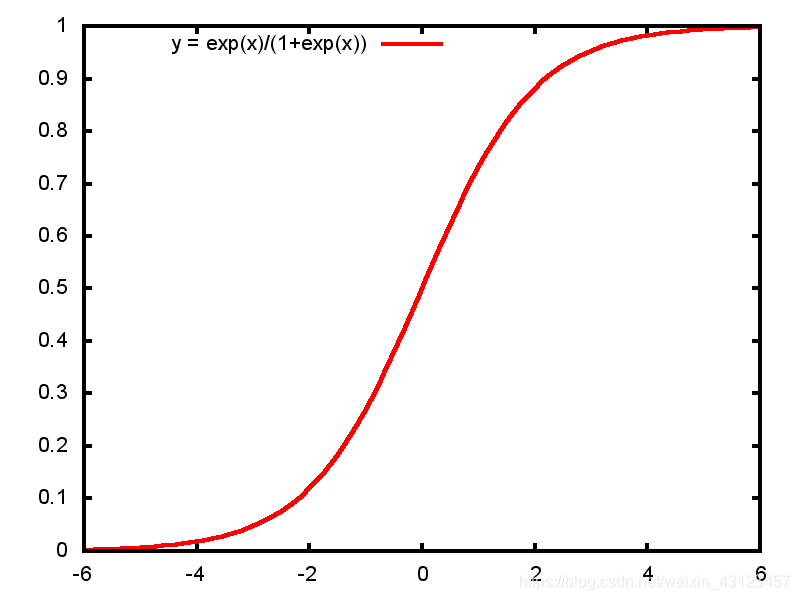
这也归功于sigmoid函数(也叫S型函数、压缩函数)
让我们一起认识一下sigmoid函数:
$$g(x)=\frac{1}{1+e^{-x}}$$

sigmoid函数拥有良好的数学特性：
比如求导时:$g^{\prime }(x)=g(x)(1-g(x))$
函数图像为:

逻辑回归:寻找判定边界/决策边界

决策边界在二维空间中可能是一个曲线，在高维空间中也可能是一个曲面。
逻辑回归表达式：
$$h_{\theta }(x)=g(-{\theta }^{T}x)=\frac{1}{1+e^{-{\theta }^{T}x}}$$

当$x_0=1$时，表达式就转化为:
$${\theta }^{T}x={\theta }_0+\sum _{j=1}^n{\theta }_j{x}_j$$

逻辑回归损失函数:对数损失(log loss)

如果我们用线性回归的损失函数(平方损失)，我们会拿到一个非凸的函数，非凸函数除去全局最低点，还有很多局部最低点，我们用梯度下降拿到的可能是局部最低点。这不是我们想要的结果。所以我们希望损失函数是凸函数。
对数损失函数：和标准的差异度有多高，是凸函数。每个样本都计算出一个损失，m个样本求出m个损失，求和再做平均
$$J(\theta )=\frac{1}{m}\sum _{i=1}^{m}Cost(h_{\theta }(x^{(i)}),y^{(i)})$$

$$J(\theta )=-\frac{1}{m}[\sum _{i=1}^m{y}^{(i)}log(h_{\theta }(x^{(i)}))+(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]$$

加入正则化项:$\frac{\lambda }{2m}{\sum }_{j=1}^n{\theta }_j^2$
$$J(\theta )=[-\frac{1}{m}[\sum _{i=1}^m{y}^{(i)}log(h_{\theta }(x^{(i)}))+(1-y^{(i)})log1-h_{\theta }(x^{(i)})]]+\frac{\lambda }{2m}\sum _{j=1}^n{\theta }_j^2$$

梯度下降求梯度：$\alpha$同为 learning rata “步长”

$${\theta }_j:={\theta }_j-\alpha \frac{\delta }{\delta {\theta }_j}J(\theta )$$

总结

1.模型本身并无好坏之分。
2.LR可以概率的形式输出结果，而非只是0,1判断。
3.LR可解释性强，可控度高。
4.训练快，特征处理之后更快。
5.输出的结果可以排序。