B e t a Beta Beta分布
众所周知,当一个随机变量
Y
Y
Y的密度函数如下所示时,称这个变量
Y
Y
Y满足
B
e
t
a
(
a
,
b
)
Beta(a,b)
Beta(a,b)分布:
f
(
y
)
=
y
a
−
1
(
1
−
y
)
b
−
1
∫
0
1
y
a
−
1
(
1
−
y
)
b
−
1
d
y
=
y
a
−
1
(
1
−
y
)
b
−
1
B
(
a
,
b
)
f(y)=\frac{y^{a-1}(1-y)^{b-1}}{\int_0^1{y^{a-1}(1-y)^{b-1}dy}}=\frac{y^{a-1}(1-y)^{b-1}}{B(a,b)}
f(y)=∫01ya−1(1−y)b−1dyya−1(1−y)b−1=B(a,b)ya−1(1−y)b−1
其中:
B
(
a
,
b
)
=
∫
0
1
y
a
−
1
(
1
−
y
)
b
−
1
d
y
B(a,b)={\int_0^1{y^{a-1}(1-y)^{b-1}dy}}
B(a,b)=∫01ya−1(1−y)b−1dy是
B
e
t
a
Beta
Beta函数。
然而,令人困惑不解的是,这个 B e t a ( a , b ) Beta(a,b) Beta(a,b)分布中的参数 a , b a,b a,b到底是什么含义?而对于满足这个分布的变量 Y Y Y,它又有着什么实际意义?接下来我所要阐明的就是这个问题,更好的理解所谓 B e t a ( a , b ) Beta(a,b) Beta(a,b)分布。
1.二项分布
首先,从随机变量 Y Y Y的密度函数 y a − 1 ( 1 − y ) b − 1 ∫ 0 1 y a − 1 ( 1 − y ) b − 1 d y \frac{y^{a-1}(1-y)^{b-1}}{\int_0^1{y^{a-1}(1-y)^{b-1}dy}} ∫01ya−1(1−y)b−1dyya−1(1−y)b−1我们可以看出,分母部分是分子部分的从0到1的积分,证明这个 Y Y Y的取值范围是[0,1],那么我们这时候会不会自然而然地想到,这个 Y Y Y很有可能代表的就是一个概率呢?
从这个角度出发,是不是看着 y a − 1 ( 1 − y ) b − 1 {y^{a-1}(1-y)^{b-1}} ya−1(1−y)b−1也觉得有点眼熟呢?没错,对于一个服从于二项分布 B ( n , p ) B(n,p) B(n,p)的随机变量 ξ \xi ξ,它的分布列为 P ( ξ = k ) = C n k p k ( 1 − p ) n − k P(\xi=k)=C_n^kp^k(1-p)^{n-k} P(ξ=k)=Cnkpk(1−p)n−k,这与服从于 B e t a Beta Beta分布的 Y Y Y的密度函数 f ( y ) f(y) f(y)中的 y a − 1 ( 1 − y ) b − 1 {y^{a-1}(1-y)^{b-1}} ya−1(1−y)b−1有着异曲同工之妙!那么 B e t a Beta Beta分布与二项分布之间是否存在着什么联系?
2.贝叶斯
上面已经说过,对于一个服从于二项分布 B ( n , p ) B(n,p) B(n,p)的随机变量 ξ \xi ξ,它的分布列为 P ( ξ = k ) = C n k p k ( 1 − p ) n − k P(\xi=k)=C_n^kp^k(1-p)^{n-k} P(ξ=k)=Cnkpk(1−p)n−k二项分布 B ( n , p ) B(n,p) B(n,p)是独立重复 n n n次伯努利实验,每次事件发生的概率都为 p p p,所以 ξ \xi ξ实质上是在已经确定参数 p p p的条件下,事件发生的次数之和,所以分布列 P ( ξ = k ) P(\xi=k) P(ξ=k)也可以记为: P ( ξ = k ∣ p ) = C n k p k ( 1 − p ) n − k P(\xi=k|p)=C_n^kp^k(1-p)^{n-k} P(ξ=k∣p)=Cnkpk(1−p)n−k可以看出,这是一个条件概率。
熟悉贝叶斯思想与原理的朋友都知道,在贝叶斯公式中,后验概率可以由先验概率和条件概率一同得到: P ( B i ∣ A ) = P ( A ∣ B i ) P ( B i ) ∑ j = 1 m P ( A ∣ B j ) P ( B j ) P(B_i|A)=\frac{P(A|B_i)P(B_i)}{\sum_{j=1}^mP(A|B_j)P(B_j)} P(Bi∣A)=∑j=1mP(A∣Bj)P(Bj)P(A∣Bi)P(Bi)在已经知道参数先验分布信息与样本信息的情况下,我们也可以应用贝叶斯公式得到参数的后验分布信息: π ( θ ∣ x ) = L ( x ∣ θ ) π ( θ ) ∫ Θ L ( x ∣ θ ) π ( θ ) d θ \pi(\theta|x)=\frac{L(x|\theta)\pi(\theta)}{\int_\Theta L(x|\theta)\pi(\theta)d\theta} π(θ∣x)=∫ΘL(x∣θ)π(θ)dθL(x∣θ)π(θ)这里, θ \theta θ表示需要估计的未知参数, x x x表示样本信息, π ( θ ) \pi(\theta) π(θ)表示 θ \theta θ的先验密度函数, L ( x ∣ θ ) L(x|\theta) L(x∣θ)表示 x x x关于 θ \theta θ的条件密度函数, Θ \Theta Θ表示参数 θ \theta θ的取值空间。
在这里,我们可能会奇怪,为什么 x x x关于 θ \theta θ的条件密度函数要用 L ( x ∣ θ ) L(x|\theta) L(x∣θ)表示,这是因为在我们使用极大似然法进行参数估计的时候,已知样本信息 x x x,需要选择合适的参数 θ \theta θ使发生样本所代表事件的概率最大,所以 L ( x ∣ θ ) L(x|\theta) L(x∣θ)在这里是一个似然函数。
假设随机变量
X
X
X服从二项分布
B
(
n
,
θ
)
B(n,\theta)
B(n,θ),那么似然函数:
L
(
x
∣
θ
)
=
P
(
X
=
x
∣
θ
)
=
C
n
x
θ
x
(
1
−
θ
)
n
−
x
L(x|\theta)=P(X=x|\theta)=C_n^x\theta^x(1-\theta)^{n-x}
L(x∣θ)=P(X=x∣θ)=Cnxθx(1−θ)n−x如果我们对参数
θ
\theta
θ一无所知,那么对
θ
\theta
θ的先验分布
π
(
θ
)
\pi(\theta)
π(θ)可以做如下均匀分布的假设,假设
θ
\theta
θ~
U
(
0
,
1
)
U(0,1)
U(0,1),这个假设也称为贝叶斯假设:
π
(
θ
)
=
1
(
0
<
θ
<
1
)
\pi(\theta)=1~~~(0<\theta<1)
π(θ)=1 (0<θ<1)
=
0
(
e
l
s
e
)
=0~~~(else)
=0 (else)由以上似然函数和参数的先验分布可以得出参数的后验分布:
π
(
θ
∣
x
)
=
L
(
x
∣
θ
)
π
(
θ
)
∫
Θ
L
(
x
∣
θ
)
π
(
θ
)
d
θ
\pi(\theta|x)=\frac{L(x|\theta)\pi(\theta)}{\int_\Theta L(x|\theta)\pi(\theta)d\theta}
π(θ∣x)=∫ΘL(x∣θ)π(θ)dθL(x∣θ)π(θ)
=
C
n
x
θ
x
(
1
−
θ
)
n
−
x
∫
0
1
C
n
x
θ
x
(
1
−
θ
)
n
−
x
d
θ
~~~~~~~~~~~~~~~~~~~~=\frac{C_n^x\theta^x(1-\theta)^{n-x}}{\int_0^1C_n^x\theta^x(1-\theta)^{n-x}d\theta}
=∫01Cnxθx(1−θ)n−xdθCnxθx(1−θ)n−x
=
θ
x
(
1
−
θ
)
n
−
x
∫
0
1
θ
x
(
1
−
θ
)
n
−
x
d
θ
~~~~~~~~~~~~~~~=\frac{\theta^x(1-\theta)^{n-x}}{\int_0^1\theta^x(1-\theta)^{n-x}d\theta}
=∫01θx(1−θ)n−xdθθx(1−θ)n−x
=
θ
(
x
+
1
)
−
1
(
1
−
θ
)
(
n
−
x
+
1
)
−
1
B
(
x
+
1
,
n
−
x
+
1
)
~~~~~~~~~~~~~~~~~~~~~~~~~=\frac{\theta^{(x+1)-1}(1-\theta)^{(n-x+1)-1}}{B(x+1,n-x+1)}
=B(x+1,n−x+1)θ(x+1)−1(1−θ)(n−x+1)−1
显然有:
θ
∣
x
\theta|x
θ∣x ~
B
e
t
a
(
x
+
1
,
n
−
x
+
1
)
Beta(x+1,n-x+1)
Beta(x+1,n−x+1)
π
(
θ
∣
x
)
=
θ
(
x
+
1
)
−
1
(
1
−
θ
)
(
n
−
x
+
1
)
−
1
B
(
x
+
1
,
n
−
x
+
1
)
\pi(\theta|x)=\frac{\theta^{(x+1)-1}(1-\theta)^{(n-x+1)-1}}{B(x+1,n-x+1)}
π(θ∣x)=B(x+1,n−x+1)θ(x+1)−1(1−θ)(n−x+1)−1
再回到刚开始的服从于贝塔分布的随机变量 Y Y Y进行比对:
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Y
Y
Y~
B
e
t
a
(
a
,
b
)
Beta(a,b)
Beta(a,b)
f
(
y
)
=
y
a
−
1
(
1
−
y
)
b
−
1
∫
0
1
y
a
−
1
(
1
−
y
)
b
−
1
d
y
=
y
a
−
1
(
1
−
y
)
b
−
1
B
(
a
,
b
)
f(y)=\frac{y^{a-1}(1-y)^{b-1}}{\int_0^1{y^{a-1}(1-y)^{b-1}dy}}=\frac{y^{a-1}(1-y)^{b-1}}{B(a,b)}
f(y)=∫01ya−1(1−y)b−1dyya−1(1−y)b−1=B(a,b)ya−1(1−y)b−1
我们可以看出,贝塔分布里的参数 a a a就相当于参数估计中的 x + 1 x+1 x+1;贝塔分布里的参数 b b b就相当于 n − x + 1 n-x+1 n−x+1。
3.参数意义
上面我们假设随机变量
X
X
X服从二项分布
B
(
n
,
θ
)
B(n,\theta)
B(n,θ),现在我们给这个二项分布赋予一个实际意义:假设今年武汉一共出生了
n
n
n个婴儿,
θ
\theta
θ为出生婴儿性别为女的概率,那么
X
X
X就是武汉今年所出生女婴的总数,经统计,武汉今年一共出生了
x
x
x个女婴。按照经典的统计思想,可以用频率估计概率,那么女婴出生的概率
θ
^
=
x
n
\hat{\theta}=\frac{x}{n}
θ^=nx。
但根据贝叶斯的观点,
θ
\theta
θ存在着一个分布,密度函数是
π
(
θ
∣
x
)
=
θ
(
x
+
1
)
−
1
(
1
−
θ
)
(
n
−
x
+
1
)
−
1
B
(
x
+
1
,
n
−
x
+
1
)
\pi(\theta|x)=\frac{\theta^{(x+1)-1}(1-\theta)^{(n-x+1)-1}}{B(x+1,n-x+1)}
π(θ∣x)=B(x+1,n−x+1)θ(x+1)−1(1−θ)(n−x+1)−1,我们可以看一下这个分布到底是怎样的。
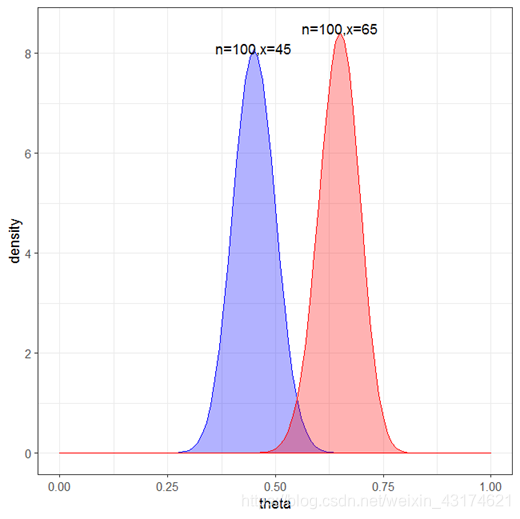
分别取
n
=
100
,
x
=
45
n=100,x=45
n=100,x=45 (
a
=
46
,
b
=
56
a=46,b=56
a=46,b=56),以及
n
=
100
,
x
=
65
n=100,x=65
n=100,x=65 (
a
=
66
,
b
=
36
a=66,b=36
a=66,b=36),画出的密度函数如下图所示:
p=ggplot(data.frame(x=c(0,1)),aes(x=x))+
stat_function(fun=dbeta,args=list(shape1=46,shape2=56),
geom="area",fill="blue",alpha=0.3,colour="blue")+
stat_function(fun=dbeta,args=list(shape1=66,shape2=36),
geom="area",fill="red",alpha=0.3,colour="red")+
annotate("text",x=0.45,y=8.1,label="n=100,x=45")+
annotate("text",x=0.65,y=8.5,label="n=100,x=65")+
labs(x="theta",y="density")
p_remove_bg=p+theme_bw()
p_remove_bg
正如我们所看到的,横坐标值所代表的是女婴出生率,纵坐标代表的是密度函数,红色和蓝色所代表的随机变量分别服从 B e t a ( 46 , 56 ) Beta(46,56) Beta(46,56)与 B e t a ( 66 , 36 ) Beta(66,36) Beta(66,36),从分布上来看,红色所代表的女婴出生率要高于蓝色所代表的女婴出生率。至此,服从贝塔分布的随机变量的意义,以及贝塔分布中的参数的实际意义得到了一定的解释。
4. B e t a Beta Beta分布
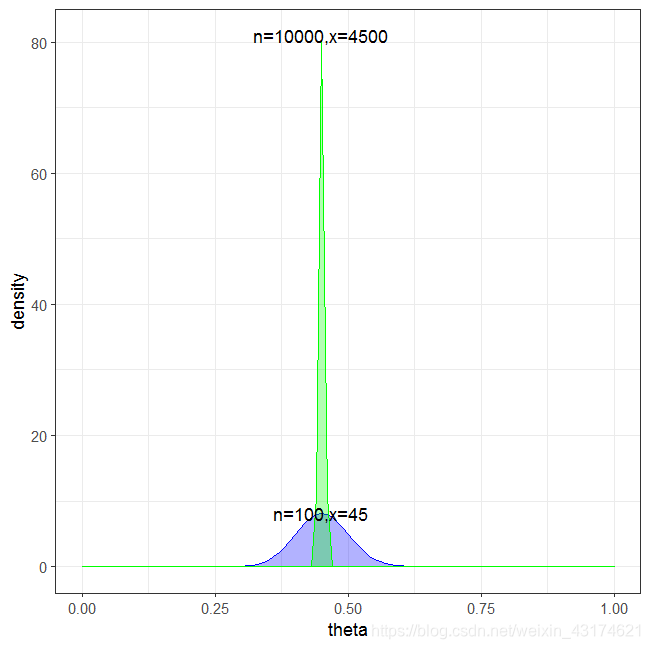
上面我们假设 n = 100 , x = 45 n=100,x=45 n=100,x=45很明显不符合实际,因为武汉每年出生的婴儿量是很大的,如果我们扩大样本量,那么参数 θ \theta θ的后验分布会不会有所变化呢?我们将 n n n调整为10000, x x x调整为4500, ( a = 4501 , b = 5501 ) (a=4501,b=5501) (a=4501,b=5501):
很明显可以看出,扩大样本量时,参数估计的众数基本不变(即密度函数最大的点所对应的值),而方差缩小了很多,所以扩大样本量可以使估计更为精确。
5.共轭先验分布
回顾一下,随机变量 X X X~ B ( n , θ ) B(n,\theta) B(n,θ) , 参数的先验信息为: θ \theta θ~ U ( 0 , 1 ) U(0,1) U(0,1),给出样本信息 x x x,那么参数的后验分布为 θ ∣ x \theta|x θ∣x~ B e t a ( x + 1 , n − x + 1 ) Beta(x+1,n-x+1) Beta(x+1,n−x+1)。
当随机变量 Y Y Y~ B e t a ( 1 , 1 ) Beta(1,1) Beta(1,1)时, B e t a Beta Beta分布退化为均匀分布, Y Y Y~ U ( 0 , 1 ) U(0,1) U(0,1)。
所以参数 θ \theta θ的分布实质上是由先验的 θ \theta θ~ B e t a ( 1 , 1 ) Beta(1,1) Beta(1,1) 变为后验的 θ ∣ x \theta|x θ∣x~ B e t a ( x + 1 , n − x + 1 ) Beta(x+1,n-x+1) Beta(x+1,n−x+1)。 π ( θ ) \pi(\theta) π(θ)与 π ( θ ∣ x ) \pi(\theta|x) π(θ∣x)属于同一分布族。我们称该 B e t a Beta Beta分布族为 θ \theta θ的共轭先验分布族。
结论: 对于服从二项分布
B
(
n
,
θ
)
B(n,\theta)
B(n,θ)的随机变量
X
X
X而言, 样本信息为
x
x
x,假设
θ
\theta
θ的先验分布满足
θ
\theta
θ~
B
e
t
a
(
a
,
b
)
Beta(a,b)
Beta(a,b), 经过简单的推导可得,
θ
\theta
θ的后验分布满足
θ
∣
x
\theta|x
θ∣x~
B
e
t
a
(
x
+
a
,
n
−
x
+
b
)
Beta(x+a,n-x+b)
Beta(x+a,n−x+b)。





















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








