SLAM与李群李代数

概念

1. 群是什么？
   官方概念：是一种集合加上一种运算的代数结构，且该运算满足“封结幺逆”四个性质
   例如：
   旋转矩阵满足一下性质
   $$R{R}^T=I,det(R)=1$$
   那么可以得到一个旋转矩阵集合
   $$SO(3)=\left\{R\in {\Re }^{3\times 3}|R{R}^T=I,det(R)=1\right\}$$
   但是这是对加法不封闭的
   $$R_1+R_2\notin SO(3)$$
   但是这是对乘法是封闭的
   $$R_1\cdot R_2\in SO(3)$$
   同时旋转矩阵的运算（$\cdot$）又满足“封结幺逆”四个性质，那么就说这是一个群（特殊正交群）

同理变换矩阵集合也是满足群的概念（特殊欧式群）
$$SE(3)=\left\{T=\left|\begin{array}{cc}R& t\\ 0& 1\end{array}\right|\in {\Re }^{4\times 4}|R\in SO(3)\right\}$$

2. 李群是什么？
   是指一个具有连续（光滑）性质的群
   可以想象一个刚体在空间中旋转平移，实际上就是一个连续的过程，所以说SO(3) SE(3)是李群

3. 李代数是什么
   李群都有与之对应的李代数，李代数描述了李群的局部性质。
   由于这方面知识比较复杂，并没有去深究其性质，这里暂时先知道，李群和李代数是一个映射关系
   例如SO(3)
   $$R=exp({\varphi }^{\wedge })$$
   $$so(3)=\left\{\varphi \in {\Re }^3|\Phi ={\varphi }^{\wedge }\in {\Re }^{3\times 3}\right\}$$

SE(3)
$$se(3)=\left\{\xi =\left|\begin{array}{c}\rho \\ \varphi \end{array}\right|\in {\Re }^6,\rho \in {\Re }^3,\varphi \in so(3),{\xi }^{\wedge }=\left|\begin{array}{cc}{\varphi }^{\wedge }& \rho \\ o^T& 1\end{array}\right|\in {\Re }^{4\times 4}\right\}$$

李群与李代数的映射关系

SO(3)上

我们知道指数的泰勒展开为

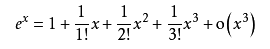
那么任意矩阵的指数映射可以写成
$$exp(A)=\sum _{n=0}^{\infty }\frac{1}{n!}{A}^n$$
假设A矩阵对应的李代数是$\varphi$
$$exp({\varphi }^{\wedge })=\sum _{n=0}^{\infty }\frac{1}{n!}({\varphi }^{\wedge }{)}^n$$

其实$\varphi$是一个三维向量，那把它转化成角轴，记为$\theta$和$a$，于是有$\varphi =\theta a$
其中$a$是旋转轴，并且长度为1,对于$a^{\wedge }$有以下性质
$$a^{\wedge }{a}^{\wedge }=a^{\wedge }{a}^T-I$$
$$a^{\wedge }{a}^{\wedge }{a}^{\wedge }=-a^{\wedge }$$
把指数映射进行泰勒展开后化简
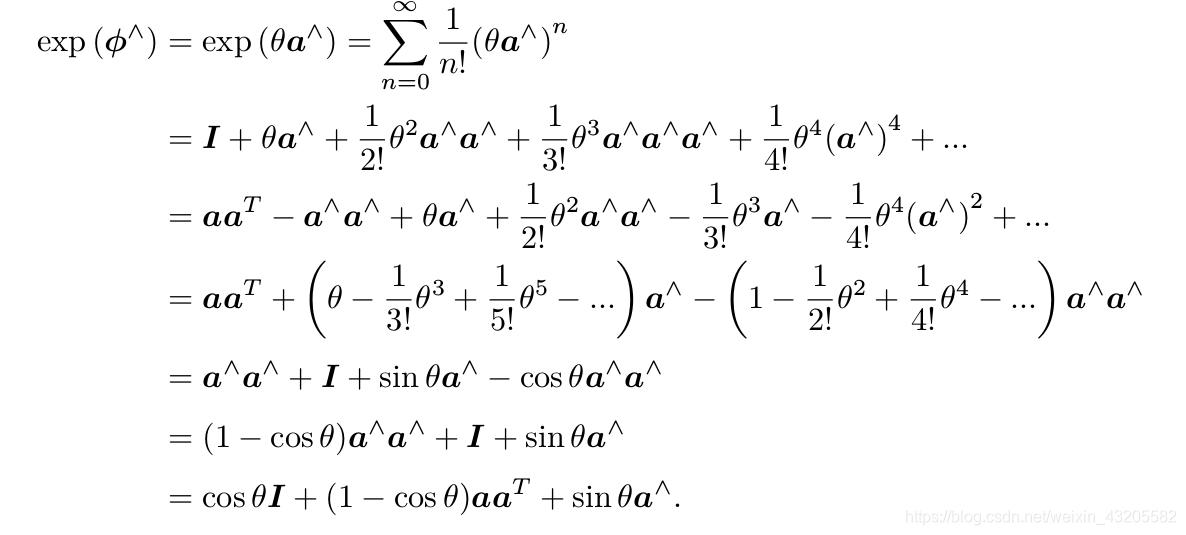得到的结果其实就是罗德里格斯公式，就是旋转矩阵R，从这里可以看到，旋转矩阵对应的李代数实际上就是旋转向量

SE(3)上

$$exp({\xi }^{\wedge })=\left|\begin{array}{cc}{\sum }_{n=0}^{\infty }\frac{1}{n!}({\varphi }^{\wedge }{)}^n& {\sum }_{n=0}^{\infty }\frac{1}{(n+1)!}({\varphi }^{\wedge }{)}^n\rho \\ 0^T& 1\end{array}\right|$$
其中平移向量引入了一个雅克比矩阵$J$

那么$J$就可以得到式子

$$J=\frac{sin\theta }{\theta }I+(1-\frac{sin\theta }{\theta })a{a}^T+\frac{1-cos\theta }{\theta }{a}^{\wedge }$$
所以SE(3）的指数映射右上角的t就满足
$$t=J\rho$$
那么在已知变换矩阵$T$的情况下J可以由$\varphi$得到，那么$\rho$就可以由上面线性方程得出
最后
$$exp({\xi }^{\wedge })=\left|\begin{array}{cc}R& J\rho \\ 0^T& 1\end{array}\right|=T$$

变换关系表

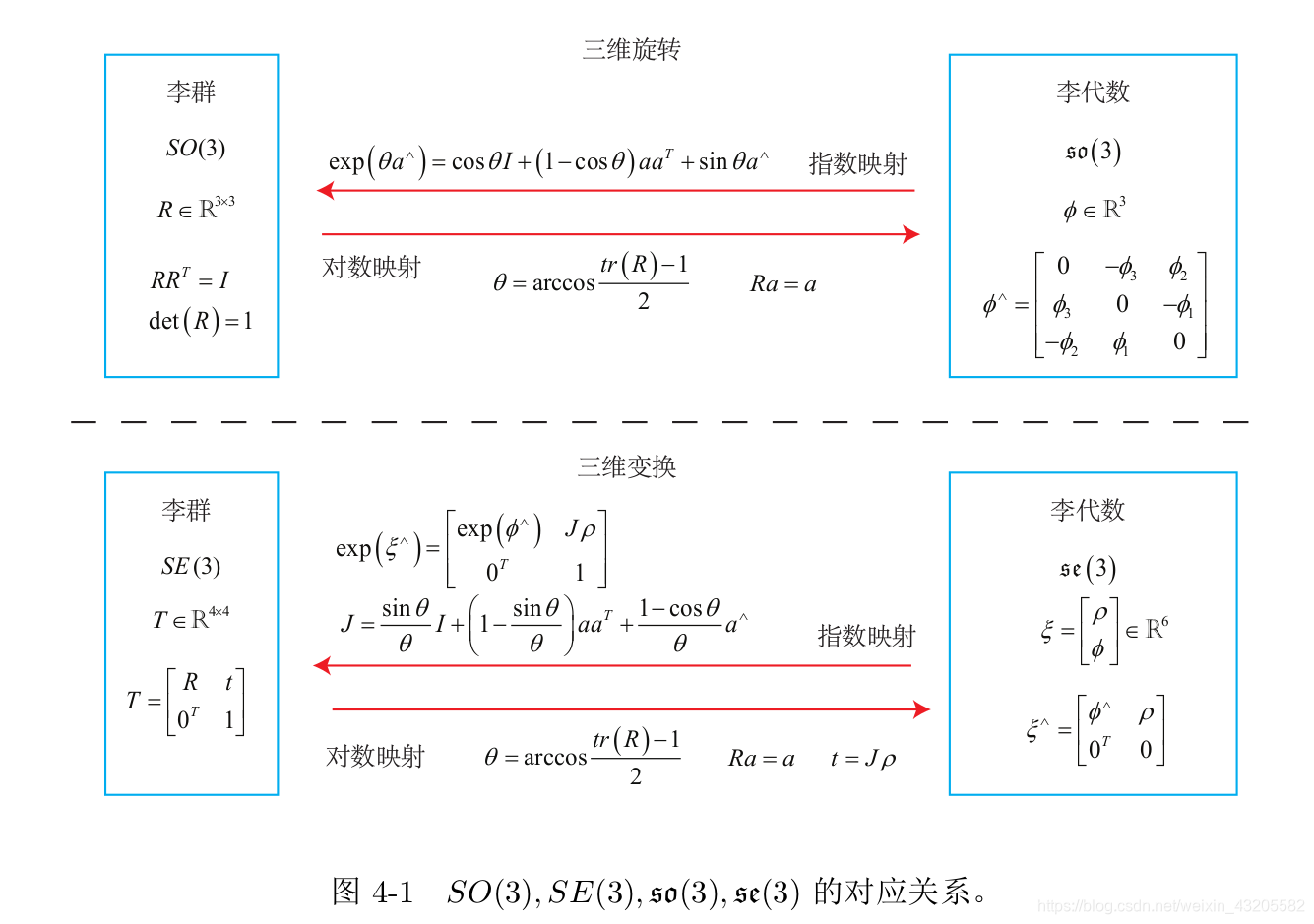
以上就是解释了旋转矩阵变换矩阵可以构成李群，并解释了李群和李代数的对映关系，同样给出了计算过程，仅此而已，并又有太多的和SLAM进行关联结合。

李代数的求导与扰动模型

这一部分才是真正的李群李代数和SLAM理论进行结合。目前的SLAM主流是非线性优化，也就是构造成最小二乘的形式，利用迭代求解相机的pose，这里的优化变量是T，所以需要对矩阵进行求导，但是我们知道这是对加法不封闭的，也就不能直接利用矩阵进行增量加减完成求导，但是在对应的李代数空间里面，两两相加其中一个是小量的情况下可以近似李群空间上的相加（引入一个雅克比矩阵），这样就可以对矩阵进行求导了。

• 实际上在讨论李群空间的矩阵相乘是否等价于李代数空间的两向量相加
  $$exp({\varphi }_1^{\wedge })exp({\varphi }_2^{\wedge })=exp(({\varphi }_1+{\varphi }_2{)}^{\wedge }))$$
  或者说是
  $$ln(exp({\varphi }_1^{\wedge })exp({\varphi }_2^{\wedge }))=A+B$$

如果AB是标量的话就是可以成立的，但是矩阵是不成立的，会得到很多有李括号的余项。
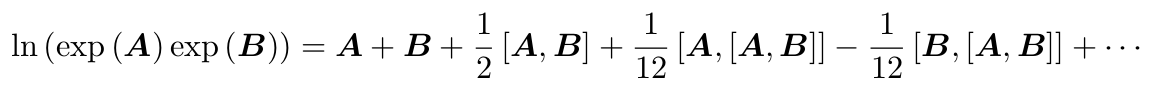这叫做BCH（Baker-Campbell-Hausdorff）公式

可以考虑采用近似的方式，当A或者B对应的李代数${\varphi }_1$或者${\varphi }_2$其中一个是小量的时候（求导时就是其中一个为小量），可以把二次以上的项都忽略掉，直接的得到
$$ln(exp({\varphi }_1^{\wedge })exp({\varphi }_2^{\wedge }){)}^{\vee }\simeq \{\begin{array}{l}{J}_l({\varphi }_2{)}^{-1}{\varphi }_1+{\varphi }_2当{\varphi }_1为小量\\ J_r({\varphi }_1{)}^{-1}{\varphi }_2+{\varphi }_1当{\varphi }_2为小量\end{array}$$

从该式可以看到，当一个旋转矩阵$R_2$左乘一个微小旋转矩阵$R_1$时，可以近似看做在原有李代数${\varphi }_2$上加上了一项$J_l({\varphi }_2{)}^{-1}{\varphi }_1$。同样如果是右乘的话，当一个旋转矩阵$R_1$右乘一个微小矩阵$R_2$，可以近似看做在原有李代数${\varphi }_1$上加上了一项$J_r({\varphi }_1{)}^{-1}{\varphi }_2$
目前没有去了解相关的证明，所以这里就直接给出了一个近似结论
其中$J_l$和上面证明求出的$J$是一样的形式
$$J_l=J=\frac{sin\theta }{\theta }I+(1-\frac{sin\theta }{\theta })a{a}^T+\frac{1-cos\theta }{\theta }{a}^{\wedge }$$
它的逆
$$J_l^{-1}=\frac{\theta }{2}cot\frac{\theta }{2}I+(1-\frac{\theta }{2}cot\frac{\theta }{2})a{a}^T+\frac{\theta }{2}{a}^{\wedge }$$
右乘雅克比仅需要对自变量取负号
$$J_r(\varphi )=J_l(-\varphi )$$

• 讨论李群乘法和李代数加法的关系
  上面的过程就是在证明李群乘法和李代数加法的关系的可行性
  假设$\Delta \varphi$是微小量，进行左乘在某个旋转量$\varphi$，由李群上的乘法转变成李代数的加法
  $$exp(\Delta {\varphi }^{\wedge })exp({\varphi }^{\wedge })=exp((\varphi +J_l(\varphi {)}^{-1}\Delta \varphi {)}^{\wedge })$$

因为$\Delta \varphi$是小量，那$J_l(\varphi {)}^{-1}\Delta \varphi$也是小量，$\Delta \varphi \simeq J_l(\varphi {)}^{-1}\Delta \varphi$，所以SO(3)上左右乘微小量近似于so(3)上加进行微小量相加
同样的由李代数上的加法转变成李群上的左乘和右乘
由
$$exp(\Delta {\varphi }^{\wedge })exp({\varphi }^{\wedge })=exp((J_l(\varphi {)}^{-1}\Delta \varphi +\varphi {)}^{\wedge })$$
$$exp({\varphi }^{\wedge })exp(\Delta {\varphi }^{\wedge })=exp((J_r(\varphi {)}^{-1}\Delta \varphi +\varphi {)}^{\wedge })$$
左边到右边就是在小量上乘上雅克比逆矩阵，右边到左边就在小量上乘上雅克比正矩阵，同样的可以推导
$$exp((\Delta \varphi +\varphi {)}^{\wedge })=exp((J_l(\varphi )\Delta \varphi {)}^{\wedge })exp({\varphi }^{\wedge })=exp({\varphi }^{\wedge })exp((J_r(\varphi )\Delta \varphi {)}^{\wedge })$$

那么对于$SE(3)$也是同样结论
$$exp(\Delta {\xi }^{\wedge })exp({\xi }^{\wedge })=exp((J_l(\xi {)}^{-1}\Delta \xi +\xi {)}^{\wedge })$$
$$exp({\xi }^{\wedge })exp(\Delta {\xi }^{\wedge })=exp((J_r(\xi {)}^{-1}\Delta \xi +\xi {)}^{\wedge })$$
这里的J是6*6的矩阵，比较复杂

以上就是通过近似的方式，使得李群上的小量相乘与李代数空间上相加进行相关联，那么这样就可以实现矩阵的求导

矩阵的求导

求导这里可以有两种方法

1. 直接用李代数表示位姿，然后根据李代数加法来对李代数求导（这个更贴近于求导规则）
2. 对李群左右乘微小扰动，对扰动求导，称为左右扰动模型（前面已经解释，SO(3)上左右乘微小扰动近似于so(3)上加微小量）

方法一 李代数求导

从上面证明可以看到使用该方法不管是左乘还是右乘都会引入一个雅克比矩阵，所以需要另外计算这个复杂的雅克比矩阵

方法二 扰动模型

设扰动$\Delta R$对应的李代数是$\Delta \varphi$
左乘
$$\begin{gathered} \frac{\partial Rp}{\partial \varphi }=\underset{\Delta \varphi \to 0}{\lim }\frac{exp((\Delta \varphi {)}^{\wedge })exp({\varphi }^{\wedge })p-exp({\varphi }^{\wedge })p}{\Delta \varphi } \\ =\underset{\Delta \varphi \to 0}{\lim }\frac{(I+\Delta {\varphi }^{\wedge })exp({\varphi }^{\wedge })p-exp({\varphi }^{\wedge })p}{\Delta \varphi } \\ =\underset{\Delta \varphi \to 0}{\lim }\frac{\Delta {\varphi }^{\wedge }exp({\varphi }^{\wedge })p}{\Delta \varphi } \\ =\underset{\Delta \varphi \to 0}{\lim }-\frac{(Rp{)}^{\wedge }\Delta \varphi }{\Delta \varphi } \\ =(Rp{)}^{\wedge } \end{gathered}$$
右乘
$$\begin{gathered} \frac{\partial Rp}{\partial \varphi }=\underset{\Delta \varphi \to 0}{\lim }\frac{exp({\varphi }^{\wedge })exp((\Delta \varphi {)}^{\wedge })p-exp({\varphi }^{\wedge })p}{\Delta \varphi } \\ =\underset{\Delta \varphi \to 0}{\lim }\frac{exp({\varphi }^{\wedge })(I+\Delta {\varphi }^{\wedge })p-exp({\varphi }^{\wedge })p}{\Delta \varphi } \\ =\underset{\Delta \varphi \to 0}{\lim }\frac{exp({\varphi }^{\wedge })\Delta {\varphi }^{\wedge }p}{\Delta \varphi } \\ =\underset{\Delta \varphi \to 0}{\lim }-\frac{R{p}^{\wedge }\Delta \varphi }{\Delta \varphi } \\ =R{p}^{\wedge } \end{gathered}$$
对于SE(3)上的扰动模型求导
左乘
$$\begin{gathered} \frac{\partial Tp}{\partial \xi }=\underset{\Delta \xi \to 0}{\lim }\frac{exp((\Delta \xi {)}^{\wedge })exp({\xi }^{\wedge })p-exp({\xi }^{\wedge })p}{\Delta \xi } \\ =\underset{\Delta \xi \to 0}{\lim }\frac{(I+\Delta {\xi }^{\wedge })exp({\xi }^{\wedge })p-exp({\xi }^{\wedge })p}{\Delta \xi } \\ =\underset{\Delta \xi \to 0}{\lim }\frac{\Delta {\xi }^{\wedge }exp({\xi }^{\wedge })p}{\Delta \xi } \\ =\underset{\Delta \xi \to 0}{\lim }\frac{\left|\begin{array}{cc}\Delta {\varphi }^{\wedge }& \Delta \rho \\ 0^T& 1\end{array}\right|\left|\begin{array}{c}Rp+t\\ 1\end{array}\right|}{\Delta \xi } \\ =\underset{\Delta \xi \to 0}{\lim }\frac{\left|\begin{array}{c}\Delta {\varphi }^{\wedge }(Rp+t)+\Delta \rho \\ 0\end{array}\right|}{\Delta \xi } \\ =\underset{\Delta \xi \to 0}{\lim }\frac{\left|\begin{array}{c}-(Rp+t{)}^{\wedge }\Delta \varphi +\Delta \rho \\ 0\end{array}\right|}{\Delta \xi } \\ =\left|\begin{array}{cc}I& -(Rp+t{)}^{\wedge }\\ 0^T& 0^T\end{array}\right| \end{gathered}$$
其中
$$\left|\begin{array}{cc}I& -(Rp+t{)}^{\wedge }\\ 0^T& 0^T\end{array}\right|\left|\begin{array}{c}\Delta \rho \\ \Delta \varphi \end{array}\right|=\left|\begin{array}{c}-(Rp+t{)}^{\wedge }\Delta \varphi +\Delta \rho \\ 0\end{array}\right|$$
$$\left|\begin{array}{c}\Delta \rho \\ \Delta \varphi \end{array}\right|=\Delta \xi$$
右乘同理