推断因果关系理论（inferred causation）（上）

本篇博客的内容主要是对Judea的Causality 一书中第二章前四小节的内容进行梳理。
本人最近才开始研究因果理论，发现因果理论的很多概念在网上并没有中文的说明。为了便于交流与讨论，同时也便于自我梳理与总结，拟将本人阅读过程中的一些理解记录下来，欢迎大家进行学术讨论。
以下内容如有理解不当之处，请各路大神多多指教。

引言

从原始数据中学习因果关系的可能性自休谟时代（1711-1776）以来就一直在哲学家的梦想清单上。这种可能性在20世纪80年代中期进入了形式化处理和可行计算的领域，那时图形和概率依赖性之间的数学关系被揭示出来。本文所描述的方法是Pearl（1988b，第8章）的一个结果，它描述了如果人们对数据生成的基本过程做了一些假设（例如，它有一个树结构），如何从非临时统计数据中推断因果关系。

从较弱的结构假设（例如，一般的有向无环图）推断因果关系的前景促使三所大学进行了平行研究：加州大学洛杉矶分校、卡内基梅隆大学和斯坦福大学。一方面，加州大学洛杉矶分校（UCLA）和卡内基梅隆大学(CMU)的研究小组采用了一种方法，即在数据中搜索揭示底层结构碎片的条件独立模式，然后将这些碎片拼凑在一起，形成一个连贯的因果模型（或一组这样的模型）。另一方面，斯坦福研究小组采用贝叶斯方法，数据用于更新分配给候选因果结构的后验概率（Cooper和Herskovits 1991）这个应该是贝叶斯网络结构学习的K2算法。UCLA和CMU的努力已经导致了相似的理论和几乎相同的发现算法，这些都是在TETRAD II程序中实现的（Spirtes等人。1993年）。此后，许多研究团队一直在采用贝叶斯方法（Singh and Valtorta 1995；Heckerman et al。1994年），现在是几种基于图形的学习方法的基础（Jordan 1998）。

因果建模框架（the causal modeling framework）

因果结构（causal structure）

一组变量V的因果结构是一个有向无环图（DAG），其中每个节点对应于V的一个不同元素，每个链接（link）表示相应变量之间的直接函数关系。

因果结构是“因果模型”的蓝图——它精确地描述DAG中每个变量是如何受其父变量影响的，如(1.40)的结构方程模型。

因果模型（causal model）

因果模型是一对参数$M=<D,{\Theta }_D>$，由一个因果结构D和一组与D相容的参数${\Theta }_D$组成。参数${\Theta }_D$将函数$x_i=f_i(p{a}_i,u_i)$ 分配给每个$X_i\in V$，并将概率测度$P(u_i)$ 分配给每个ui，其中PAi是D中Xi的父项，其中每个Ui是根据$P(u_i)$ 给定的随机干扰，独立于所有其他的u。

一旦形成因果模型M，它就定义了系统变量上的联合概率分布P（M）。这种分布反映了因果结构的一些特征（例如，在给定父节点的值的条件下，每个变量必定独立于祖先节点——注：这是马尔科夫性质）。

（发现输入公式太花时间了，接下来带公式的定义就不翻译了）

模型偏好

原则上，由于变量集V是未知的（注：事实上我们一般只研究观察变量O），所以有无限多的模型符合给定的分布，每个模型调用一组不同的“隐藏”变量，每个模型通过不同的因果关系连接观察到的变量。因此，在不限制模型类型的情况下，科学家无法对现象背后的结构做出任何有意义的断言。例如，每个概率分布$P_{[o]}$都可以由一个结构生成，在该结构中，没有观察到的变量是另一个原因的原因，而是所有变量都是一个潜在的共同原因的结果U。同样，假设V=0，但缺少时间信息，科学家永远不能排除底层结构是一个完整的、无环的、任意排序的图的可能性，这种结构（通过正确的参数选择）可以模拟任何模型的行为，而不管变量排序如何。然而，遵循科学归纳法的标准规范，我们有理由排除任何我们发现与数据同样一致的更简单、更不详尽的理论（见定义2.3.5）。在这个选择过程中幸存下来的理论被称为极小值理论。有了这个概念，我们可以按照如下方式构建推断因果关系的（初步）定义。

推断因果关系（初步）

如果从X到Y的有向路径存在于每一个与数据一致的最小结构中，则称变量X对变量Y有因果影响。

我们认为定义2.3.1是初步的，因为它假定所有变量都是观测到的。接下来的几个定义将最小性的概念推广到具有未观测变量的结构。

潜在结构（latent structure）

潜在结构时一组变量L=<D,O>，其中O是观测变量
（对于因果结构是D，包含所有变量V）

结构偏好（structure preference）

描述两个潜在结构之间的偏好。如果有一个可观察到的依赖关系被L1所允许，而被L2所禁止，L1就不能比L2更优。

极小性（minimality）

也就是说最优的潜在结构就是一个极小的（minimal）

一致性（consistency）

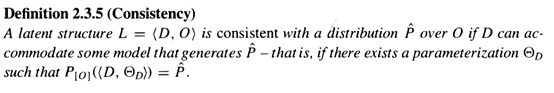
显然，$L$与$\hat{P}$一致的一个必要条件（有时也是充分条件）是，$L$可以解释$\hat{P}$中包含的所有依赖项。

推断因果关系（inferred causation）

给定$\hat{P}$，一个变量C对变量E有因果影响当且仅当在每一个与$\hat{P}$一致的最小潜在结构中，都存在C到E的直接路径。

虽然最小原则（minimality）足以形成推断因果关系的规范理论，但它不能保证实际数据生成模型的结构是最小的，也不能保证在极小结构的广大空间中进行搜索在计算上是切实可行的。一些结构可能会接受一些特殊的参数化，这些参数化将使它们与许多其他具有完全不同结构的最小模型难以区分。

因此，pearl等人提出了一种对分布的限制，称为稳定（stability），也称为DAG-isomorphism或是faithfulness

稳定性

独立性条件指出，当我们将参数从$\Theta$变为${\Theta }^{\prime }$时 ，P中的独立性不会被破坏。
$I(P)$ 表示包含P中所有条件独立关系的集合。
P是一个稳定分布如果存在一个有向无环图D使得对任意变量X,Y,Z,都有 $(X\perp \perp Y|Z{)}_P$ (双向箭头）$(X\perp \perp Y|Z{)}_D$

极小性与稳定性的关系

极小性和稳定性之间的关系可以用下面的类比来说明。假设我们看到一张椅子的图片，我们需要在以下两种理论中做出选择。

• T1：图中的物体是一把椅子。
• T2：图中的物体要么是一把椅子，要么是两把椅子，其中一把把另一把藏起来。

我们对T1的偏爱基于两个原则，一个是基于极小性，另一个是基于稳定性。极小性原则认为，T1优于T2，因为由单个对象组成的场景集是由两个或两个以下对象组成的场景的适当子集，除非我们有相反的证据，否则我们应该选择更具体的理论。稳定性原则先验地排除了T2，认为两个物体不太可能为了让一个物体完美地隐藏另一个物体而彼此对齐，这样的排列是不稳定的。

稳定性的数值例子
对于结构Z<-X->Y，存在模型：

对于所有的函数f1和f2，变量Z和Y在给定X的条件下都是独立的。
相反，如果我们向结构中添加箭头Z -> Y，并使用线性模型


在增加稳定性假设的情况下，只要不存在隐藏变量，每个分布都有一个唯一的最小因果结构（直到d-分离等价）。这种唯一性来自于定理1.2.8，该定理指出两个因果结构是等价的（即，它们可以相互模仿），前提是且仅当它们传递相同的信息依赖性——即，它们具有相同的骨架和相同的v-结构集。

[1] Pearl J. Causality: models, reasoning, and inference[M]. 2000.