统计信号处理基础 习题解答3-3

题目：

观测到数据：

 其中 是具有方差 的WGN，r>0，且是已知的。求A的CRLB，证明有效估计量存在，并求它的方差。对于不同的r值，当N趋于无穷大时，方差会怎样？

---

解答：

根据题目条件，可以得到：

详细求解过程为：

第一步：得到观察量的概率分布函数 

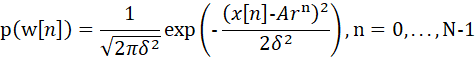
第二步：得到观察量相关的似然函数

 第三步：对似然函数取对数：

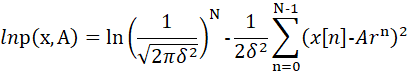
第四步：对取对数后的似然函数求一阶导数，得到：

第五步：对取对数后的似然函数求二阶导数，得到：

 第六步：对二阶导数求数学期望，得到：

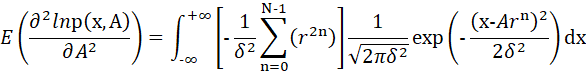
因此，估计量 的CRLB可以表示为：

由于似然函数的一阶导数可以进一步表示为：

也就是可以表示成（3.7）的形式，其中：

因此：

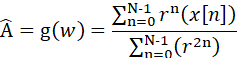
是MVU估计量，其方差为：

---

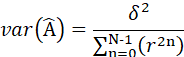
当N趋近于无穷大时，如果 ，那么

 此时

 而如果 时，存在：

此时

---

另外，上述六步求CRLB的过程，也可以直接采用（3.14）结论：

此时：

那么

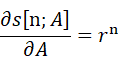
因此，直接带入（3.14），得到：

与上述过程一致，但更加简单高效。