Games101 Geometry 曲线和曲面

---

我们上节课只讨论了关于隐式几何的部分,接下来我们来介绍一下显式几何.

显示几何

显式几何有很多种,例如:
1.三角形面

2.贝塞尔表面

3.细分曲面

4.NURBS

5.点云

…

点云

点云是最简单的物体的面的表示.

点云很简单,我们不考虑物体是一个表面,而是由一堆点形成的,只要点与点之间的距离足够小,我们就不会看到间隙,从而可以看到由一堆点构成的图形,也就是 “表面” 这么一个概念.

一个点的表示在空间中是(X , Y , Z),那么物体实际上就是一个(X,Y,Z)的列表.

如图,这是一个雕塑,在上半部分点云的密度非常大,我们可以看到物体的表面,随着点云密度的降低,下半部分我们可以发现当点云稀疏的时候,我们很难看出这是一个面.

如果用点云来表示一个复杂的模型,我们会需要十分多,十分密集的点来表示物体.

因此只要你的点足够密集,点云几乎可以表示任何几何物体.但是如果点云密度比较低,则会像雕塑的下半部分一样,无法清晰的展示出物体的样子,因此一般情况下我们并不使用点云.除了扫描出来得到的最原始的数据,(通常做一些三维空间中的扫描得到的输出就是一堆点云.)

如图是一个点云的例子,左边是一堆点,我们可以将其变为不同的面,我们用不同的shading方法可以得到不同效果的连续的面.

Polygon Mesh(多边形面)

在图形学中得到最广泛应用的是多边形面这种方法,我们可以将面拆解成若干个小的三角形或者四边形,我们通过用三角形或者四边形的组合去描述各种各样的物体.

接下来我们介绍一下通常在图形学中是如何表示用三角形面形成的物体的,这里展示的是一种特定的文件格式:

这种格式一般一个文件表示一个场景或者物体,这种文件格式叫做Wavefront Object File.这个文件是一个文本文件,它只是将空间中的一堆顶点,法线,纹理坐标分开来表示,然后再将其组织起来形成所需要的模型.

以图中的例子来说,它其实描述的是一个立方体:

立方体在空间中由8个顶点,因此 3 - 10行存储的是顶点的信息.

立方体在空间中由6个面也就是6个法线,因此 27 - 34 行存储的是法线的信息.

12 - 25行存储的是纹理坐标的信息.

在定义好以上信息之后,我们开始定义之间的连接关系,36 - 47行就是这些信息:

f 顶点坐标 / 纹理坐标 / 法线坐标,坐标表示的是在定义的信息中的第几个.

比如 f 5/1/1 1/2/1 4/3/1

我们定义中的第五,第一,第四,这三个顶点构成一个三角形,并且这三个顶点上我们应用第一,第二,第三的纹理坐标,且这三个顶点上的法线是第一个.

其实就是找三个顶点形成一个三角形,然后再找他们的纹理坐标和法线.

Curves(贝塞尔曲线)

图中的海豚是在按照固定轨迹去进行运动的,这个轨迹是一个曲线,也可以让摄像机沿着这个轨迹进行运动,从而产生效果,这就是曲线的一些应用.

贝塞尔曲线

首先我们要明白贝塞尔曲线做了一个什么事情:

我们用一系列的控制点去定义某一曲线,这些控制点可以定义曲线满足的一些性质,

比如说从P0开始并且沿着以P0 P1方向为切线往前走,

曲线在P3处结束,且结束时以P2 P3方向为切线往前走.

这样通过控制点,我们定义了曲线的起点p0和终点p3,且起始的切线和结束的切线一定在p0 p1方向和p2 p3方向,
这样我们通过这四个控制点得到了唯一的曲线:

曲线不一定要经过其他的控制点,但一定要经过起点和终点.

那么如何通过任意多个控制点去画一条的曲线呢?

我们以三个控制点画一条二次贝塞尔曲线(quadratic bezier)为例:

b0为起点,b2为终点,b1决定了它向哪里弯,我们大概能够联想出画出的曲线样子,实际上也确实是差不多的曲线,只是有一个精准的方法去控制它.

也就是我们假设它的起点为时间0,终点为1,我们想要画出这条曲线实际上就是把它在任意一个时间t时这个曲线的点对应在空间中或是平面上的哪个位置给找出来就可以了.

说白了就是给一个时间t(0-1之间),我们找到t时的点的位置就可以了.

因此我们从画一条曲线转变为了找一个点(时间t时的点在曲线位置).

根据时间找某个时间点上 曲线上面对应的点.

那么如何找这个点呢?

我们可以看到三个点生成了两个线段b0b1,b1b2.

在b0b1线段上,我们认为下方的0是在b0处,1是在b1处,然后在b0b1上找t的对应位置,比如图中的t大约占了1/3,于是找b0 b1上的1/3处,

同理,在b1b2上,b1为0,b2为1,在b1b2也找1/3处,从而我们得到了两个新的点,接下来我们将这两个点连接起来形成一条新线段:

我们依旧认为b0b1上的新点对应0,b1b2上的新店对应1,在这条新线段上找t,也就是在找1/3处.此时找出的这个点就是时间t时曲线上的点.

我们说过显式表示要么是直接定义,要么是通过参数,t显然是一个参数,因此贝塞尔曲线是显式表示.

因此,任意一个时间t我们都可以通过这种做法做到其在曲线上的点,那么画出曲线我们只需要枚举出所有的可能性,自然就形成了一条曲线.

因此不论是几个控制点,我们都可以运用这个类似递归的算法去求出时间t时曲线的点的位置.

假设有n个控制点:

1)在每两个点之间找到t的位置,从而找到 (原先点的个数 – 1) 个新的点

2)每两个新的点连接形成新线段

3)重复前两步的操作,当得到新的点数量为1时停止,最后得到的这个点就是在t时曲线上的点.

那么将控制点的位置和时间t放在一起一定会有一个代数的表示方法,来表示时间t时,曲线的点的位置:

我们输入了四个点,每两个点之间找它的t处,就相当于在他们两个之间作了一个位置的线性插值,也就是

** (1 - t) X b0 + t X b1 **

因为t=0时,新求出的点的位置应该在b0处,t=1时应该在b1处,老师的图上标反了.
从而我们得出了这个点.

接下来都按照这个操作来进行,直到我们求出最后一个点.我们可以显式的将其表达出来:

最后一个点我们可以将其展开为:

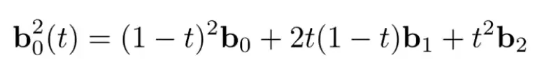
我们可以看出,这个式子中的多项式系数其实就是(s + t) ^ 2的多项式系数,只是将s代表了(1-t).

我们可以得到一个结论,给定了n+1个控制点,从0,1,2,3…n,可以得到一个n阶的贝塞尔曲线,这个贝塞尔曲线在任意时间t都是之前给定的这些控制点的线性组合,组合的系数就是一个和时间t有关的多项式::

这个多项式叫做伯恩斯坦多项式.

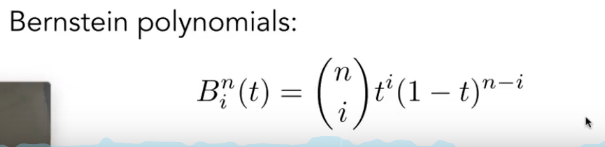
或者可以这么理解:

我们把规则总结一下:
任意阶数的贝塞尔曲线在时间t时的位置是由伯恩斯坦多项式作为系数对给定的控制点的加权.

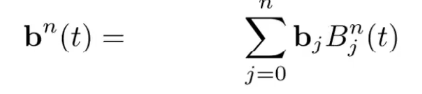
通过这么一个推导我们可以得到一些不错的性质比如例子中的各个控制点是在三维空间的点,也就是控制点不只存在于平面上,空间内也可以,我们只需要把控制点的坐标输入成三维的就可以了:

贝塞尔曲线规定了

b(0) = b0(起点),切线为3(b1 - b0)

,b(1) = b1(终点),切线为3(b3 - b2)
这里的这个系数3是由控制点决定的,n个控制点时系数为(n-1).

好了至此就是贝塞尔曲线原理的所有内容了，最后我们对贝塞尔曲线的几点性质做一个概括:

• 1 必定经过起始与终止控制点

• 2 必定经与起始与终止线段相切

• ** 3 具有仿射变换性质，可以通过移动控制点移动整条曲线**

• 4 凸包性质，曲线一定不会超出所有控制点构成的多边形范围

凸包::

Piecewise Bezier Curve(逐段贝塞尔曲线)

对于这种控制点很多的贝塞尔曲线,由于控制点众多，很难控制局部的贝塞尔曲线形状，如上图的曲线过于平滑.

因此为了解决该问题，有人提出了分段贝塞尔曲线，即将一条高次曲线分成多条低次曲线的拼接，我们一般用每四个控制点来定义一段逐段的曲线,也就是习惯使用三次贝塞尔曲线(四个控制点)当作分段曲线,如下图:

在物理上这些曲线是连续的,但是如果想要使得拼接的点看起来较为光滑不那么突兀的话，就要满足一些连续条件如一阶连续(连接点导数的左右极限相等)，二阶连续等等

第一段曲线的终点 = 第二段曲线的起点时,

我们称其为C0连续.

切线连续,也就是第一段终点的切线方向与第二段起点的切线方向共线距离相同,我们称其为C1连续,也叫做切线连续.

贝塞尔曲面

其实在理解了贝塞尔曲线之后，贝塞尔曲面的原理也是十分容易理解的了，无非是一个从2维到3维的过渡。

• 1 我们在平面上定义4 X 4个控制点,也就是认为他有4行.
  
• 2 每一行,我们拿出四个控制点来画一条三次贝塞尔曲线,从而得到了四条三次贝塞尔曲线,也就是蓝线.

• 3 四条曲线上的蓝点在不同的时间 u 上的位置也不一样.
  

• 4我们以时间u时,四个蓝点为控制点,在做一条三次贝塞尔曲线,并且也有一个时间 v ,从而我们得到了列方向上的贝塞尔曲线.

• 5 我们遍历u和v就可以求出一个贝塞尔曲面.
• 
  到此贝塞尔曲线和贝塞尔曲面就讲解完毕了,下节课我们会来学习以下曲面细分和曲面简化.