林轩田《机器学习基石》（五）—— Training versus Testing

最新推荐文章于 2024-07-06 22:59:16 发布

不抱我起来就没法医治

最新推荐文章于 2024-07-06 22:59:16 发布

阅读量160

点赞数

分类专栏：机器学习基石文章标签：机器学习

本文链接：https://blog.csdn.net/weixin_43463276/article/details/107370101

版权

机器学习基石专栏收录该内容

16 篇文章 4 订阅

订阅专栏

这节课的主要内容依旧是机器学习的可行性。

一、之前问题回顾与现在新问题的思路

上一节课回顾：在有些时候机器学习似乎是不可行的，但是如果添加了约束：如果样本数据足够大，且hypothesis个数有限，那么机器学习一般就是可行的。

进一步提问，如果当hypothesis的个数是无限多的时候，机器学习的可行性是否仍然成立？

现在具体讲一下之前几节课的架构：

以下是学习的流程图

已知一个批处理有监督的问题， $g \approx f \Longleftrightarrow E_{\text {out }}(g) \approx 0$ 。

机器学习的主要目标分成两个核心的问题（如果满足以下两点我们就可以说达到了学习的效果）：

1.在上一章讲过的，在一些约束之下，以下式子是成立的。

2.在第二节课讲过的，使用PLA等方法可以使得如下式子成立。

那么我们来讨论hypothesis set的个数M对上面两个结果的影响。

由式子

$P\left[\left|E_{i n}(g)-E_{o u t}(g)\right|>\epsilon\right] \leq 2 \cdot M \cdot \exp \left(-2 \epsilon^{2} N\right)$

M较小：依据公式，1成立；但是由于算法A的选择太少，从而不一定能找到使2足够小的h，所以2不成立。

M较大：依据公式，1不成立；由于算法A现在有足够多的选择，所以2成立。

所以M的选择对机器学习是有影响的，而且M不能太大也不能太小。那么如果M无限大的时候，肯定是有负面影响的，那机器就不能学习了吗？

思路：如果我们能用一个有限的 $m_H$ 去代替无限的M就好了。

二、有效直线

首先，我们先来阐述一下为什么有公式了，我们还要讨论M是不是还可以缩小。

因为在计算

$P\left[\left|E_{i n}(g)-E_{o u t}(g)\right|>\epsilon\right] \leq 2 \cdot M \cdot \exp \left(-2 \epsilon^{2} N\right)$

我们使用了联级不等式：

$\mathbb{P}\left[\mathcal{B}_{1} \text { or } \mathcal{B}_{2} \text { or }\leq \ldots \mathcal{B}_{M}\right] \leq \mathbb{P}\left[\mathcal{B}_{1}\right]+\mathbb{P}\left[\mathcal{B}_{2}\right]+\ldots+\mathbb{P}\left[\mathcal{B}_{M}\right]$

这个将后面的缩放的太大了，实际上这些P（B）还是有交集的（像下图），所以其实右边被放得很大，换句话说M实际上没那么大。

那么我们如何找到这些交集呢？

我们可以对h进行分类，然后我们或许可以知道哪些部分有重叠。

如何对h进行分类：

举一个简单例子。

对于二维平面中的一个点，h只会有两类，一种是把x分为负类的h，一种是分类为正类的。

如果平面上有两个点 $x_1, x_2$ ，那么直线的种类共4种：

那么对于三个点呢？

答案是八种，但是对于三个点位于同一直线这种特殊情况，答案是少于8种的。

对于四个点：

出现了用一条线没有办法划分的情况（正负调换各算一种），所以一共是2^4-1*2=14种

综上，

有效直线的数量总是满足 $\leq 2^N$ ，因此我们可以用含N的式子，替换之前公式中的M

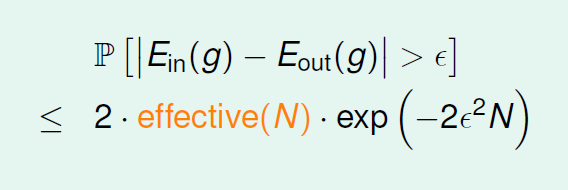
如果 $effective(N) <<2^{N}$ ，那么我们可以得到不等式右边接近于零，那么即使M无限大，直线的种类也很有限，机器学习也是可能的。

三、成长函数

二分类（dichotomy）就是将空间中的点分成正类（蓝色o）和负类（红色x）。令H是将平面上的点用直线分开的所有hypothesis h的集合，给出hypotheses H和N个点，我们究竟可以做出多少种dichotomy呢？

我们先定义符号：我们将dichotomy放入到一个集合中，

比较hypotheses set和dichotomy的区别：

hypotheses H在平面上对输入空间X里所有的点来取值，是所有直线的集合，个数可能是无限个，而dichotomy只针对N个x进行取值，是平面上能将点完全用直线分开的直线种类，它的上界是2^N。

我们能不能用dichotomy的大小来代替原来的M？

有一个小麻烦：我们的dichotomy取决于已知的资料 $x_1, x_2,...,x_n$ 。所以我们想要移除dichotomy对资料的依赖。解决方法：我们可以看看最多可以有多少种类的h，即dichotomy的最大个数，换算成数学表达就是：

这个最大的值，就称为成长函数。可以看到，成长函数与N有关，它是有限的，上界是2^N。

下面看几个例子的成长函数，先看一维的情况;

相当于对一维数轴的N个点进行分类，

如图，只有阈值的的正方向被分类为正。

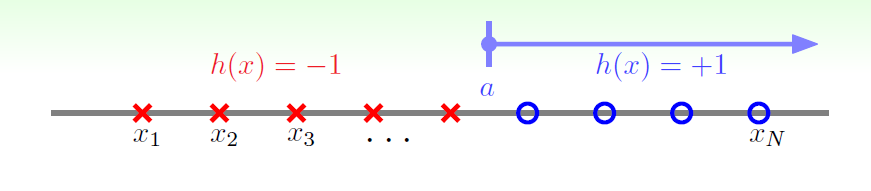
h可以被写成（a取任意实数，所以hypotheses H有无限个h，但是不知道dichotomy H有多少）：

$h(x)=\operatorname{sign}(x-a)$

可以看出分类正负由阈值a决定，一共有N+1种h。

换另一种构建h的方式：

$h(x)=+1\quad if \quad x \in[\ell, r), -1 \quad otherwise$

可以看出，h可以看做一个区间，只有在区间内才被分类为正。

所以成长函数为：

再来看二维情况：

h的构建如下所示：

相当于h是一个凸集，当在凸集内时，点被分类为正。

由于成长函数是dichotomy的最大个数。所以我们看如何分布数据才有可能找到dichotomy的最大个数，为了使得点两两间不受影响，所以我们使得数据集D按照如下的凸分布，即所有的数据点围成一个圆圈。

给出它的成长函数：

$m_H =2^N$ 。这种情况下，N个点所有可能的分类情况都能够被hypotheses set覆盖，我们把这种情形称为shattered。

四、有“希望”的点：break point

回顾上述四种成长函数

我们回到最先提出的那个问题：我们能不能用dichotomy的大小（或者直接说是用成长函数）来代替原来的M？

可以看到，当 $m_H(N)$ 是多项式，那么不等式右端的表现会很好，很接近0，但如果是指数式，那么效果就会不好。

对于2D perceptrons，

1个点：2^1

2个点：2^2

3个点：2^3

这些一直都是按指数增长的，这是坏情况。但是在下一个点，我们可能会看到一丝丝希望。它打破了指数式。

而4个点，就无法做出所有16个点的dichotomy了。所以，我们就把4称为2D perceptrons的break point（5、6、7等都是break point）。显然，我们有兴趣的是第一个break point。下面给出数学说明：

给出上面四种情况的break point:

O(N)等是成长速度，计算方式为：

（具体证明方式以后会讲）

总结：

不抱我起来就没法医治

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
林轩田《机器学习基石》（五）—— Training versus Testing

这节课的主要内容依旧是机器学习的可行性。一、之前问题回顾与现在新问题的思路上一节课回顾：在有些时候机器学习似乎是不可行的，但是如果添加了约束：如果样本数据足够大，且hypothesis个数有限，那么机器学习一般就是可行的。进一步提问，如果当hypothesis的个数是无限多的时候，机器学习的可行性是否仍然成立？现在具体讲一下之前几节课的架构：以下是学习的流程图已知一个批处理有监督的问题，。机器学习的主要目标分成两个核心的问题（如果满足以下两点我们就可以说达到了学习的效果）：
复制链接

扫一扫