上次介绍了线性回归问题,用平方误差计算出w。本节课介绍Logistic regression:逻辑斯蒂回归。
一、Logistic regression问题
学习流程图,比如我们要看病人是否有心脏病,
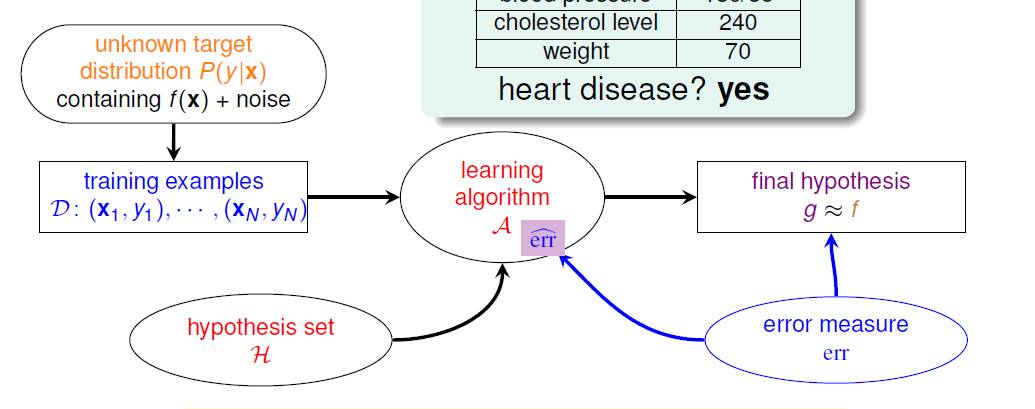
左上角说我们拿到的资料可能有noise,x是病人特征,这个目标分布P会对应一个理想的目标函数f,
当我们想知道病人有没有心脏病,做二分类问题:
![]()
今天一个类似的问题,我们不想知道他有没有心脏病,我们想知道病人心脏病的可能性是多少?我们想要得到一个[0,1]之间的值P(y|x),我们的目标函数f就变为
![]()
这个值越接近1,表示正类的可能性越大;越接近0,表示负类的可能性越大。
所以,比如在病人问题中,我们希望的资料是label y是病人患病的可能性,如,

但是实际中我们并不能拿到这样的label,医院里的病人只知道病人的病历(是否心脏病发),所以实际我们不知道具体的概率数字是多少。

我们可以把手上的的资料看做上面理想资料的有noise版本:

比如第一行 的label:0.9(真实)+0.1(noise)=1(我们实际拥有的)
我们现在要讨论的问题是:我们手上的资料是原来二分类问题的资料,现在想得到的目标函数f的输出是一个0~1之间的值,那么我们如何选择h?
根据我们之前的做法,对病人x所有的特征值进行加权处理,计算出一个分数。
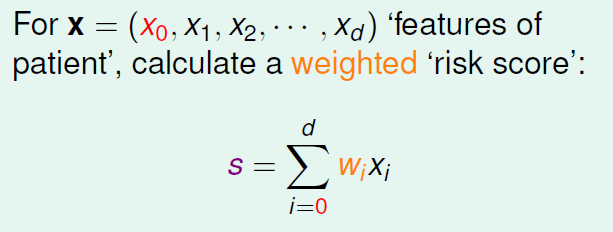
此刻分数并不是我们首要在乎的,想得到的目标函数f的输出是一个0~1之间的值。如何将前者“分数”转化为后者呢?
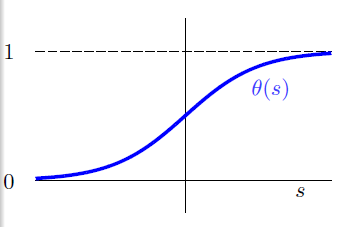
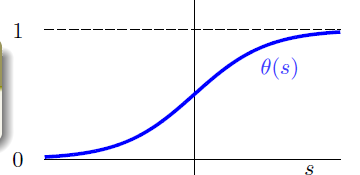
横轴是分数s,纵轴是0-1之间的数字,这样任何的分数s都可以转化为[0,1]之间。我们把这个转化函数叫做Logistic函数,记作。
Logistic函数公式
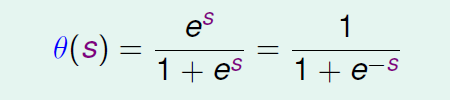
这个公式希望当分数越高时候,输出越靠近1,分数越低,输出越靠近0.
我们学习到的h就是:
![]()
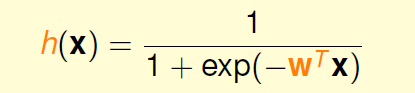
二、Logistic回归误差
线性分类问题使用了:
1.线性scoring function
2.h = sign(s)
3.0-1误差
线性回归问题使用了:
1.线性scoring function
2.h = s,不需要使用函数 sign(x)
3.平方误差
Logistic回归:
1.线性scoring function
2.h =
3.???
所以,现在到的问题是Logistic回归的err长什么样?
首先声明,我们的目标函数f是(也可以选择是P(-1|x),那么下面的P(y|x)也随之稍作改动):
![]()
有
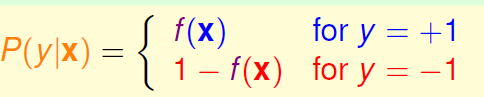
同理先已知P(y|x)再推上面的f(x)也是成立的。
我们假设x独立同分布(iid),那么若给了f,产生资料D的概率为:
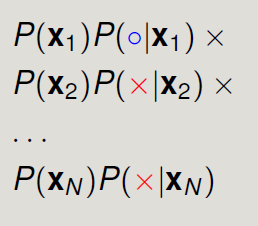 →
→ 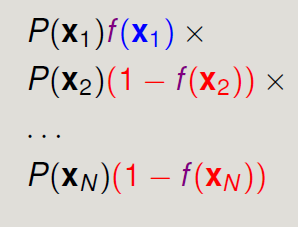
现在我们假装h就是我们要找的f,那么

如果今天h和f很接近,那么h产生这个资料的可能性与f产生这个资料的可能性是几乎一样的(他们之间“可能性”的差别就是err)。现在本来就是假设f是这些资料的目标函数,那么换句话说,f产生了这些资料(概率说法是:f产生这个资料的可能性非常非常大)。既然这样,我们也要h产生这个资料的可能性非常非常大。所以我们想要找到使得上述概率最大的h来当做要找的g。

Logistic函数特性
![]()
极大似然函数为,灰色部分是每个h都一样的部分,所以只需要看其他有颜色的部分即可
![]()
我们要找的就是使得似然函数最大的h

由于我们考虑的是线性加权的h,所以h由权重w决定,因此可以变为:
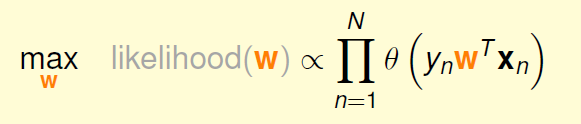
我们进一步希望连乘变为连加的形式,所以取ln:
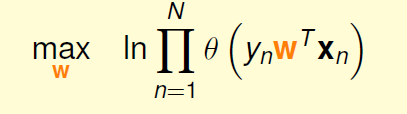
ln放入连乘变为连加,之后进一步把最大化改写为最小化:
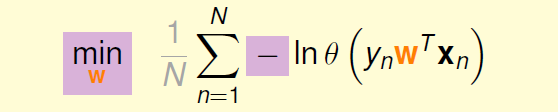
我们将
![]()
代入上式:
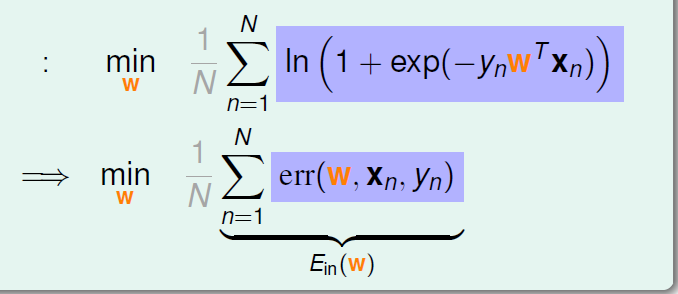
紫色的部分是Logistic回归的err,称为cross-entropy error交叉熵误差。
![]()
三、Logistic回归误差的梯度
接下来的问题就是如何找到合适的向量w,让上述的最小。
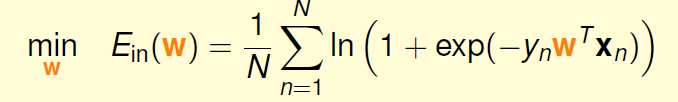
我们先给出的图像与性质:
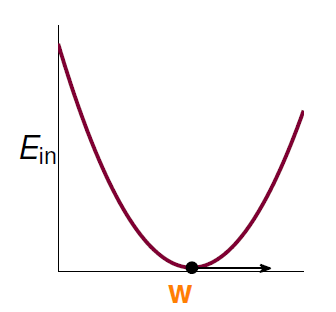
性质:连续,可微,二次可微,凸。
我们要找到极小值,也就是要找w使其满足
![]()
现在我们来求的梯度,我们先做一些记号,这样比较好求:
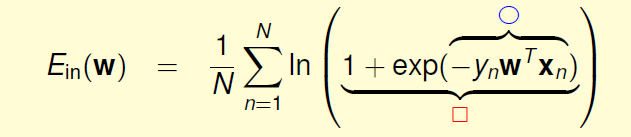
过程:
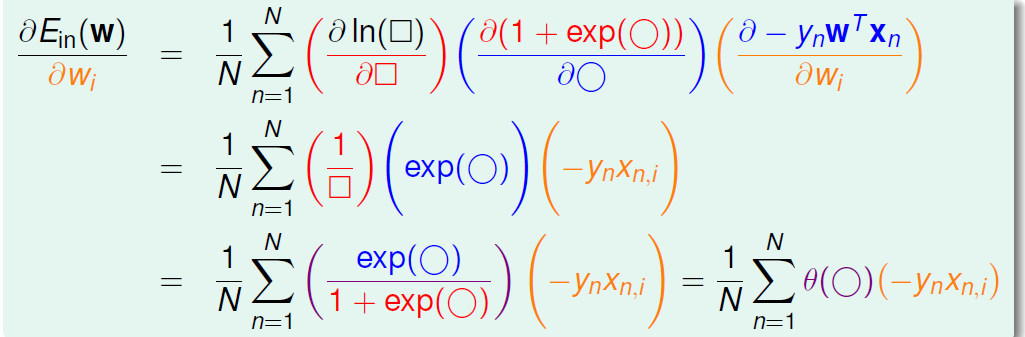
上面是每一个的梯度,把他们整合起来结果是(用向量方式来简洁表达):
![]()
为了计算最小值,我们就要找到让
的梯度等于0的位置。
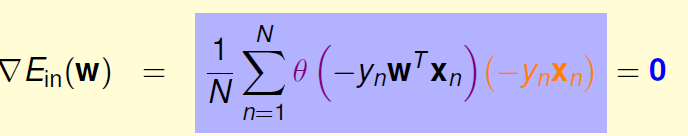
有一种可能性:可以看到只要让![]() ,那么最终结果就会等于0.
,那么最终结果就会等于0.图像为
当的时候,
可能为0,即
——这代表每一个资料都可以被分类正确,也就是资料是线性可分的。
但现在如果不是线性可分,那么要研究如何求解w,用式子直接解的话,显然是没有闭式解的。
之前所说的Linear Regression有closed-form解,可以说是“一步登天”的。PLA算法是一步一步修正迭代进行的,每次对错误点进行修正,不断更新w值。PLA的迭代优化过程表示如下:
即找到一个分类错误的点,用它去修正w

最后一步的w作为我们要找的g的权重。
把上面两步再简化一下,得到一步:

仔细的分析一下上面更新w的式子:
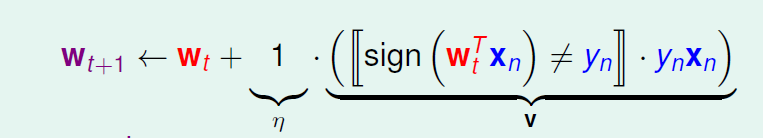
v表示更新的方向,可以发现我们加了一个常数‘1’进来,作为步长(每次朝方向上走多少)。参数(v,η)和终止条件决定了迭代优化算法。
四、梯度下降法
我们现在的任务就是找:v和η。PLA中v来自错误修正。
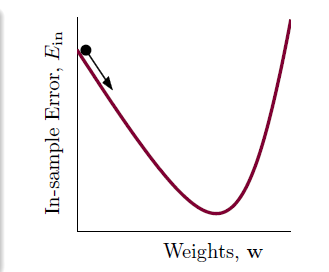
我们把曲线看做是一个山谷的话,要求
最小,可以看做是小球到山底的过程。
在整个下山过程的两个重要因素为:
1.方向v,通常看做是单位长度的
2.下山的步长η,通常是正的。
一个贪心的方法,我想快点走向山底,所以η如果给定,那么我们选择的方向就是最陡的方向:
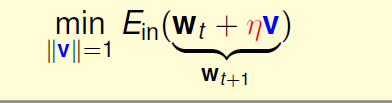
上述的优化问题没有使得实际变得好求解(甚至加了一些方向上的约束等),我们期待它转变为更容易的问题(比如一些线性的问题):
我们可以做泰勒展开
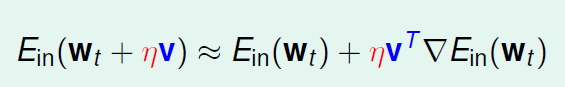
上面的问题随之变为一个线性的问题:

(灰色的其实对优化问题没有影响,因为那就是固定值,所以除去灰色部分就是我们最终的优化问题)
我们可以看到什么样的v是最好的,当v和是反方向时候(由于两个向量乘积是两个模乘积×夹角余弦,
已知,v的模要求是1,所以夹角余弦值最小为-1,即相反方向),取得最小值。除以
是为了让v的模为1.
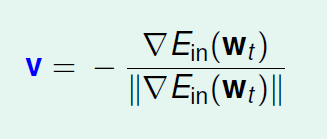
所以梯度下降法是:朝着v移动一小步η,
![]()
如何选择步长η
步长太小会导致走的很慢:
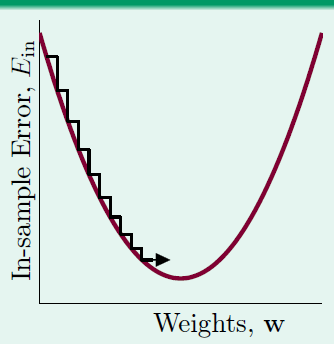
步长太大会导致走的不稳定:
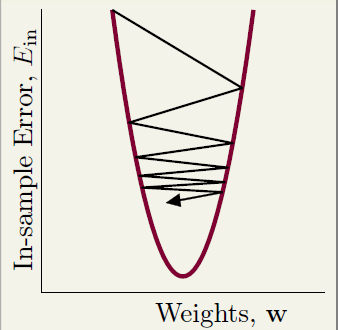
适中的步伐好,或者使用动态的步长,在陡的时候走的步子大,在稍微平缓时候走的步子小:
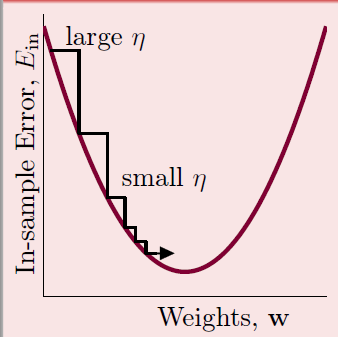
坡度最直观的判断是,当
大时候坡度大,当
小的时候坡度小。所以希望η在
大的时候大,在
小的时候小,即η正比于
,我们把这个比例作为新的η,这样他就是固定的了,这个固定比率叫做学习率η。迭代公式也变为:
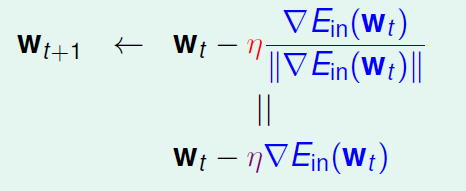
综上,算法如下所示:

初始化→计算梯度→更新 重读计算更新后的梯度 直到梯度约为0或者跑了足够多的步长.
总结























 159
159











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








