图论

图的存法

• 邻接矩阵
  邻接矩阵是使用一个二维数组存储图，他的特点是，好打，好理解。but，占内存看起来没有邻接表高级
• 邻接表
  邻接表通常常用的有两种，一种是用vecter模拟（咳咳，这不是边集数组差不多嘛），另外一种是链式前向星，链式前向星是一种数组模拟指针的存图方式
  他是长这个样子的：

struct edge {
     int next; //上一个儿子的地址
     int to;  //儿子
     int w;  //根据题意，存储其他信息，比如权值，也可没有
} e[N<<1] //通常存有向图，开边数的两倍
int h[N<<1];//最小的儿子的地址
int cnt; //地址
// 这里的地址不是指针所指向的那个地址，而是cnt++的过程中不断地给，每个边附上的地址。。emm。。编码

然后存图

void add(int u,int v) {
	e[++cnt].to=v;
	e[cnt].next=h[u];//上个儿子地址
	h[u]=cnt; //更新最新的儿子
}

链式前向星存图中，最小的儿子是最后存入的，所以他的遍历是后序遍历，代码：

for(int i=h[u],v;v=e[i].to,i;i=e[i].next)

最短路算法

emmm…手动跳转一下—>最短路啦

最小生成树

说到图，怎么能不说一下树呢（QAQ）
最小生成树是在一个给定的无向图G（V,E）中求一棵树T，使得这棵树拥有图G中的所有顶点，且所有边都是来自图G中的边，并且满足整棵树的边权之和最小

【性质】

最小生成树是树，因此其边数等于顶点数减1，且树中一定不会有环
对给定的图G但其（V,E），其最小生成树可以不唯一，但其边权之和一定是唯一的
由于最小生成树是在无向图上生成的，因此其根结点可以是这棵树上的任何一个结点
一般求解最小生成树有两种算法
即prim算法和kruskal算法
（都采用了贪心算法）

prim
弱弱的表示prim比kruskal难多了
基本思想是对图G（V,E）设置集合S，存放已被访问的顶点然后每次从集合V-S中选择与集合S的最短距离最小的一个顶点（记为u访问并加入集合S之后，令顶点u为中介点优化所有从u能到达的顶点v与集合S之间的最短距离这样的操作执行n次（n为顶点个数）直到集合S已包含所有顶点
说的好累。。。其实就是和迪杰斯特拉的思想差不多了
kruskal
kruskal相对简单多了
整个的代码实现就是。。。。先按照权值从小到大sort一遍，然后能取就取（能取就是指加入之后不会产生环），整个的就是一个贪心的思想，我们可以用并查集来实现

int find(int x) {return f[x]==x?x:f[x]=find(f[x]);}

void kruskal(){
	for(int i=1;cnt!=n-1;++i){
		int r1=find(edge[i].start),r2=find(edge[i].end);
		if(r1!=r2) {
			f[find(r1)]=find(r2),cnt++;
			if(edge[i].c==0) temp++;
			    ans+=edge[i].v;
		}
	}
}

其实可以跳转一道用克鲁斯卡尔解的题目—>
宣传博客咳咳

次小生成树

结束了最小生成树，来毒一下最小生成树
次小生成树的定义
设 G=(V,E,w)是连通的无向图，T 是图G 的一个最小生成树。如果有另一棵树T1，满
足不存在树T’,ω（T’）<ω（T1） ，则称T1是图G的次小生成树。

求解次小生成树的算法
约定：

由T 进行一次可行交换得到的新的生成树所组成的集合，称为树T的邻集,记为N(T)。 定理
3：设T是图G的最小生成树，如果T1满足ω(T1)=min{ω(T’)| T’∈N(T)},则T1是G 的次小生成树。

证明：如果 T1 不是G 的次小生成树，那么必定存在另一个生成树T’,T’=T 使得
ω(T)≤ω(T’)<ω(T1)，由T1的定义式知T不属于N(T)，则E(T’)/E(T)={a1,a21,……,at}，E(T)/E(T’)={b1,b2,……,bt}，其中t≥2。根据引理1 知，存在一个排列bi1,bi2,……,bit，使得T+aj-bij仍然是G 的生成树，且均属于N(T),所以ω(aj)≥ω(bij)，所以ω(T’)≥ω(T+aj-bij)≥ω(T1)，故矛盾。所以T1是图G 的次小生成树。通过上述定理，我们就有了解决次小生成树问题的基本思路。
首先先求该图的最小生成树T。时间复杂度O(Vlog₂V+E)然后，求T的邻集中权值和最小的生成树，即图G 的次小生成树。如果只是简单的枚举，复杂度很高。首先枚举两条边的复杂度是O(VE)，再判断该交换是否可行的复杂度是O(V)，则总的时间复杂度是O(V2E)。这样的算法显得很盲目。经过简单的分析不难发现，每加入一条不在树上的边，总能形成一个环，只有删去环上的一条边，才能保证交换后仍然是生成树，而删去边的权值越大，新得到的生成树的权值和越小。我们可以以此将复杂度降为O(VE)。这已经前进了一大步，但仍不够好。
回顾上一个模型——最小度限制生成树，我们也曾面临过类似的问题，并且最终采用动态规
划的方法避免了重复计算，使得复杂度大大降低。对于本题，我们可以采用类似的思想。首
先做一步预处理，求出树上每两个结点之间的路径上的权值最大的边，然后，枚举图中不在
树上的边，有了刚才的预处理，我们就可以用O(1)的时间得到形成的环上的权值最大的边。
如何预处理呢？因为这是一棵树，所以并不需要什么高深的算法，只要简单的BFS 即可。
预处理所要的时间复杂度为O(V²)。这样，这一步时间复杂度降为O(V²)。综上所述，次小生成树的时间复杂度为O(V²)。

结论1
次小生成树可由最小生成树换一条边得到.

证明:
可以证明下面一个强一些的结论：
T是某一棵最小生成树，T0是任一棵异于T的树，通过变换T0 --> T1 --> T2 --> … --> Tn (T) 变成最小生成树.所谓的变换是，每次把Ti中的某条边换成T中的一条边, 而且树T(i+1)的权小于等于Ti的权.
具体操作是：
设max[i,j]表示在最小生成树中任意两个点i，j的唯一路径中
特别地：取T0为任一棵次小生成树，T(n-1) 也就是次小生成树且跟T差一条边. 结论1得证.
代码：

二分图匹配

说到二分图，首先看一下二分图是什么

二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j B)，则称图G为一个二分图。
简单的说（上面都是废话），一个图被分成了两部分，相同的部分没有边相连，那这个图就是二分图。

匹配
二分图的匹配通常是用匈牙利算法
注：以下转自 http://blog.csdn.net/dark_scope/article/details/8880547

匈牙利算法是由匈牙利数学家Edmonds于1965年提出，因而得名。匈牙利算法是基于Hall定理中充分性证明的思想，它是部图匹配最常见的算法，该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法。

-------等等，看得头大？那么请看下面的版本：

通过数代人的努力，你终于赶上了剩男剩女的大潮，假设你是一位光荣的新世纪媒人，在你的手上有N个剩男，M个剩女，每个人都可能对多名异性有好感（惊讶-_-||暂时不考虑特殊的性取向），如果一对男女互有好感，那么你就可以把这一对撮合在一起，现在让我们无视掉所有的单相思（好忧伤的感觉快哭了），你拥有的大概就是下面这样一张关系图，每一条连线都表示互有好感。

本着救人一命，胜造七级浮屠的原则，你想要尽可能地撮合更多的情侣，匈牙利算法的工作模式会教你这样做：

一： 先试着给1号男生找妹子，发现第一个和他相连的1号女生还名花无主，got it，连上一条蓝线

二：接着给2号男生找妹子，发现第一个和他相连的2号女生名花无主，got it

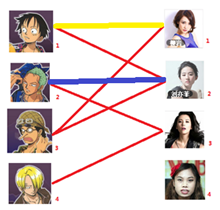
三：接下来是3号男生，很遗憾1号女生已经有主了，怎么办呢？

我们试着给之前1号女生匹配的男生（也就是1号男生）另外分配一个妹子。
(黄色表示这条边被临时拆掉)
与1号男生相连的第二个女生是2号女生，但是2号女生也有主了，怎么办呢？我们再试着给2号女生的原配(发火发火)重新找个妹子(注意这个步骤和上面是一样的，这是一个递归的过程)
此时发现2号男生还能找到3号女生，那么之前的问题迎刃而解了，回溯回去
2号男生可以找3号妹子~~~ 1号男生可以找2号妹子了~~~ 3号男生可以找1号妹子
四： 接下来是4号男生，很遗憾，按照第三步的节奏我们没法给4号男生腾出来一个妹子，我们实在是无能为力了……香吉士同学走好。
这就是匈牙利算法的流程，其中找妹子是个递归的过程，最最关键的字就是“腾”字
其原则大概是： 有机会上，没机会创造机会也要上

然后二分图匹配的代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N=1000;
int a[N][N],a[N],bb[N],vis[N],book[N][N];

int hun(int u) {
	FOR(i,1,n) if(a[u][i]&&!vis[i]) {
		vis[i]=1;
		if(!bb[i]||hun(i)){
			aa[u]=i;
			bb[i]=u;
			return 1;
		}
	}
	return 0;
}

int main() {
	FOR(i,1,n) scanf("%d%d",&x,&y),a[x][y]=a[y][x]=1;
	FOR(i,1,n) {
		FOR(i,1,n) vis[i]=0;
		if(!aa[i]) sum+=hun(i);
	}	
	return 0;
}

LCA

LCA的做法非常的多，有在线的，有离线的，这里，首先讲一下倍增求LCA

倍增求LCA的思路是：

1. 首先运用dfs，处理出每个节点的深度
2. 预处理出每个节点的祖宗们（突然皮）
3. 每次求lca时，如果深度不同，先跳到同一深度，然后一起向上跳，直到相遇（这一过程中，为了加速，使用了倍增的思想）

代码如下：

#include<bits/stdc++.h>
#define FOR(i,n,m) for(int i=n;i<=m;++i)
#define FR(i,n,m) for(int i=n;i>=m,--i)
using namespace std;
struct EDGE {int next;int v;} a[1000001];
int head[500001],cnt=0,n,m,root,d[500001],f[500001][21];
void add(int x,int y) {
	cnt++;a[cnt].v=y;
	a[cnt].next=head[x];
	head[x]=cnt;
}
inline void input() {
	scanf("%d%d%d",&n,&m,&root);
	int x,y;
	for (int i=1; i<=n-1; i++) {
		scanf("%d%d",&x,&y);
		add(x,y),add(y,x);
	}
}
void init(int son,int father) {
	d[son]=d[father]+1;
	f[son][0]=father;
	for (int i=1; (1<<i)<=d[son]; i++)
		f[son][i]=f[f[son][i-1]][i-1];
	for (int i=head[son]; i; i=a[i].next) {
		if (a[i].v!=father)
			init(a[i].v,son);
	}
}

int lca(int x,int y) {
	if (d[x]>d[y]) swap(x,y);
	FR (i,20,0) { 
		if (d[x]+(1<<i)<=d[y]) y=f[y][i];
		if (d[x]==d[y])break;
	}
	if (x==y) return x;
	FR (i,20,0) {
		if (f[x][i]==f[y][i])continue;
		else x=f[x][i],y=f[y][i];
	}
	return f[x][0];
}

int main() {
	input();d[0]=0;	init(root,0);
	int x,y;
	FOR(i,1,m) {
		scanf("%d%d",&x,&y);
		printf("%d\n",lca(x,y));
	}
	return 0;
}