【转载】JoSE:球面上的词向量和句向量
本文转载自科学空间 Blog:
苏剑林. (Nov. 11, 2019). 《JoSE:球面上的词向量和句向量 》[Blog post].
这篇文章介绍一个发表在NeurIPS 2019的做词向量和句向量的模型JoSE(Joint Spherical Embedding),论文名字是《Spherical Text Embedding》。JoSE模型思想上和方法上传承自Doc2Vec,评测结果更加漂亮,但写作有点故弄玄虚之感。不过笔者决定写这篇文章,是因为觉得里边的某些分析过程有点意思,可能会对一般的优化问题都有些参考价值。
优化目标
在思想上,这篇文章基本上跟Doc2Vec是一致的:为了训练句向量,把句子用一个id表示,然后把它也当作一个词,跟句内所有的词都共现,最后训练一个Skip Gram模型,训练的方式都是基于负采样的。跟Doc2Vec不一样的是,JoSE将全体向量的模长都归一化了(也就是只考虑单位球面上的向量),然后训练目标没有用交叉熵,而是用hinge loss:
max ( 0 , m − cos ( u , v ) − cos ( u , d ) + cos ( u ′ , v ) + cos ( u ′ , d ) ( 1 ) \max(0, m - \cos(\boldsymbol{u}, \boldsymbol{v}) - \cos(\boldsymbol{u}, \boldsymbol{d}) + \cos(\boldsymbol{u}', \boldsymbol{v}) + \cos(\boldsymbol{u}', \boldsymbol{d})\quad(1) max(0,m−cos(u,v)−cos(u,d)+cos(u′,v)+cos(u′,d)(1)
其中 u u u是“中心词”的词向量, v v v是“上下文词”的词向量,它们分别来自两套词向量空间, d d d则是当前句的句向量,而 u ′ u^\prime u′负采样得到的“中心词”词向量,最后的 m m m是一个常数。以前做相似度模型的读者应该能很轻松读懂这个优化目标的含义,它就是希望句子内的“词-词-句”打分 cos ( u , v ) + cos ( u , d ) \cos(u,v)+\cos(u,d) cos(u,v)+cos(u,d)要高于“词-随机词-句”打分 cos ( u ′ , v ) + cos ( u ′ , d ) \cos(u′,v)+\cos(u′,d) cos(u′,v)+cos(u′,d),但不需要太高,只要高出 m m m就行了。
假定 u , v , d u,v,d u,v,d都已经归一化的情况下,那么目标(1)就是(每个向量被假设为列向):
max ( 0 , m − v ⊤ u − d ⊤ u + v ⊤ u ′ + d ⊤ u ′ ) ( 2 ) \max(0, m - \boldsymbol{v}^{\top}\boldsymbol{u} - \boldsymbol{d}^{\top}\boldsymbol{u} + \boldsymbol{v}^{\top} \boldsymbol{u}' + \boldsymbol{d}^{\top} \boldsymbol{u}')\quad(2) max(0,m−v⊤u−d⊤u+v⊤u′+d⊤u′)(2)
梯度下降
目标(1)或(2)其实并没有什么新鲜之处,跟大多数词向量的目标类似,都是用内积衡量词的相关性,只不过这里的向量归一化过,所以内积就是 cos \cos cos,至于hinge loss和交叉熵孰优孰劣,我倒觉得不会有什么太大差别。
事实上,笔者觉得文章比较有意思的是它后面对梯度的几何分析,在这里笔者用自己的话重复一下求解过程。设 x x x是全体 u , v , d u,v,d u,v,d向量中的其中一个,然后假设现在固定所有的其他向量,只优化 x x x,设总的loss为 f ( x ) f(x) f(x),那这个优化过程有两种描述方式:
arg min x , ∥ x ∥ = 1 f ( x ) 或 arg min θ f ( θ ∥ θ ∥ ) ( 3 ) \mathop{\arg\min}_{\boldsymbol{x},\,\Vert\boldsymbol{x}\Vert=1} f(\boldsymbol{x})\quad\text{或}\quad \mathop{\arg\min}_{\boldsymbol{\theta}} f\left(\frac{\boldsymbol{\theta}}{\Vert \boldsymbol{\theta}\Vert}\right) \quad(3) argminx,∥x∥=1f(x)或argminθf(∥θ∥θ)(3)
也就是说,我们可以将这个问题理解为带有约束 ∥ x ∥ = 1 ∥x∥=1 ∥x∥=1的 f ( x ) f(x) f(x)最小化问题,也可以通过设x=θ/∥θ∥x=θ/‖θ‖将它转化为无约束的 f ( θ ‖ θ ‖ ) f(\frac{θ}{‖θ‖}) f(‖θ‖θ)最小化问题。由于带约束的优化问题我们不熟悉,所以只好按照后一种方式来理解。
复杂模型不同的是,词向量算是一个比较简单的模型,所以我们最好手动求出它的梯度形式,然后编写对应函数进行梯度下降来优化,而不借助于一些自动求导工具。对于 f ( θ ∥ θ ∥ ) f(\frac{θ}{\|θ\|}) f(∥θ∥θ),我们不难求得:
∇ θ f ( θ ∥ θ ∥ ) = 1 ∥ θ ∥ ( I − x x ⊤ ) ∇ x f ( x ) ( 4 ) \nabla_{\boldsymbol{\theta}}\,f\left(\frac{\boldsymbol{\theta}}{\Vert \boldsymbol{\theta}\Vert}\right) = \frac{1}{\Vert\boldsymbol{\theta}\Vert}\left(\boldsymbol{I} - \boldsymbol{x}\boldsymbol{x}^{\top}\right)\nabla_{\boldsymbol{x}}\,f\left(\boldsymbol{x}\right) \quad(4) ∇θf(∥θ∥θ)=∥θ∥1(I−xx⊤)∇xf(x)(4)
(详细过程为 ∇ θ f ( θ ∥ θ ∥ ) = ∇ x f ( x ) ⋅ ∇ θ ( θ ∥ θ ∥ ) = ∇ x f ( x ) ⋅ I ⋅ ∥ θ ∥ − θ ∥ θ ∥ ⋅ θ ⊤ ∥ θ ∥ 2 = 1 ∥ θ ∥ ( I − x x ⊤ ) ⋅ ∇ x f ( x ) \nabla_{\boldsymbol{\theta}}\,f\left(\frac{\boldsymbol{\theta}}{\Vert \boldsymbol{\theta}\Vert}\right) =\nabla_{x}f(x)\cdot\nabla_{\theta}({\frac{\theta}{\|\theta\|}})=\nabla_{x}f(x)\cdot\frac{I\cdot\|\theta\|-\frac{\theta}{\|\theta\|}\cdot\theta^{\top}}{\|\theta\|^2}=\frac{1}{\|\theta\|}(I-xx{\top})\cdot \nabla_{x}f(x) ∇θf(∥θ∥θ)=∇xf(x)⋅∇θ(∥θ∥θ)=∇xf(x)⋅∥θ∥2I⋅∥θ∥−∥θ∥θ⋅θ⊤=∥θ∥1(I−xx⊤)⋅∇xf(x),其中 ( ∥ θ ∥ ) ′ = θ ∥ θ ∥ (\|\theta\|)^{\prime}=\frac{\theta}{\|\theta\|} (∥θ∥)′=∥θ∥θ,看作标量 ( θ 1 2 + θ 2 2 + ⋯ + θ n 2 ) ′ = θ i θ 1 2 + θ 2 2 + ⋯ + θ n 2 (\sqrt{\theta_1^2+\theta_2^2+\cdots+\theta_n^2})^{\prime}=\frac{\theta_i}{\sqrt{\theta_1^2+\theta_2^2+\cdots+\theta_n^2}} (θ12+θ22+⋯+θn2)′=θ12+θ22+⋯+θn2θi)
根据上述结果,梯度下降的迭代公式为:
θ t + 1 = θ t − η t ( I − x t x t ⊤ ) ∇ x t f ( x t ) ( 5 ) \boldsymbol{\theta}_{t+1} = \boldsymbol{\theta}_{t} - \eta_t\left(\boldsymbol{I} - \boldsymbol{x}_t\boldsymbol{x}_t^{\top}\right)\nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right) \quad(5) θt+1=θt−ηt(I−xtxt⊤)∇xtf(xt)(5)
其中 η t \eta_t ηt是当前时刻的学习率,而因 1 ‖ θ ‖ \frac{1}{‖θ‖} ‖θ‖1由于只是个标量,所以被整合到学习率中了。然后我们也可以写出:
x t + 1 = θ t + 1 ∥ θ t + 1 ∥ = θ t − η t ( I − x t x t ⊤ ) ∇ x t f ( x t ) ∥ θ t − η t ( I − x t x t ⊤ ) ∇ x t f ( x t ) ∥ = x t − η t / ∥ θ ∥ × ( I − x t x t ⊤ ) ∇ x t f ( x t ) ∥ x t − η t / ∥ θ ∥ × ( I − x t x t ⊤ ) ∇ x t f ( x t ) ∥ ( 6 ) \begin{aligned}\boldsymbol{x}_{t+1} = \frac{\boldsymbol{\theta}_{t+1}}{\Vert \boldsymbol{\theta}_{t+1}\Vert} =& \frac{\boldsymbol{\theta}_{t} - \eta_t\left(\boldsymbol{I} - \boldsymbol{x}_t\boldsymbol{x}_t^{\top}\right)\nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right)}{\left\Vert \boldsymbol{\theta}_{t} - \eta_t\left(\boldsymbol{I} - \boldsymbol{x}_t\boldsymbol{x}_t^{\top}\right)\nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right)\right\Vert}\\ =& \frac{\boldsymbol{x}_{t} - \eta_t/\Vert\boldsymbol{\theta}\Vert\times\left(\boldsymbol{I} - \boldsymbol{x}_t\boldsymbol{x}_t^{\top}\right)\nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right)}{\left\Vert \boldsymbol{x}_{t} - \eta_t/\Vert\boldsymbol{\theta}\Vert\times\left(\boldsymbol{I} - \boldsymbol{x}_t\boldsymbol{x}_t^{\top}\right)\nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right)\right\Vert} \end{aligned}\quad(6) xt+1=∥θt+1∥θt+1==∥∥θt−ηt(I−xtxt⊤)∇xtf(xt)∥∥θt−ηt(I−xtxt⊤)∇xtf(xt)∥∥xt−ηt/∥θ∥×(I−xtxt⊤)∇xtf(xt)∥∥xt−ηt/∥θ∥×(I−xtxt⊤)∇xtf(xt)(6)
再次将 1 ∥ θ ∥ \frac{1}{\|\theta\|} ∥θ∥1整合到学习率中,将得到只有 x t x_t xt的更新公式:
x t + 1 = x t − η t ( I − x t x t ⊤ ) ∇ x t f ( x t ) ∥ x t − η t ( I − x t x t ⊤ ) ∇ x t f ( x t ) ∥ ( 7 ) \boldsymbol{x}_{t+1} = \frac{\boldsymbol{x}_{t} - \eta_t\left(\boldsymbol{I} - \boldsymbol{x}_t\boldsymbol{x}_t^{\top}\right)\nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right)}{\left\Vert \boldsymbol{x}_{t} - \eta_t\left(\boldsymbol{I} - \boldsymbol{x}_t\boldsymbol{x}_t^{\top}\right)\nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right)\right\Vert}\quad(7) xt+1=∥∥xt−ηt(I−xtxt⊤)∇xtf(xt)∥∥xt−ηt(I−xtxt⊤)∇xtf(xt)(7)
更新量的修正
对下降的梯度进行如下变换,首先有:
g = ( I − x t x t ⊤ ) ∇ x t f ( x t ) = ∇ x t f ( x t ) − x t x t ⊤ ∇ x t f ( x t ) = ∇ x t f ( x t ) − x t ∥ ∇ x t f ( x t ) ∥ cos ( x t , ∇ x t f ( x t ) ) (由 ∥ x t ∥ = 1 保证) ( 8 ) \begin{aligned}\boldsymbol{g}=&\left(\boldsymbol{I} - \boldsymbol{x}_t\boldsymbol{x}_t^{\top}\right)\nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right)\\ =&\nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right) - \boldsymbol{x}_t\boldsymbol{x}_t^{\top}\nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right)\\ =&\nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right) - \boldsymbol{x}_t\Vert \nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right)\Vert \cos\left(\boldsymbol{x}_t,\nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right)\right) \text{(由}\|x_t\|=1 \text{保证)} \end{aligned} \quad(8) g===(I−xtxt⊤)∇xtf(xt)∇xtf(xt)−xtxt⊤∇xtf(xt)∇xtf(xt)−xt∥∇xtf(xt)∥cos(xt,∇xtf(xt))(由∥xt∥=1保证)(8)
可以看到, x t x t ⊤ ∇ x t f ( x t ) x_tx_t^{\top}\nabla_{x_t}f(x_t) xtxt⊤∇xtf(xt)实际上就是向量 ∇ x t f ( x t ) \nabla_{x_t}f(x_t) ∇xtf(xt) 在 在 在 x t x_t xt方向上的投影分量,而整个 g g g其实就是一个与 x t x_t xt垂直的向量,如下图示:
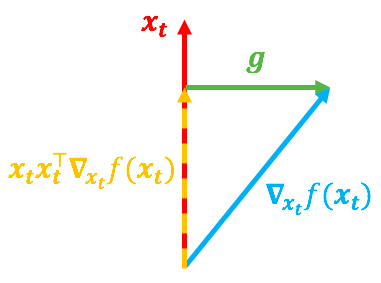
在上图中,红色向量代表 x t x_t xt,蓝色向量代表 ∇ x t f ( x t ) \nabla_{x_t}f(x_t) ∇xtf(xt),如果没有 ∥ x t ∥ = 1 \|x_t\|=1 ∥xt∥=1的约束的话,更向量将直接由 ∇ x t f ( x t ) \nabla_{x_t}f(x_t) ∇xtf(xt)决定,但是因为有了约束,所以更新量由 g = ( I − x t x t ⊤ ∇ x t f ( x t ) ) g=(I-x_tx_t^{\top}\nabla_{x_t}f(x_t)) g=(I−xtxt⊤∇xtf(xt))决定。然而,有下面两种不同的 ∇ x t f ( x t ) \nabla_{x_t}f(x_t) ∇xtf(xt),都可能导致同一个 g g g:
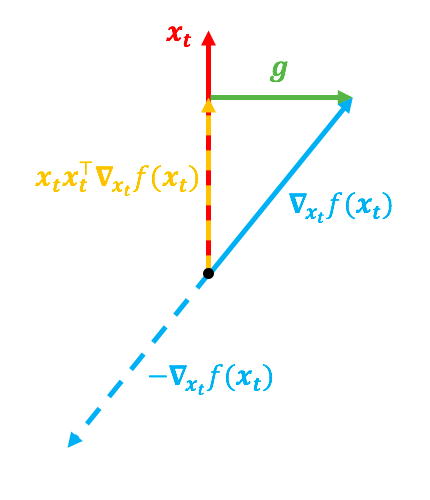
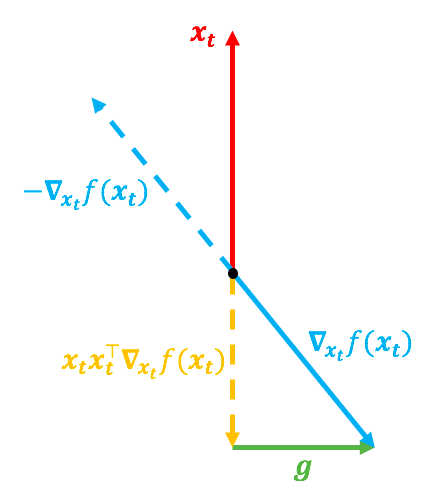
第一种情况的 ∇ x t f ( x t ) \nabla_{x_t}f(x_t) ∇xtf(xt)的方向跟 x t x_t xt很靠近,第二种情况则相反,但它们的 g g g是一致的。前面说了,如果没有约束的话, ∇ x t f ( x t ) \nabla_{x_t}f(x_t) ∇xtf(xt)才是梯度,换言之 − ∇ x t f ( x t ) -\nabla_{x_t}f(x_t) −∇xtf(xt)就是合理的更新方向;现在有了约束, − ∇ x t f ( x t ) -\nabla_{x_t}f(x_t) −∇xtf(xt)虽然不能指出最合理的梯度方向,但直觉来看,它应该还是跟更新量有关的。
在第一种情况下, − ∇ x t f ( x t ) -\nabla_{x_t}f(x_t) −∇xtf(xt)跟 x t x_t xt方向差得比较远,意味着这种情况下更新量应该大一些;而第二种情况下, − ∇ x t f ( x t ) -\nabla_{x_t}f(x_t) −∇xtf(xt)跟 x t x_t xt方向比较一致,而我们只关心 x t + 1 x_{t+1} xt+1的方向,不关心它的模长,所以按理说这种情况下更新量应该小一些。
所以,哪怕这两种情况下 g g g都一样,我们还是需要有所区分,一个很自然的想法是:既然 − ∇ x t f ( x t ) -\nabla_{x_t}f(x_t) −∇xtf(xt)和 x t x_t xt的方向的一致性会对更新量的大小有所影响,所以不妨用
1 − cos ( − ∇ x t f ( x t ) , x t ) = 1 + x t ⊤ ∇ x t f ( x t ) ∥ ∇ x t f ( x t ) ∥ ( 9 ) 1-\cos(-\nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right),\boldsymbol{x}_t)=1+\frac{\boldsymbol{x}_t^{\top}\nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right)}{\left\Vert \nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right)\right\Vert} \quad(9) 1−cos(−∇xtf(xt),xt)=1+∥∇xtf(xt)∥xt⊤∇xtf(xt)(9)
来调节更新量,这个调节因子刚好满足“方向越一致,调节因子越小”的特性。自然就形成了最终的更新公式
方向越一致,cos值越大,-cos值越小,调节因子小
x t + 1 = x t − η t ( 1 + x t ⊤ ∇ x t f ( x t ) ∥ ∇ x t f ( x t ) ∥ ) ( I − x t x t ⊤ ) ∇ x t f ( x t ) ∥ x t − η t ( 1 + x t ⊤ ∇ x t f ( x t ) ∥ ∇ x t f ( x t ) ∥ ) ( I − x t x t ⊤ ) ∇ x t f ( x t ) ∥ ( 10 ) \boldsymbol{x}_{t+1} = \frac{\boldsymbol{x}_{t} - \eta_t\left(1+\frac{\boldsymbol{x}_t^{\top}\nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right)}{\left\Vert \nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right)\right\Vert}\right)\left(\boldsymbol{I} - \boldsymbol{x}_t\boldsymbol{x}_t^{\top}\right)\nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right)}{\left\Vert \boldsymbol{x}_{t} - \eta_t\left(1+\frac{\boldsymbol{x}_t^{\top}\nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right)}{\left\Vert \nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right)\right\Vert}\right)\left(\boldsymbol{I} - \boldsymbol{x}_t\boldsymbol{x}_t^{\top}\right)\nabla_{\boldsymbol{x}_t}\,f\left(\boldsymbol{x}_t\right)\right\Vert}\quad(10) xt+1=∥∥∥∥xt−ηt(1+∥∇xtf(xt)∥xt⊤∇xtf(xt))(I−xtxt⊤)∇xtf(xt)∥∥∥∥xt−ηt(1+∥∇xtf(xt)∥xt⊤∇xtf(xt))(I−xtxt⊤)∇xtf(xt)(10)
故弄玄虚
有意思的地方讲完了,下面讲一下没有意思的地方了。对NLP有稍微深入一点了解的读者(看过Word2Vec的数学原理,推导过常规模型的梯度)应该会觉得,上面前两节内容并没有什么很深奥的内容,第三节的几何解释和学习率调节有点新颖,但也是有迹可循的内容。不过要是去看原论文的话,那感觉可能就完全不一样了,作者用“概率分布”、“黎曼流形上的优化”等语言,把上述本该比较容易理解的内容,描述得让人云里雾里,深有故弄玄虚之感。
首先,我最不理解的一点是,作者在一开始就做了一个不合理的假设(将词向量连续化),然后花了不少篇幅来论证 p ( v ∣ u ) ∼ e cos ( v , u ) p(v|u)∼e^{\cos(v,u)} p(v∣u)∼ecos(v,u)和 p ( u ∣ d ) ∼ e cos ( u , d ) p(u|d)∼e^{\cos(u,d}) p(u∣d)∼ecos(u,d)对应着Von Mises–Fisher分布。然后呢?就没有然后了,后面的所有内容跟这个Von Mises–Fisher分布可以说没有半点关系,所以不理解作者写这部分内容的目的是什么。
接着,在优化那部分,作者说带约束 ‖ x ‖ = 1 ‖x‖=1 ‖x‖=1的 f ( x ) f(x) f(x)最小化问题不能用梯度下降,所以只能用“黎曼梯度下降”,然后就开始“炫技”了:先说说黎曼流形,然后给出一般的指数映射,再然后给出黎曼梯度,一波高端操作下来,最后却只保留了一个大家都能懂的方案: x = θ ‖ θ ‖ x=\frac{θ}{‖θ‖} x=‖θ‖θ。这时我就很“服气”了,虽然作者的逻辑和推导都没有毛病,但是一波操作下来最后却给看众一个 x = θ ‖ θ ‖ x=\frac{θ}{‖θ‖} x=‖θ‖θ的朴素结果,那为什么不一开始就直接讨论 f ( x = θ ‖ θ ‖ ) f(x=\frac{θ}{‖θ‖}) f(x=‖θ‖θ)的优化呢?非得要去黎曼流形上面把普通读者绕晕?
此外,我说的比较有意思的部分,就是更新量的几何解释以及得到的调节因子,作者也说得挺迷糊的。总之,笔者认为,论文的理论推导部分,很多地方都充斥着很多不必要的专业术语,无端加深了普通看众的理解难度。
最后强调一下,笔者从来不反对“一题多解”,也不反对将简单的内容深化、抽象化,因为“深化”、“抽象化”确实也可能获得更全面的认识,或者能显示各个分支之间的联系。但是这种“深化”、“抽象化”应该要建立在一个大多数人都能理解的简单解的基础上进行的,而不是为了“深化”、“抽象化”而特意舍去了大多数人能理解的简单解。
实验结果
吐槽归吐槽,在实验部分,JoSE做得还是很不错的。首先给出了JoSE的高效的C语言实现:
Github:https://github.com/yumeng5/Spherical-Text-Embedding
我试用了一下,训练确实很快速,训练好的词/句向量结果可以用gensim的KeyedVectors加载。另外我还看了一下源代码,很简练清晰,也方便做二次修改。
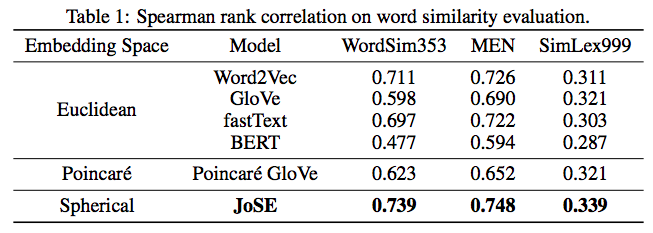
至于实验结果,论文给出的词/句向量评测上面,JoSE也是比较领先的:

文章总结
本文分享了一个发表在NeurIPS 2019的文本向量模型JoSE,着重讲了一下笔者觉得有启发性的部分,并用自己的方法给出了推导过程。JoSE可以认为是Doc2Vec的自然变种,在细微之处做了调整,并且在优化方法上提出了作者自己的见解,除却一些疑似故弄玄虚的地方之外,还不失为一个可圈可点的工作。
























 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








