支持向量机

最新推荐文章于 2024-08-29 16:42:17 发布

Frisk¹²³

最新推荐文章于 2024-08-29 16:42:17 发布

阅读量692

点赞数 14

文章标签：支持向量机算法机器学习

本文链接：https://blog.csdn.net/weixin_43657889/article/details/139597535

版权

支持向量机（SVM）是一种用于分类和回归分析的监督学习模型。SVM的核心思想是通过找到一个最佳的超平面，将数据分成不同的类别，并最大化分类边界与样本点之间的距离。这个最佳超平面是通过支持向量（Support Vectors）来确定的。

一、介绍

SVM 的基本概念

超平面 (Hyperplane)：在n维空间中，一个n-1维的平面称为超平面。例如，在二维空间中，超平面是一条直线；在三维空间中，超平面是一个平面。
支持向量 (Support Vectors)：在样本中离超平面最近的点。这些点对确定最佳超平面有重要影响。
间隔 (Margin)：支持向量与超平面之间的距离。SVM的目标是最大化这个间隔，以提高模型的泛化能力。

SVM 的基本原理

1. 线性可分数据的 SVM

对于线性可分的数据，SVM 的目标是找到一个能够将不同类别的数据点完全分开的超平面。这个超平面可以用如下形式表示：

$w\cdot x+b=0$

其中， $w$ 是超平面的法向量， $b$ 是偏置项， $x$ 是输入特征向量。为了保证所有数据点都被正确分类，我们希望：

$y_{i}(w\cdot x_{i}+b)>=1, \forall i$

其中， $y_{i}\in \left \{1, -1 \right \}$ 是数据点 $x_{i}$ 的标签。

2. 最大化间隔

SVM 的目标不仅是找到一个可以分开数据的超平面，还要找到使得支持向量到超平面的距离（间隔）最大的那个超平面。这个间隔可以表示为：

$margin=\frac{2}{\left \| w \right \|}$

为了最大化这个间隔，我们可以将优化问题表示为：

$minimize \ \frac{1}{2}\left \| w \right \|^{2} \ subject \ to \ y_{i}(w \cdot x_{i}+b)>=1, \forall i$

这个优化问题是一个凸二次优化问题，可以通过拉格朗日乘子法来求解。

3. 拉格朗日对偶性

为了求解这个优化问题，我们引入拉格朗日乘子 $\alpha_{i}>=0$ ，构造拉格朗日函数：

$L(w, b, \alpha )=\frac{1}{2}\left \| w \right \|^{2}-\sum_{i=1}^{n}\alpha_{i}\left [ y_{i}(w \cdot x + b)-1 \right ]$

通过对 $w$ 和 $b$ 求偏导并令其为零，可以得到优化问题的对偶形式：

$maximize \ \sum_{i=1}^{n}\alpha_{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_{i}\alpha_{j}y_{i}y_{j}(x_{i} \cdot x_{j})$

$subject \ to \ \sum_{i=1}^{n}\alpha_{i}y_{i}=0,\ \ \ \ \alpha_{i}>=0, \ \ \ \ \forall i$

通过求解这个对偶问题，我们可以得到最优的 $\alpha_{i}$ 。支持向量对应的 $\alpha_{i}>0$ 。

4. 非线性数据的 SVM

对于非线性可分的数据，SVM 通过引入核函数将数据映射到更高维的空间中，使其在高维空间中线性可分。常用的核函数包括：

线性核： $K(x_{i},x_{j})=x_{i}\cdot x_{j}$
多项式核： $K(x_{i},x_{j})=(x_{i}\cdot x_{j}+c)^{d}$
高斯核（RBF核）： $K(x_{i},x_{j})=e^{-\gamma \left \| x_{i}- x_{j} \right \|^{2}}$

通过核函数，优化问题的对偶形式变为：

$maximize \ \sum_{i=1}^{n}\alpha_{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_{i}\alpha_{j}y_{i}y_{j}K(x_{i},x_{j})$

$subject \ to \ \sum_{i=1}^{n}\alpha_{i}y_{i}=0,\ \ \ \ \alpha_{i}>=0, \ \ \ \ \forall i$

通过求解这个优化问题，我们可以得到最优的 $\alpha_{i}$ 和决策函数：

$f(x)=sign(\sum_{i=1}^{n}\alpha_{i}y_{i}K(x_{i},x)+b)$

5. 松弛变量和软间隔 SVM

在实际应用中，数据往往不是完全线性可分的。为了处理这种情况，SVM 引入了松弛变量 $\xi _{i}>=0$ ，允许某些数据点违反间隔约束。优化目标变为：

$minimize \ \frac{1}{2}\left \| w \right \|^{2}+C\sum_{i=1}{n}\xi_{j}$

$subject \ to \ y_{i}(w \ cdot x_{i}+b)>=1-\xi_{i}, \ \ \ \ \xi_{i}>=0, \ \ \ \ \forall i$

其中， $C$ 是正则化参数，用于权衡间隔最大化和误分类惩罚。

二、代码实践

SVM代码实现

class SVM:
    def __init__(self, lr=0.001, lambda_param=0.01, num_step=1000):
        '''

        :param lr: 学习率
        :param lambda_param: 正则化参数
        :param num_step: 步数
        '''
        self.lr = lr
        self.lambda_param = lambda_param
        self.num_step = num_step
        self.w = None
        self.b = None

    def fit(self, X, y):
        #初始化权重和偏置
        num_samples, num_features = X.shape
        self.w = np.zeros(num_features)
        self.b = 0

        #将标签从 0/1 转换为 -1/1。SVM 要求标签为 -1 和 1。
        y_ = np.where(y <= 0, -1, 1)

        #梯度下降
        for _ in range(self.num_step):
            for idx, x_i in enumerate(X):
                #检查样本是否满足分类条件,更新权重和偏置
                if y_[idx] * (np.dot(x_i, self.w) - self.b) >= 1:
                    self.w -= self.lr * (2 * self.lambda_param * self.w)
                else:
                    self.w -= self.lr * (2 * self.lambda_param * self.w - np.dot(x_i, y_[idx]))
                    self.b -= self.lr * y_[idx]

    def predict(self, X):
        pred = np.dot(X, self.w) + self.b
        return np.sign(pred)

数据生成代码

def create_data():
    from sklearn.datasets import make_blobs
    X, y = make_blobs(n_samples=50, centers=2, random_state=42)
    y = np.where(y == 0, -1, 1)
    return X, y

生成的数据集

可视化结果代码

def show_data(X, y):
    X1, X2 = X[y==-1], X[y==1]
    print(X1)
    plt.scatter(X1[:, 0], X1[:, 1], color='blue')
    plt.scatter(X2[:, 0], X2[:, 1], color='red')
    plt.show()

def visualize_svm(X, y, svm):
    def get_hyperplane_value(x, w, b, offset):
        return (-w[0] * x + b + offset) / w[1]

    plt.scatter(X[:, 0], X[:, 1], marker='o', c=y)

    ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()

    x = np.linspace(xlim[0], xlim[1], 30)
    y_pred = get_hyperplane_value(x, svm.w, svm.b, 0)
    margin_plus = get_hyperplane_value(x, svm.w, svm.b, 1)
    margin_minus = get_hyperplane_value(x, svm.w, svm.b, -1)

    plt.plot(x, y_pred, 'k-')
    plt.plot(x, margin_plus, 'k--')
    plt.plot(x, margin_minus, 'k--')

    plt.legend()
    plt.show()

完整代码

import numpy as np
import matplotlib.pyplot as plt

def create_data():
    from sklearn.datasets import make_blobs
    X, y = make_blobs(n_samples=50, centers=2, random_state=42)
    y = np.where(y == 0, -1, 1)
    return X, y

def show_data(X, y):
    X1, X2 = X[y==-1], X[y==1]
    print(X1)
    plt.scatter(X1[:, 0], X1[:, 1], color='blue')
    plt.scatter(X2[:, 0], X2[:, 1], color='red')
    plt.show()

def visualize_svm(X, y, svm):
    def get_hyperplane_value(x, w, b, offset):
        return (-w[0] * x + b + offset) / w[1]

    plt.scatter(X[:, 0], X[:, 1], marker='o', c=y)

    ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()

    x = np.linspace(xlim[0], xlim[1], 30)
    y_pred = get_hyperplane_value(x, svm.w, svm.b, 0)
    margin_plus = get_hyperplane_value(x, svm.w, svm.b, 1)
    margin_minus = get_hyperplane_value(x, svm.w, svm.b, -1)

    plt.plot(x, y_pred, 'k-')
    plt.plot(x, margin_plus, 'k--')
    plt.plot(x, margin_minus, 'k--')

    plt.legend()
    plt.show()

class SVM:
    def __init__(self, lr=0.001, lambda_param=0.01, num_step=1000):
        '''

        :param lr: 学习率
        :param lambda_param: 正则化参数
        :param num_step: 步数
        '''
        self.lr = lr
        self.lambda_param = lambda_param
        self.num_step = num_step
        self.w = None
        self.b = None

    def fit(self, X, y):
        #初始化权重和偏置
        num_samples, num_features = X.shape
        self.w = np.zeros(num_features)
        self.b = 0

        #将标签从 0/1 转换为 -1/1。SVM 要求标签为 -1 和 1。
        y_ = np.where(y <= 0, -1, 1)

        #梯度下降
        for _ in range(self.num_step):
            for idx, x_i in enumerate(X):
                #检查样本是否满足分类条件,更新权重和偏置
                if y_[idx] * (np.dot(x_i, self.w) - self.b) >= 1:
                    self.w -= self.lr * (2 * self.lambda_param * self.w)
                else:
                    self.w -= self.lr * (2 * self.lambda_param * self.w - np.dot(x_i, y_[idx]))
                    self.b -= self.lr * y_[idx]

    def predict(self, X):
        pred = np.dot(X, self.w) + self.b
        return np.sign(pred)


X, y = create_data()
show_data(X, y)
svm = SVM()
svm.fit(X, y)
visualize_svm(X, y, svm)

运行结果

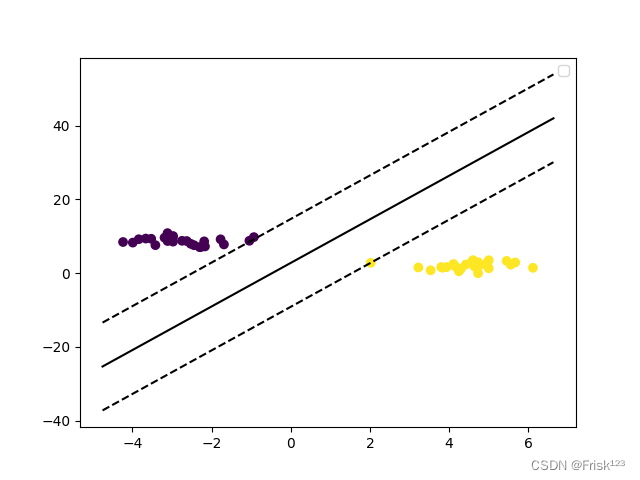
可以看到两类的数据被实线分开，其中在虚线上的数据点即是支持向量、

总结

通过这篇博客，我们了解了支持向量机的基本原理，并使用Python实现了一个简单的SVM分类器。希望这篇博客能帮助你更好地理解SVM，并在实际应用中使用它来解决分类问题。

Frisk¹²³

关注

14
点赞
踩
8

收藏

觉得还不错? 一键收藏
0
评论
支持向量机

超平面 (Hyperplane)：在n维空间中，一个n-1维的平面称为超平面。例如，在二维空间中，超平面是一条直线；在三维空间中，超平面是一个平面。支持向量 (Support Vectors)：在样本中离超平面最近的点。这些点对确定最佳超平面有重要影响。间隔 (Margin)：支持向量与超平面之间的距离。SVM的目标是最大化这个间隔，以提高模型的泛化能力。通过这篇博客，我们了解了支持向量机的基本原理，并使用Python实现了一个简单的SVM分类器。
复制链接

扫一扫