如何进行单个比特的量子层析？（以光子偏振为例）

最新推荐文章于 2024-06-27 00:00:00 发布

往今～

最新推荐文章于 2024-06-27 00:00:00 发布

阅读量523

点赞数 7

文章标签：量子计算

本文链接：https://blog.csdn.net/weixin_43718835/article/details/137381941

版权

（PS：本文仅为个人学习记录，参考的文章或资料会在文末列出）

#目录#

引言
正文

量子态层析的理论模型

量子态层析的实验方案设计

量子态层析的实验数据分析与优化

结语

引言

量子态层析（Quantum state tomography），顾名思义，是一种对量子态的分析方法，即通过将某个未知状态的量子系统投影到已知状态并由得到的测量数据建立密度矩阵，从而得知该量子系统的状态，这与大脑CT的原理类似，也许是因此有了这个"tomography"的名字吧。无论是传统的量子力学还是在如今迅猛发展的量子通信与量子信息处理领域，知悉某个量子系统或者某个量子信号的状态表象都是非常重要的，所以量子态层析这一技术在各大领域发挥着基石一般的重要作用。为了简便起见，这里我们用常见的二能级系统，即光子偏振维度为例，从理论模型，具体的实验过程以及实验数据的后处理进行详细的阐述与说明。

为了更好的理解层析这一过程，首先我们需要对光子偏振、密度矩阵与测量这三个概念做一些直观的了解与认知。

偏振、Stokes参量、庞加莱球与布洛赫球

从宏观上来看，偏振是光的振动随时间的变化轨迹，按照偏振程度可以将经典光束分为非偏振光、部分偏振光和完全偏振光。而完全偏振光又可以分为线偏振光、圆偏振光和椭圆偏振光三类。椭圆偏振光可以看做是一般情况，而线偏振光与圆偏振光则是在特殊取值下的特殊情况，因此我们从经典光束传播的角度出发，建立一般的椭圆偏振光模型：

在传播中的经典光波可以分解为正交的x,y分量，在一般情况下，两正交分量所累积的不同相位会使得光波的振动轨迹随时间呈现出椭圆形状，这里假设这个椭圆模型的旋转角为α，椭圆度为β。

经典光波的传播可做如下表示：

$E_{x}=E_{0x}cos\left ( wt-kz+\varphi _{x} \right )$

$E_{y}=E_{0y}cos\left ( wt-kz+\varphi _{y} \right )$

这里我用的是三角函数表示而非复数，是为了方便进行偏振椭圆方程式的推导。假设两正交分量之间的相位差为φ = φy - φx，那么可以进一步计算得：

$\frac{E_{y}}{E_{0y}}=cos\left ( wt-kz+\varphi _{x} \right )cos\varphi -sin\left ( wt-kz+\varphi _{x} \right )sin\varphi$

$\frac{E_{x}}{E_{0x}}=cos\left ( wt-kz+\varphi _{x} \right )$

消去含有参量t的余弦函数，先两边取平方再用已知量代入，运算的时候应尽量避免开根号以及作商等运算。在进行一番运算后，我们可以得到偏振态的椭圆方程:

$\frac{E_{x}^{2}}{E_{0x}^{2}}+\frac{E_{y}^{2}}{E_{0y}^{2}}-2\frac{E_{x}}{E_{0x}}\frac{E_{y}}{E_{0y}}cos\varphi =sin^{2}\varphi$

为了能够进一步确定椭圆的两个状态参数，即方位角和椭偏度，我们需要对这个椭圆方程进行一些公式推导，由于步骤比较多，这里我就不用latex敲了，直接上图片：

在下的数学不是很好，感兴趣的小伙伴或许可以尝试用更为简便的方法得到最后这两个表达式：

$tan2\alpha =\frac{2E_{0x}E_{0y}cos\varphi }{E_{0x}^{2}-E_{0y}^{2}}=tan2\delta cos\varphi$

$sin2\beta =\frac{2E_{0x}E_{0y}sin\varphi }{E_{0x}^{2}+E_{0y}^{2}}=sin2\delta sin\varphi$

有了这两个表达式，偏振态的振动方位以及椭偏度可以确定下来，再结合x-y分量的相位差以确定旋向，那么椭圆偏振态可以唯一确定。那么，下面让我们看看从斯托克斯参量和基本庞加莱球的角度是如何来描述偏振态的吧。

1852年，Stokes提出了用四个参量来描述光波强度和偏振态的方法，这四个参量均是光强的时间平均值，而这里我们仍然会用一些简化的表达式来描述，可能会不符合数学规范，但这里仅求定性说明问题。这四个量组成了一个数学矢量：

$S=\begin{bmatrix} S_{0}\\ S_{1}\\ S_{2}\\ S_{3} \end{bmatrix}=\begin{bmatrix} E_{0x}^{2}+E_{0y}^{2}\\ E_{0x}^{2}-E_{0y}^{2}\\ 2E_{0x}E_{0y}cos\varphi \\ 2E_{0x}E_{0y}sin\varphi \end{bmatrix}$

其中第一个参量S0表示光波的总强度，S1表示光波的x方向强度分量，而S2和S3则分别表示45°和右旋方向的光波强度分量。当然Stokes参量的表示方法还有很多种，但万变不离其宗，表现形式随各异，但每个量所体现的物理含义是一样的，均为光波在三个不同方向的强度投影。至于为什么这三个参量可以构成测量偏振态的正交完备集，以及为什么是用上面的表达式去体现各个方向的光波强度分量，在下暂时还没想明白。先假设这些是既定法则，在准单色非相干条件下，我们可以得到这样的关系式：

$S_{0}^{2}\geqslant S_{1}^{2}+S_{2}^{2}+S_{3}^{2}$

当光波为非偏振光或者部分偏振光时，总光强是大于三个方向的偏振分量光强；而仅当光波为完全偏振光时，等号才成立。而具有任意均匀偏振态的完全偏振光均能够用斯托克斯矢量来表示。对于完全偏振光而言，斯托克斯参量构成的等式可以用图表示为以S1,S2和S3为坐标轴，半径为S0的球。如下图所示：

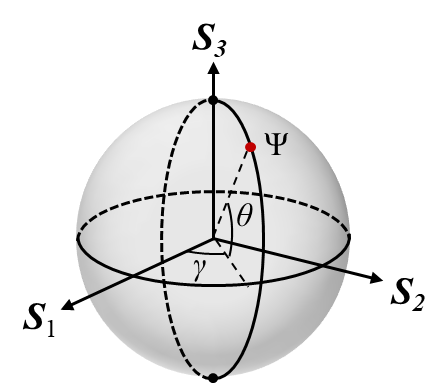
球面上的每一点均表示完全偏振光，而球内的点则表示不完全偏振光。类似于用经纬度表示地球坐标，庞加莱球上的每一点笛卡尔坐标也可以由两个角度坐标θ和γ表示：

$\overrightarrow{\Psi }=\left ( S_{0}cos\theta cos\gamma, S_{0}cos\theta sin\gamma, S_{0}sin\theta \right )$

也即： $S_{1}=S_{0}cos\theta cos\gamma ,S_{2}=S_{0}cos\theta sin\gamma, S_{3}=S_{0}sin\theta$

根据笛卡尔坐标系与球坐标系之间的对应关系，我们可以求解出表征球面上某个点的经纬角度

$\gamma =arctan\frac{S_{2}}{S_{1}}, \theta =arcsin\frac{S_{3}}{S_{0}}$

我们看看这个表达式是不是有些眼熟呢？之前的光波偏振态似乎也有两个角度，一个表示方位角，另一个表示椭偏度，似乎也可以与斯托克斯矢量或者说庞加莱球建立起关系：

$2\alpha =arctan\frac{S_{2}}{S_{1}}, 2\beta =arcsin\frac{S_{3}}{S_{0}}$

也就是说，在庞加莱球面上某一点表征的偏振态，其偏振旋转角是经度的一半，其椭偏度是纬度的一半。在南北两极点处，θ分别为-+pi/2，表明此时为圆偏振，且旋向相反，根据斯托克斯参量的定义：φ>0即北半球为右旋，φ<0即南半球为左旋；所以庞加莱球的北极为右旋圆偏振光，南极为左旋圆偏振光。赤道上的点纬度为0，椭偏度也为0，为水平偏振光。

在此之后的Jones矢量方法也同样是用来描述偏振状态的，其核心思想也是将光子状态用两个偏振正交基来表示，例如x-y，R-L，D-A或者是其他。并将其写成矢量的形式，同时将常见的偏振元件写成矩阵形式，以此将光场的偏振转换与分析全部简化为数学上的矩阵运算。在这里，我们也可以利用这一思想，将庞加莱球上某一点的偏振状态用一组正交基简单表示出来：

$|\Psi >=E_{0x}e^{i\varphi _{x}}|H>+E_{0y}e^{i\varphi _{y}}|V>$

无论哪一种偏振态，拆在基矢上均为振幅以及相位，我们在之前已经做好了一些假设，即φ = φx - φy，同时也对振幅做一个归一化处理，公因数项忽略不计，可以得到：

$|\Psi >=\frac{E_{0x}}{\sqrt{E_{0x}^{2}+E_{0y}^{2}}}|H>+\frac{E_{0y}}{\sqrt{E_{0x}^{2}+E_{0y}^{2}}}e^{i\varphi }|V>$

现在我们来看看此前定义的庞加莱球上的参数与这个表达式的关系。假设纬度线从赤道转动到北极，在我们定义的坐标下，纬度θ增加了pi/2。x-y分量之间的相位差从赤道上的 φ=0 变化到了北极点的 φ=pi/2。也就是说φ = θ。而x-y方向振幅之间的权重会影响光波最终的偏振方向，但我们知道庞加莱球上的经度坐标γ是振动方向改变角度的两倍。

$\varphi =\theta ,tan\frac{\gamma }{2}=\frac{E_{0y}}{E_{0x}}$

当然也可以用我们前面推导的椭圆偏振态的式子计算，注意φ=0，因为这里是在赤道上假设经度坐标的改变，相当于代入一个特殊值。整理一下上面的表达式，我们可以得到：

$|\Psi >=cos\frac{\gamma }{2}|H>+sin\frac{\gamma }{2}e^{i\theta}|V>$

其实这个表达式与我在论文中看到的很多都有些不相同，无论是坐标定义、基矢和坐标表示上都不太一致，除了这个形式是一样的。如果我的推导有误，还望大佬可以帮我指出。

布洛赫球与庞加莱球基本是相同的，只不过在表述上存在一些差异，即球面上所有的点表示纯态，可以表示为|0>和|1>两基态的线性叠加。如果将|H>作为|0>态，|V>作为|1>态，相应的可以算出另外两条轴上的态，|D> = |0> + |1>,|A> = |0> - |1>,|R> = |0> + i|1>,|L> = |0> - i|1>，这里的虚数i表示相位差为pi/2。那么二能级系统的任意纯态可以表示为：

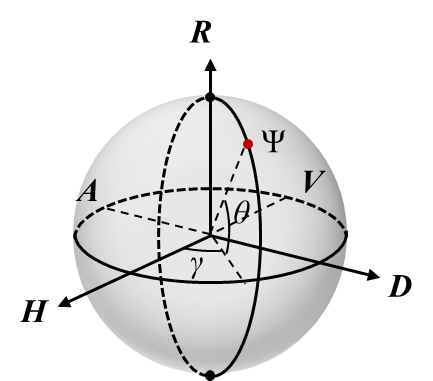
$|\Psi >=cos\frac{\gamma }{2}|0>+sin\frac{\gamma }{2}e^{i\theta}|1>$

幺正变换相当于对布洛赫球进行旋转，例如半波片的调控相当于令布洛赫球绕D-A轴旋转180°，以及四分之一波片的调控相当于绕H-V轴旋转90°。

密度矩阵（density matrices）

密度矩阵是1927年被科学家提出的一种从数学角度衡量量子状态的方法，因为我们虽然可以用态叠加或波函数的方式表示纯态，但无法用这种方式表示混合量子态。密度矩阵这种方法可以用来描述包括纯态、混合态的任何量子状态。在数学上，如果一个密度矩阵可以由某个量子态的左右矢外积得到，那么说明这个量子态为纯态；如果不能，则为混合态。

而纯态与混合态可以用左右矢外积做如下的表示：

$Pure state: \rho =|\Psi ><\Psi |$

$Unpure state: \rho =\sum_{i}^{}p_{i}|\Psi _{i}><\Psi _{i}|$

也就是说，一个纯态的量子状态等于态矢量的外积，而一个混合的量子状态则等于每个纯态的概率组合。密度矩阵具有几个性质，厄米性、幺迹性、半正定性。厄米性指的是密度矩阵的共轭转置仍然等于其自身；幺迹性指的是密度矩阵的对角元素之和为1，也即是说矩阵的本征值概率之和为1。半正定性说的是矩阵的所有测量值均大于或等于0。纯态的密度矩阵具有幂等性，即矩阵的幂次方等于其自身，但混合态不具有这一性质。这些性质我并没有证明，感兴趣的小伙伴可以自行证明。

前面假设了光子偏振|H>为|0>纯态，|V>为|1>纯态。现在用一组二维正交向量基矢做如下假设：

$|H>=\begin{bmatrix} 1\\ 0 \end{bmatrix}=|0>$ $|V>=\begin{bmatrix} 0\\1 \end{bmatrix}=|1>$

那么根据纯态密度矩阵的定义方式，我们可以计算到|H>纯态与|V>纯态的密度矩阵：

$\rho _{H} = |H><H|=\begin{bmatrix} 1\\ 0 \end{bmatrix}\begin{bmatrix} 1 & 0 \end{bmatrix}=\begin{bmatrix} 1 &0 \\ 0 & 0 \end{bmatrix}$ $\rho _{V}=\begin{bmatrix} 0 &0 \\ 0&1 \end{bmatrix}$

这里需要注意的是，右矢为列向量，左矢为行向量，且左矢与右矢之间互为共轭转置。这一点在计算的时候很容易被忽略。在这里我们可以举一个明确的例子从密度矩阵的角度去看纯态和混合态。

纯态|D>的密度矩阵： $\rho _{D}=|D><D|=\frac{1}{2}\begin{bmatrix} 1\\ 1 \end{bmatrix}\begin{bmatrix} 1 & 1 \end{bmatrix}=\frac{1}{2}\begin{bmatrix} 1 & 1\\ 1 & 1 \end{bmatrix}$

纯态|A>的密度矩阵： $\rho _{A}=\frac{1}{2}\begin{bmatrix} 1\\-1 \end{bmatrix}\begin{bmatrix} 1 & -1 \end{bmatrix}=\frac{1}{2}\begin{bmatrix} 1& -1\\ -1 & 1 \end{bmatrix}$

假设存在一个混合量子状态，由概率相等的|D>,|A>两种纯态组合而成，那么其密度矩阵可以写为

$\rho _{ms}=\frac{1}{2}\rho _{D}+\frac{1}{2}\rho _{A}=\frac{1}{2}\begin{bmatrix} 1 & 0\\ 0 &1 \end{bmatrix}$

从上面纯态与混合态的密度矩阵可以看出来，纯态的密度矩阵是可以写成态矢量的左右矢的外积，而混合态则不能，这与开头所说的性质是一致的。这里的混合态需要与纯态中的态叠加概念区分开，两者的区别如果从数学上来看，就是态叠加得写成两个态矢量的和，再求取密度矩阵；而混合态则是将两个纯态求解出密度矩阵后再以概率相加。若是从物理的角度来看，量子态叠加是指一个光子会同时存在于A和B两种状态，并且若是被测量，这种叠加态会以一定概率坍塌为确定的状态A或B，坍缩到这两状态的概率和为1。而混合态则更像是两个确定状态的组合，这种混合状态不会因为测量而被影响。如果平方之后开根号再乘上系数，纯态是等于1但是混合态小于1，这应该也可以作为一个判断依据吧。（小声：我还没证明，慎用，慎用）

测量（Measure）

测量指的是将待测的量子态往某个基上投影，物理上对应于用光学元件与光量子态相互作用。例如光子偏振，通常用波片组合并结合检偏器进行检测；而对于光OAM量子态，则通常是用具有共轭螺旋相位的全息相位进行检测。在有关的量子实验中，我们每次测量通常是一个符合计数值，而在理论上，我们的测量对应于下面的表达式：

$P=<\varphi _{p}|\rho |\varphi _{p}>=tr\left ( \rho|\varphi _{p}><\varphi _{p}| \right )$

假如这里的φp为为H，那么上面的表达式得到的便是密度矩阵在水平这一基矢上的投影数值。而在下面画出来的实验装置中，需要将QWP与polarization均设置为水平方向。测量其他基矢的投影也是用类似的方法。

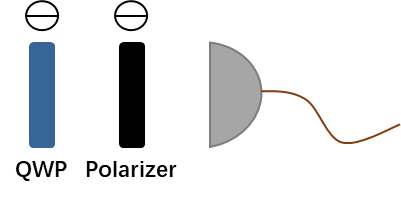
但是这里存在一个实验装置校准的问题，也就是说需要将实验上转动波片的动作与理论计算的数值对应上，也即计算上用的是H基矢，实验上需要让水平偏振的光子通过。

正文

历经种种推导证明，终于来到了我们的正文部分。这里我以光子偏振维度为例，从量子态层析的理论模型、量子态层析的实验方案实验设计和层析的实验数据分析与优化这三个角度来介绍层析。首先说明这个例子相对比较简单，很多以前的论文上都可以检索到，写在这里是为了方便自己学习，常看常新。至于更复杂的层析....我还不会.... 😭.jpg

量子态层析的理论模型

层析的目标是要测量一个未知量子状态的密度矩阵，而根据转化的思想，我们可以将无法直接测量得到的量转化为状态已知的量。这里便是如此，将密度矩阵分别投影在H,V,D,A,R,L上，根据测量得到的数值重建密度矩阵ρ。

就像我们需要知道布洛赫球上|Φ>的态矢量以计算出密度矩阵，就需要将其投影到H-V，D-A和R-L轴上。但在实际的测量中，我们通常仅需要测其中四个即可，其中三个向量分别对应三个轴的数值，而多出来的一个值则用来归一化概率。那么现在，我们开始从理论上跑一跑这个过程：

$\rho =\frac{1}{2}\sum_{i=0}^{3}\sigma _{i}S_{i}$

四个泡利矩阵是已知的，分别为:

$\sigma _{0}=I=\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix},\sigma _{1}=\begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix},\sigma _{2}=\begin{bmatrix} 0 &-i \\ i & 0 \end{bmatrix},\sigma _{3} = \begin{bmatrix} 1 & 0\\ 0 & -1 \end{bmatrix}$

根据上面的式子，密度矩阵可以写为包含未知参数S0,S1,S2和S3的未知矩阵：

$\rho =\begin{bmatrix} \frac{S_{0}+S_{3}}{2} &\frac{S_{1}-iS_{2}}{2} \\ \frac{S_{1}+iS_{2}}{2} & \frac{S_{0}-S_{3}}{2} \end{bmatrix}$

(1) 让任意待测光子的N个相同副本通过方向水平|H>的检偏器，并记录其通过的光子数量：

$n_{0}=Ntr(\rho \mu _{0})=N<0|\rho |0>=\frac{N}{2}\left ( S_{0}+S_{3} \right )$

(2) 让任意待测光子的N个相同副本经过方向竖直|V>的检偏器，并记录其通过的光子数量：

$n_{1}=Ntr(\rho \mu _{1})=N<1|\rho |1>=\frac{N}{2}(S_{0}-S_{3})$

(3) 让任意待测光子的N个相同副本通过45°方向的检偏器，并记录其通过的光子数量：

$n_{2}=Ntr(\rho \mu _{2})=N<+|\rho |+>=\frac{N}{2}(S_{0}+S_{1})$

(4) 让任意待测光子的N个相同副本通过右旋方向的波片，并记录其通过的光子数量：

$n_{3}=Ntr(\rho \mu _{3})=N<L|\rho |R>=\frac{N}{2}(S_{0}+S_{2})$

最终计算得到密度矩阵与测量值的关系如下：

$\rho =\begin{bmatrix} \frac{n_{0}}{N} &(\frac{n_{2}}{N}-\frac{n_{0}+n_{1}}{2N})-i(\frac{n_{3}}{N}-\frac{n_{0}+n_{1}}{2N}) \\ (\frac{n_{2}}{N}-\frac{n_{0}+n_{1}}{2N})+i(\frac{n_{3}}{N}-\frac{n_{0}+n_{1}}{2N}) & \frac{n_{1}}{N} \end{bmatrix}$

因为这里的运算比较简单，所以密度矩阵的各个元素可以手推出来。但当情况升级到多个比特上时，就需要用到一些线性代数的方法去进行运算。可以参考一篇叫做measurement of qubits 的PRA文章[1]，你可以不懂量子力学，但不可以不懂数学。要是连数学都不懂，那就会像我一样，只能算明白单个比特......

量子态层析的实验方案设计

实验方案设计其实无非两种思路，第一种思路是依赖现有实验条件去构造三个基矢投影，再多出一个基矢用于归一化概率，再从实验结果去计算与理论值之间的关系；而另一种思路则是从密度矩阵出发，得到构成元素所需要的测量，再从实验测量上去获取并代入计算。两种方式殊途同归，具体实操怎么方便怎么来。

在实验中可能会遇到每次测量会遇上不同程度的抖动的问题，可以通过使用PBS同时测量一对同轴基矢来得到。而对于每组基矢的透过率可能不完全相同的问题，可将所有的正交基矢做一个完备测量以缓解。若是在实验过程中出现了不符合物理规律的数据，那么就需要使用一些优化算法例如极大似然估计来进行实验数据的后处理。[2]

若以第一种思路设计实验方案，即理论跟着实验走。假设实验中可以很顺利的构建出标准基矢H,V,D,A,R,L,那么，我们接下来该怎么去做呢？

既然是理论跟着实验走，那么第一步当然是做实验。实验之前，选好要测量的基矢，如果不确定的话，那就把标准基矢全测了，这样保证没错。

实验装置如下：

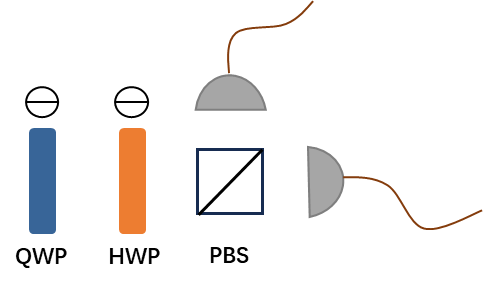
我们以水平方向的探测器为例，通过转动QWP和HWP来检测所有的正交完备基矢：

Basis	QWP(degree)	HWP(degree)
H	0°	0°
V	0°	90°
D	0°	22.5°
A	0°	67.5°
R	45°	22.5°
L	45°	67.5°

如果实验装置不同，那么波片的转动角度也要相应的做出调整[4]，最终都是为了顺利测到这几个状态下的光子数嘛，不要拘泥于形式，得灵活多变呀。

测到了数据之后开始进行下一步运算，具体的计算形式参考理论模型上面的方法，挨个把每次测量所对应的计算表达式写出来，然后通过未知数求解把密度矩阵算出来。不过，上面的计算式用的是现成的泡利矩阵。而前文提及的PRA是用了一种线性变换的方式自行构建出了泡利矩阵。这里其实更为推荐后者。毕竟上面模型里讲的方法不是很好写代码，尤其是拓展到多个量子比特之后。

这里我们假设能够测量标准完备基矢，如果实验条件不满足，仅能测量不标准的完备基矢，实际上步骤也差不多，都是先测完所有的数据，然后进行对应的理论运算，将测量的数值以一定变换规则放进矩阵当中。不过实验者自己得清楚这些不标准的基矢如何表达，不标准并不等于未知。

另外一个思路便是从矩阵本身出发，需要什么算什么。这一点可以参照一篇博客[3], 里面详细写了单个以及两个量子比特的层析，直接从密度矩阵及其特性出发去分析，得到所需的测量期望值与矩阵元素的关系，仅需要在实验中测量出所需期望值即可。以前是全文能看，但现在变成VIP文章了......原文我也没截过图.....so...

量子态层析的实验数据分析与优化

实验数据分析部分也都在上文提到过，即通过线性代数的一些变换来重建密度矩阵。（代码的话后续再放上来，因为还没写......）但如果实验过程中测得的数据存在些问题，就需要利用额外的优化算法去对数据进行处理。

这里简单介绍一下极大似然估计法，其他的优化算法如贝叶斯估计法也行，但是我还没去了解......

极大似然估计（Maximum likelihood estimation, MLE）旨在找到实验结果概率分布函数的参数，使得概率最大。我们用系数给每个实验结果附上一定概率来构建关于每次实验的结果函数，然后每次实验的结果函数相乘，再取对数，最后求导数取极值，因为一阶导数为0的地方一定是极大或者极小值[2]。

先以抛硬币为例子：找到抛掷一枚硬币出现正反面的权重

假设一共抛了N次硬币，每次抛硬币的动作相互独立，抛掷到正面的概率为θ，反面自然是（1-θ），而共有Nh次实验抛到正面，N-Nh次抛到反面。这种情况发生的概率为：

$f\left ( N_{h},N-N_{h};\theta \right )\propto \theta ^{N_{h}}\left ( 1-\theta \right )^{N-N_{h}}$

$l\left ( N_{h},N-N_{h};\theta \right )=N_{h}ln\left ( \theta \right )+\left ( N-N_{h} \right )ln \left ( 1-\theta \right )$

给上面的函数求导数取极值，得到极值点处有：θ=Nh/N

现在我们来看看在层析当中，极大似然估计算法是如何派上用场的。在采完层析的数据之后，我们想要知道什么样的密度矩阵ρ更可能产生我们的测量结果NH,NV,ND,NA,NR,NL;

每次测量的平均值我们定义为：

$\bar{N_{x}}=(N_{x}+N_{x\top })<x|\rho _{test}|x>$

这里面的ρtest是个未知数，x表示某次测量，直角标识表示偏振方向与其垂直的状态。

$p\left ( N_{x};\rho _{test} \right )=e^{-(N_{x}-\bar{N_{x}})^{2}/2\bar{N_{x}}}$

最大化函数 $f\left ( N_{H}...N_{R};\rho _{test} \right )=e^{-(N_{H}-\bar{N_{H}})^{2}/2\bar{N_{H}}}...e^{-(N_{R}-\bar{N_{R}})^{2}/2\bar{N_{R}}}$ 以找到真实的密度矩阵。代码还没写，写了再说。至于更高比特层析的MLE，还没学会....待我github一波先。

结语

从光子的维度上看，偏振仅有两个能级状态，只能凭借相互正交的两个偏振状态（H，V）或（D，A）或（R，L）张成二维的希尔伯特空间。这实际上限制了量子通信和量子信息处理中的一些实际应用，例如光子偏振仅能用于构建单比特的逻辑门。而其他的光子维度例如OAM便具有理论上无界的离散级，可张成N维的希尔伯特空间，在量子通信和高维量子信息处理领域具有很大的潜力。（当然这是后话......OAM的量子态层析我也还没做出来....不然就不会写这么多了....）

结语其实也没啥好结的，上面写的东西其实也不是很难，但我写了很久，虽然也不知道我写这些干嘛......既然都写了，那还是希望能够有点什么用处。

希望大家工作顺利，嗯...，搞科研的也科研顺利.......

参考文献：

[1] James, D. F. V. , Kwiat, P. G. , Munro, W. J. , & White, A. G. . (2001). Measurement of qubits. Physical Review A, 64(6), 052312.

[2] PPT：State and Process tomography

[3]量子态层析(quantum state tomography)-CSDN博客

[4] Karimi, E. . (2017). Quantum Cryptography with Structured Photons. Asia Communications & Photonics Conference.

往今～

关注

7
点赞
踩
7

收藏

觉得还不错? 一键收藏
1
评论
如何进行单个比特的量子层析？（以光子偏振为例）

量子态层析（Quantum state tomography），顾名思义，是一种对量子态的分析方法，即通过将某个未知状态的量子系统投影到已知状态并由得到的测量数据建立密度矩阵，从而得知该量子系统的状态，这与大脑CT的原理类似，也许是因此有了这个"tomography"的名字吧。无论是传统的量子力学还是在如今迅猛发展的量子通信与量子信息处理领域，知悉某个量子系统或者某个量子信号的状态表象都是非常重要的，所以量子态层析这一技术在各大领域发挥着基石一般的重要作用。
复制链接

扫一扫