本文转载自:https://zhidao.baidu.com/question/528267710.html
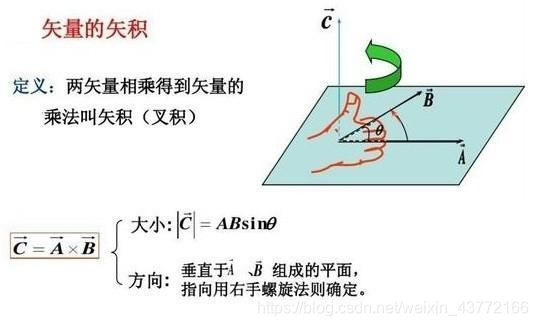
a×b的方向:四指由a开始,指向b,拇指的指向就是a×b的方向,垂直于a和b所在的平面;
b×a的方向:四指由b开始,指向a,拇指的指向就是b×a的方向,垂直于b和a所在的平面;
a×b的方向与b×a的方向是相反的,且有:a×b=-b×a。
注:向量积≠向量的积(向量的积一般指点乘)
一定要清晰地区分开向量积(矢积)与数量积(标积)
扩展资料:
叉乘满足的基本的性质如下:
向量a×向量b=向量0 , 因为夹角是0, 所以平行四边形面积也是0, 即叉积长度为0。
向量a×向量b =−(向量b×向量a), 等式两边的叉积等大反向, 模长因为平行四边形不变而相同, 方向因为右手法则旋转方向相反而相反。
(λ向量a)×向量b=λ(向量a×向量b ), 这点比较好想, 因为:
①正数λ数量乘不会影响向量a的方向, 所以左右的叉积方向一样; 负数λ使得向量a反向了, 但也使得左右叉积方向相反。
②对向量a进行缩放, 平行四边形面积也同等缩放。








 本文详细解析了向量叉乘的定义与特性,包括右手定则确定方向、向量积的性质及其与数量积的区别。并通过实例说明了叉乘满足的基本性质。
本文详细解析了向量叉乘的定义与特性,包括右手定则确定方向、向量积的性质及其与数量积的区别。并通过实例说明了叉乘满足的基本性质。
















 2047
2047

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








