图片的仿射，投影（透视）变换

参考：https://www.cnblogs.com/vincentcheng/p/7191014.html、《opencv算法精解》（张平编著）
下面提到的（x，y）是原始四边形图片的四个角点

仿射变换

平移，放大/缩小、旋转

公式表示：x,y是原来坐标值，前面的是变化后坐标

上面公式根据矩阵乘法可改成下面

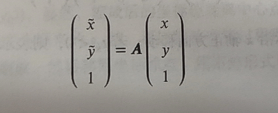
平移矩阵

缩放矩阵

下面是以坐标原点为基准位置对图像坐标进行缩放，若想以想要缩放的图像为

以图片为中心（x0,y0）进行缩放

旋转矩阵

α在逆时针情况下为正


通过上面两个式子可得到下面的矩阵关系

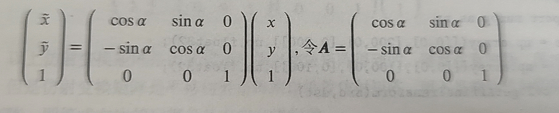
投影（透视）变换

透视变换: 透视变换将图像投影到一个新的视平面，是二维到三维再到另一个二维(x’, y’)空间的映射。
透视变换前两行和仿射变换相同，第三行用于实现透视变换。透视变换前后，原来共线的三个点，变换之后仍然共线

从上面的矩阵形式，看出矩阵参数的作用范围

转化关系理解为
1、相当与将最初的二维的（x，y）点映射到三维空间（x，y，z），这一步就会出现无数中情况，只要有四个点分别在垂直于x，y平面且过原坐标点的四条直线上就行；为了计算方便可以设定z的值为任何一个常数，但不能将原始的z和预测的z都设置常数，；
2、同理将这个三维空间的（x，y，z）转化为另一个（x‘，y’，z‘）
3、（x‘，y’，z‘）使得转化后的点在x-y平面的投影是目的坐标点（x’，y‘）
再对三维空间中的点映射到新的二维空间，原始坐标值或变化后的坐标值，都相当于图片投影在坐标x，y轴上的投影图片四个角的坐标，因此对于z轴没有要求，也就是说z的值是任意值，但为了计算可将预测四个点坐标z设置为一个常数或原始的四个点坐标z设置为一个常数，但不能同时设置为常数。如果都设置为常数，那么两个四点所在平面必定平行。
对于矩阵的计算所有等式来看，为了求得变换矩阵A，将四个坐标的矩阵等式展开后得到12个等式，下面是一个等式展开

最终的等式会出现**：8个关于预测x，y的等式，4个关于预测z的等式**，其中a有下标的，都是是想要求的数据，从上面分析得知有一组z为自己设置的常数，如上图，其他文中提到将z=1，是将A矩阵中的参数
现在的未知参数有4个z，9个a，共13个未知数，但只有12个等式。因为得到一个投影到x-y平面相同投影的四个点z是可以沿着z轴方向平移的。
这时只要设定一个z的值，其他12个未知参数也就确定了，也可以确定a中的一个值，然后计算对应的几个z都能变成唯一值。（在opcv中的矩阵就是把a₃₃设置为1），这样做只要能得到正确的x，y坐标值，就没有问题。
仿射变换和透视变换的关系，仿射变换将最初的z都设置为1，而最终得到的预测值的x，y也都可以除以z的值得到（x‘，y’，1）的形式，相当于仿射变换的四个点的z可以都是1 。如下图仿射变换（m₃₁和m₃₂为0，m₃₃是1）