【单目3D目标检测】MonoGround论文精读与代码解析

Preface

Qin Z, Li X. MonoGround: Detecting Monocular 3D Objects From the Ground[C]. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022: 3793-3802.
Paper
Code

Abstract

从单幅二维图像中获取三维信息本质上比较困难，主要有以下三点原因：

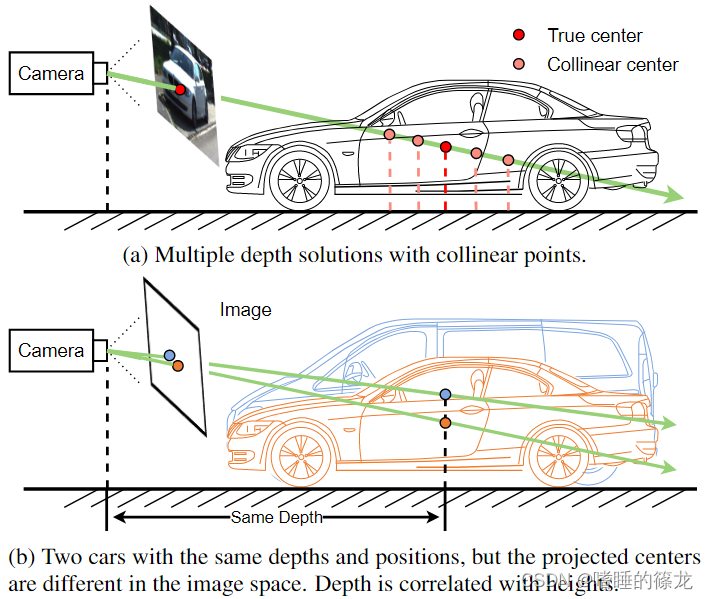
• 一对多的映射关系：从2D到3D的映射是一个不适定（ill-posed）的问题，因为2D图像平面中的一个位置对应于所有共线的3D位置，这些位置存在于从相机中心到2D位置的射线中。如下图中(a)所示，这种一对多的特性使得预测物体的深度非常困难
• 深度在图片中的表达与物体的实际高度有关：对于两个深度和位置相同的物体，如果高度不同，则在相机平面的投影中心会不同，如下图(b)所示，这样，深度的学习就必须克服对象不相关属性的干扰
• 基于CenterNet的单目3D目标检测算法，物体的所有信息（包括深度）用一个点来表示，那么在训练过程中，对深度的监督是非常稀疏的，导致深度估计的学习不足（假设一个图像中有两辆车，那么深度图上只有两个点会被训练，而深度图上的所有其他点都被忽略）

 

Contributions

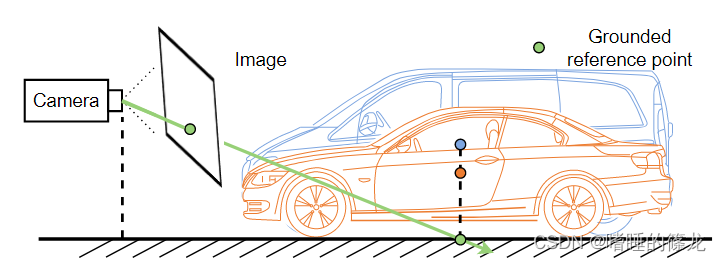
针对上述问题，本文提出在单目3D目标检测任务之前引入地平面先验（Ground Plane Prior）。在地平面先验的情况下，病态的2D到3D映射成为一个具有唯一解的适定问题。唯一解由相机射线与地平面的交点决定。深度表达不再与物体高度相关，如图2所示

本工作的主要贡献可以概括如下:

• 提出在单目3D目标检测之前引入地平面，可以缓解ill-posed映射，消除深度的不相关关系，同时提供密集的深度监督，而不需要任何额外的数据，如LiDAR、立体和深度图像
• 提出了一种深度对齐训练策略，以有效地学习和预测密集接地深度
• 同时，利用稠密预测深度，提出了两阶段深度推断方法，实现了更细粒度的深度估计

单目3D目标检测中的地平面先验：

• 地平面知识在单目3D目标检测中已经有过多次尝试。Mono3D首先尝试使用地平面来生成3D边界框建议，Ground-Aware在几何映射中引入了地平面，并提出了一个接地感知卷积模块来增强检测。在上述工作中，地平面是根据一个固定的规则定义的，例如KITTI上的摄像机高度为1.65米。这样，三维空间中固定高度为-1.65米的所有位置都将构成地平面
• 但是本文则提出了一个可学习地平面先验，它基于一个更合理的假设，即物体应该躺在地面上。只要物体在地面上，地平面可以用物体的三维边界框底面代替。这样，所提出的地平面先验于物体的底面

单目3D目标检测中的深度估计：

• 纯单目3D目标检测中主流的深度估计方法有两种，分别是直接回归方法和基于针孔成像模型的几何投影方法，此外，MonoFlex通过对角成对关键点的几何深度的平均值将几何深度扩展到对角关键点深度。同时，许多研究在深度估计的同时采用了不确定性，得到了较好的结果
• 本文则在地平面先验的帮助下，提出了一种不同于上述方法的新的深度估计方法。它是一种两阶段深度推理方法，可以得到比几何深度更精确的深度估计。此外，所提出的深度估计还可以采用不确定性和对角成对关键点的扩展
   

Problem Definition

单目3D目标检测任务是从单目RGB图像中检测出3D目标（ill-posed）。除了RGB图像，还可以采用标定信息（即摄像机参数矩阵）。具体来说，对于每个物体，都需要：

• 三维位置$(x,y,z)$
• 大小$(h,w,l)$
• 方向$\theta$，在KITTI数据集上，俯仰角和横摇角被视为零，因此只考虑偏航角$\theta$

与上述目标相对应，主流方法将整个任务划分为4个子任务，分别是2D位置（根据投影公式计算出3D位置）、深度、尺寸和方向估计任务。而深度估计是单眼三维目标检测的关键瓶颈，本文的工作专注于精确的深度估计
 

Ground Plane Prior

通过3D框的标注信息，来获取密集的地平面表示
整个流程如下：

1. 首先利用物体的标注坐标信息，获取底面四个角点的坐标
2. 利用底面四个角点的坐标，在地面随机采样，获得地面的随机采样点$P_{3d}$（此时为3D坐标）
3. 将地面的随机采样点坐标，转换为2D图像坐标

In Paper

为了定义地平面，本文从一个合理的假设开始，即物体位于地面上。这个假设适用于所有常见的物体，如汽车、行人和骑自行车的人。在此假设下，可以用物体三维边界框的底面代替地平面。对于每个对象，我们首先获得3D空间中的底部键点$k_1、k_2、k_3$和$k_4$。然后对由底部关键点组成的三维底面进行随机采样和插值。将$R\in {\mathbb{R}}^{N\times 2}$表示为每个元素为$R_{i,j}\in [0,1]$的随机矩阵。$N$是采样点的个数，采样的密集点可表示为：
$$P_{3d}=R\left[\begin{array}{l}{k}_2-k_1\\ k_4-k_1\end{array}\right]+k_1$$
其中$P_{3d}\in {\mathbb{R}}^{N\times 3}$包含所有采样点。假设$K_{3\times 3}$为摄像机参数矩阵。采样后将这些点投影回图像空间：
$$P_{2d}^T=K_{3\times 3}{P}_{3d}^T$$
其中$P_{2d}\in {\mathbb{R}}^{N\times 3}$。$P_{2d}$的第$i$行 为$[u_i\cdot z_i,v_i\cdot z_i,z_i]$，其中$u_i$和$v_i$为图像空间中的投影坐标，$z_i$为该点对应的深度。

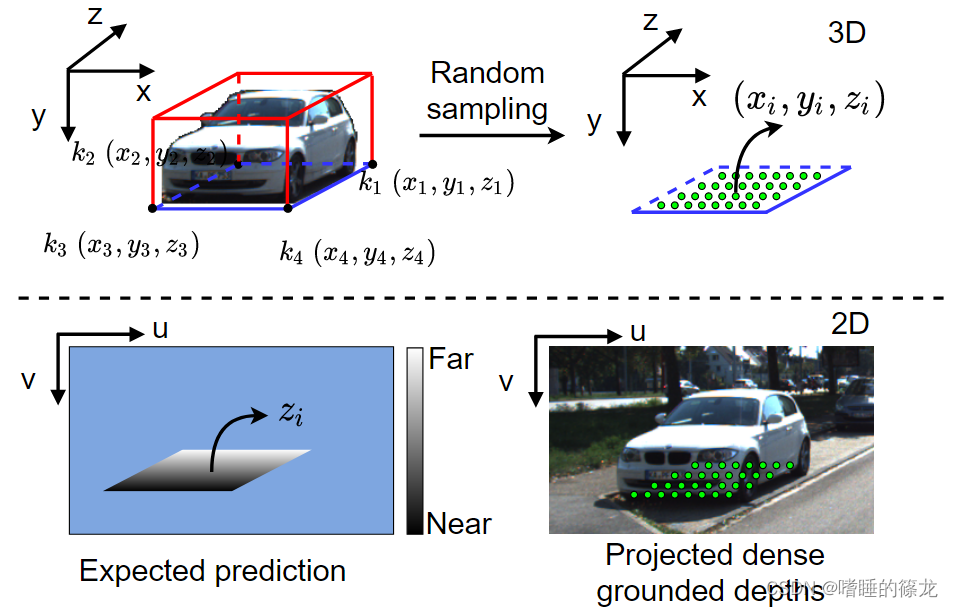
如上图所示，利用上述公式，可以得到一个密集接地的深度表示，解决了主流方法中深度监督稀疏的问题。对于不适定的2D到3D映射问题，密集的接地深度提供了地平面约束，使其成为一个适定问题，而映射的唯一解是摄像机光线与地平面的相交。此外，由于本文的公式与物体的高度没有关系，因此自然避免了不相关的相关问题。更重要的是，引入的地平面先验和密集接地深度都来自于3D边界框注释，易于访问，不需要LiDAR和深度等其他数据源

In Code

• 这部分代码的实现，在monoground\data\datasets\kitti.py文件KITTIDataset类的interp_corners3d函数中：

def interp_corners3d(self, ground_corners3d, num_interp_x=100, num_interp_y=100, sampling_method='grid',  
                     sampling_num_type='fixed', ground_corners2d=None, down_ratio=4):  
    '''  
    在目标3D框的底面上进行随机采样，生成ground先验  
    这里默认没有使用num_interp_x和y这两个参数，而是根据底面面积来进行随机采样  
    :param ground_corners3d: 目标底面的四个点的3D坐标 [4, 3]    :param num_interp_x: x方向要采样点的数目 21    :param num_interp_y: y方向要采样点的数目 21    :param sampling_method: 'random'    :param sampling_num_type: 算法使用'area'  
    :param ground_corners2d: 目标底面的四个点的2D坐标 [4, 2]    :param down_ratio: 4    :return:    '''    assert len(ground_corners3d) == 4  
    assert sampling_method in ['grid', 'random']  
    assert sampling_num_type in ['fixed', 'area']  
    if sampling_method == 'grid' and sampling_num_type == 'fixed':  
        sampling_points = np.dstack(  
            np.meshgrid(np.linspace(0, 1, num_interp_x), np.linspace(0, 1, num_interp_y))).reshape(-1, 2)  
    elif sampling_method == 'random' and sampling_num_type == 'fixed':  
        sampling_points = np.random.uniform(size=(num_interp_x * num_interp_y - 5, 2))  
        sampling_points = np.concatenate(  
            [sampling_points, np.array([[0.5, 0.5], [1., 1.], [0., 0.], [1., 0.], [0., 1.], ])], axis=0)  
  
    # 默认运行这里  
    elif sampling_method == 'random' and sampling_num_type == 'area':  
        # 鞋带公式计算不规则矩形面积  
        area = self.ploy_area(ground_corners2d[:, 0], ground_corners2d[:, 1])  
        area /= (down_ratio * down_ratio)  
        if area > self.max_area:  
            area = self.max_area  # 1600 * 928 / 32 / 32  
        if area < 5:  
            sampling_points = np.array([[0.5, 0.5], [1., 1.], [0., 0.], [1., 0.], [0., 1.], ])  
        else:  
            sampling_points = np.random.uniform(size=(ceil(area) - 5, 2))  
            sampling_points = np.concatenate(  
                [sampling_points, np.array([[0.5, 0.5], [1., 1.], [0., 0.], [1., 0.], [0., 1.], ])], axis=0)  
    else:  
        raise NotImplementedError  
    if self.only_five_gdpts:  
        sampling_points = np.array([[0.5, 0.5], [1., 1.], [0., 0.], [1., 0.], [0., 1.], ])  
  
    # num_interp_x * num_interp_y * 2  
    # u、v方向向量  
    x_vector = ground_corners3d[1] - ground_corners3d[0]  
    z_vector = ground_corners3d[3] - ground_corners3d[0]  
  
    # vector from x and z directions  
    # 最终产生地面随机采样点坐标  
    base = np.stack([x_vector, z_vector])  
    sampled_pts = sampling_points @ base + ground_corners3d[0]  
  
    return sampled_pts

• 计算底面面积：鞋带公式

def ploy_area(self, x, y):  
    '''  
    Shoelace公式，也叫高斯面积公式，是一种数学算法，可求确定区域的一个简单多边形的面积  
    '''    return 0.5 * np.abs(np.dot(x, np.roll(y, 1)) - np.dot(y, np.roll(x, 1)))

 

Pipeline

In Pape

整体网络框架基于CenterNet和MonoFlex，如下图所示

1. Backbone采用DLA34，之后分为两个branch
2. Ground Branch负责预测Grounded Depth，并且采用了Dilated Coord Conv，原因如下：

• 首先，Grunded Depth的估计涉及到视觉特征和位置特征，而普通卷积只能提供视觉特征，坐标卷积可以整合视觉和位置特征
• 其次，3D坐标$(x,y,z)$ （$z$为深度）是2D坐标的线性变换（相机投影模型）。坐标卷积可以显式地将卷积中的二维坐标串联起来，使其成为一个外部提示，从而更好地估计深度

3. 3D Branch基于MonoFlex，负责预测五类Attributes：

• Heatmap：$[C\times \frac{H}{S}\times \frac{W}{S}]$表示每个物体的中心坐标，热图越接近1，表示某类物体在该位置存在的可能性越大
• Offsets：$[22\times \frac{H}{S}\times \frac{W}{S}]$表示11个点（3个中心点+8个立方体顶点）在2D图像中的偏移，如下图所示：

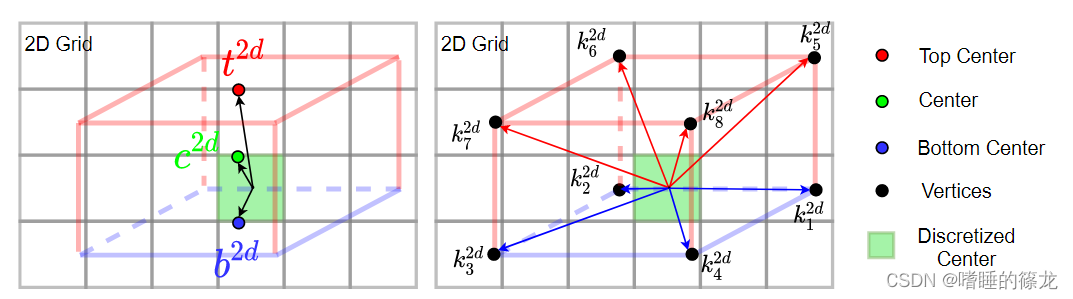
本文中定义Offsets为：
$$\begin{array}{c}{\delta }_p=\frac{p}{S}-\lfloor \frac{c^{2d}}{S}\rfloor \\ \text{ s.t. }p\in \left\{c^{2d},k_1^{2d},\cdots ,k_8^{2d},b^{2d},t^{2d}\right\}\end{array}$$
其中，$S$为Backbone的下采样率，$\lfloor \cdot \rfloor$为向下取整，假设${\delta }_p^{\ast }$为GT真值，那么Offsets的损失如下：
L offset  = ∑ p ∈ { c 2 d , k 1 2 d , ⋯   , k 8 2 d , b 2 d , t 2 d } ∣ δ p − δ p ∗ ∣ L_{\text {offset }}=\sum_{p \in\left\{c^{2 d}, k_1^{2 d}, \cdots, k_8^{2 d}, b^{2 d}, t^{2 d}\right\}}\left|\delta_p-\delta_p^*\right| Loffset ​=p∈{c2d,k12d​,⋯,k82d​,b2d,t2d}∑​∣∣​δp​−δp∗​∣∣​

• Size：$[3\times \frac{H}{S}\times \frac{W}{S}]$表示物体3D的长宽高预测值
• Orientation：$[8\times \frac{H}{S}\times \frac{W}{S}]$表示物体的偏航角（yaw），分为8部分，在KITTI数据集中，俯仰角（pitch）和旋转角（roll）均设置为0
• Direct Depth：$[1\times \frac{H}{S}\times \frac{W}{S}]$表示物体的直接深度

4. 在后处理阶段：分别预测两个Depth（Grounded Depth、Geometry Depth）

• 利用预测的Offsets，计算Geometry Depth：
  $$z=\frac{f\cdot h}{h_{2d}}$$
  其中，$f$为相机焦距，$h$物体的3D高度，$h_{2d}$为$b^{2d}-t^{2d}$，即物体的2D图像像素高度。此外，本文还通过平均对角关键点的几何深度来扩展几何深度（借鉴MonoFlex）
• 最后，通过从七个深度$z_{pred}$（1 direct depth, 3 geometry depths, 3 grounded depths)中基于不确定性的投票得到最终深度（借鉴MonoFlex）：
  $$z_{\text{final }}=\left(\sum _{i=1}^7\frac{z_{\text{pred }}^i}{{\sigma }_i}\right)/\left(\sum _{i=1}^7\frac{1}{{\sigma }_i}\right)$$
• 3 geometry depths：物体$h_{2d}$的表示有三种，即顶部中心和底部中心之间的距离，两对对角线的距离，如下图所示：

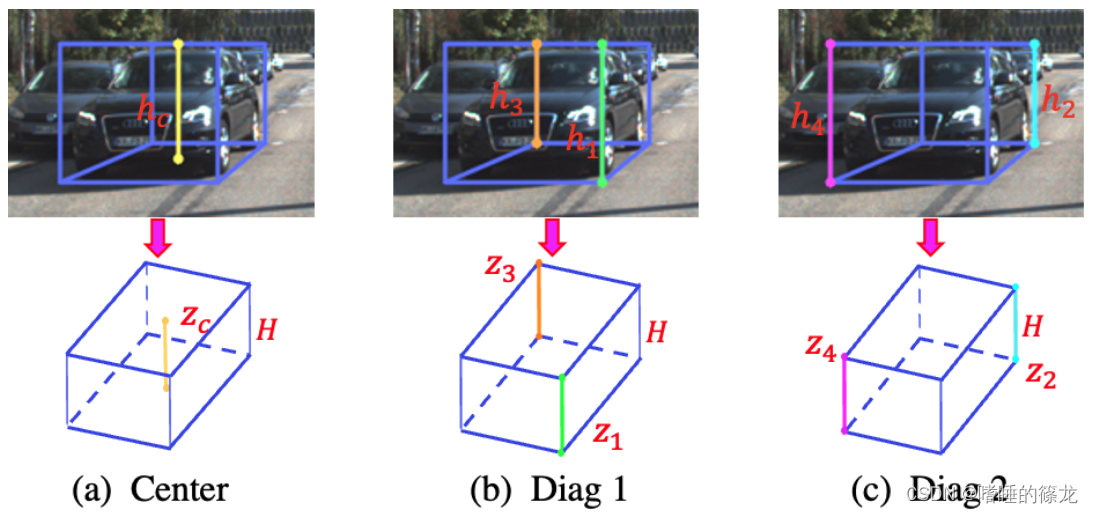
• 3 grounded depths：物体底部中心$b^{2d}$的深度、底部两对对角顶点的深度$k_1^{2d},k_3^{2d}$和$k_2^{2d},k_4^{2d}$

In Code

这里要明确两个问题：
【第一个问题】：矩形框的8个顶点坐标如何产生，以及顺序如何？

• 根据目标底面中心坐标和偏航角，我们很容易计算出$k_1$的坐标（只计算x方向和z方向即可），如下图所示：

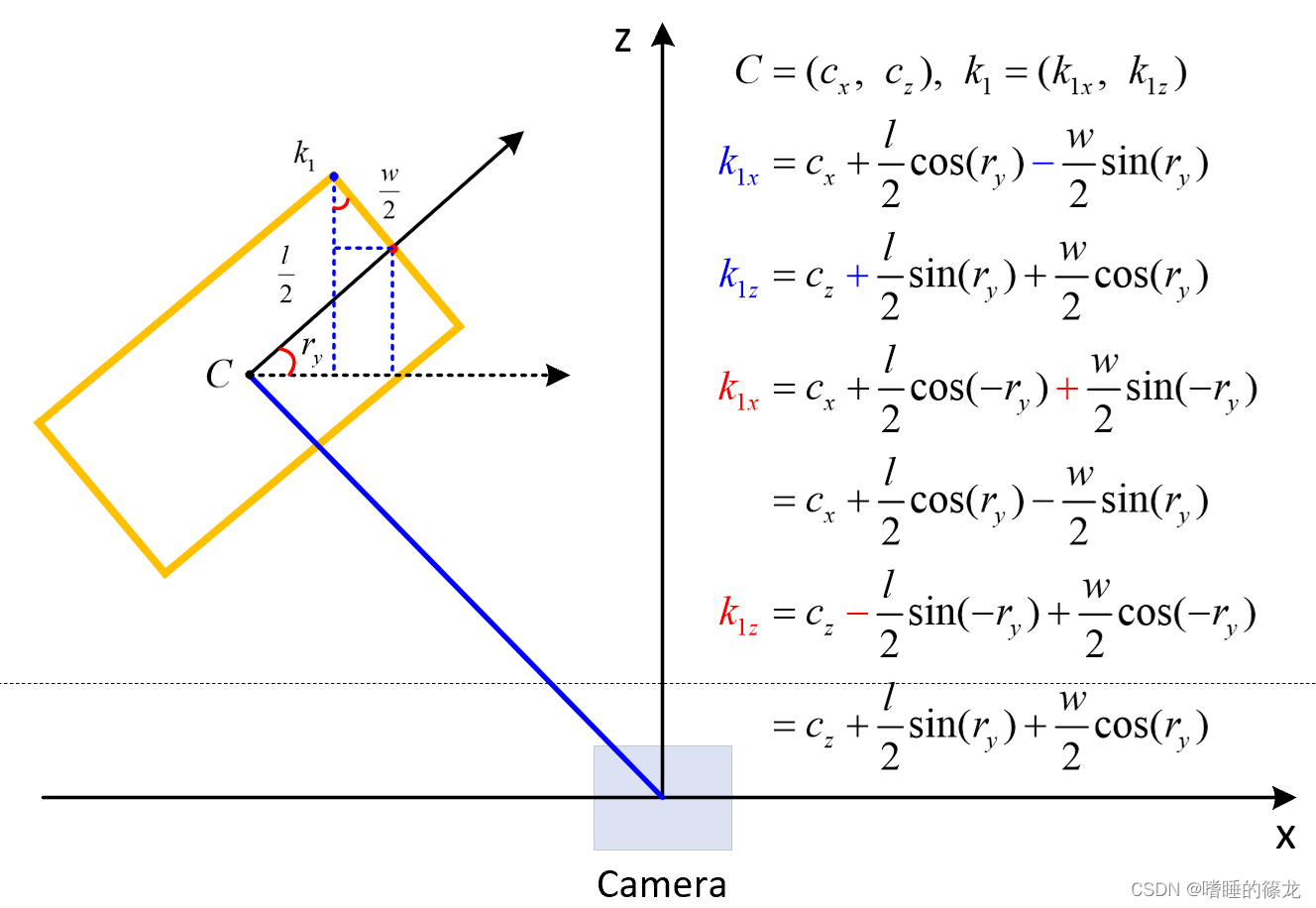
• 这样我们就得出一个转换矩阵（下图中蓝色矩阵R），但实际代码中的转换矩阵确实下图中的红色矩阵R，区别就在于，偏航角$r_y$的正负问题：在KITTI中相机坐标系下，偏航角的方向定位为：X正半轴为0°，Z正半轴为-90°
• 因此，要在$sin()$函数前面加个负号

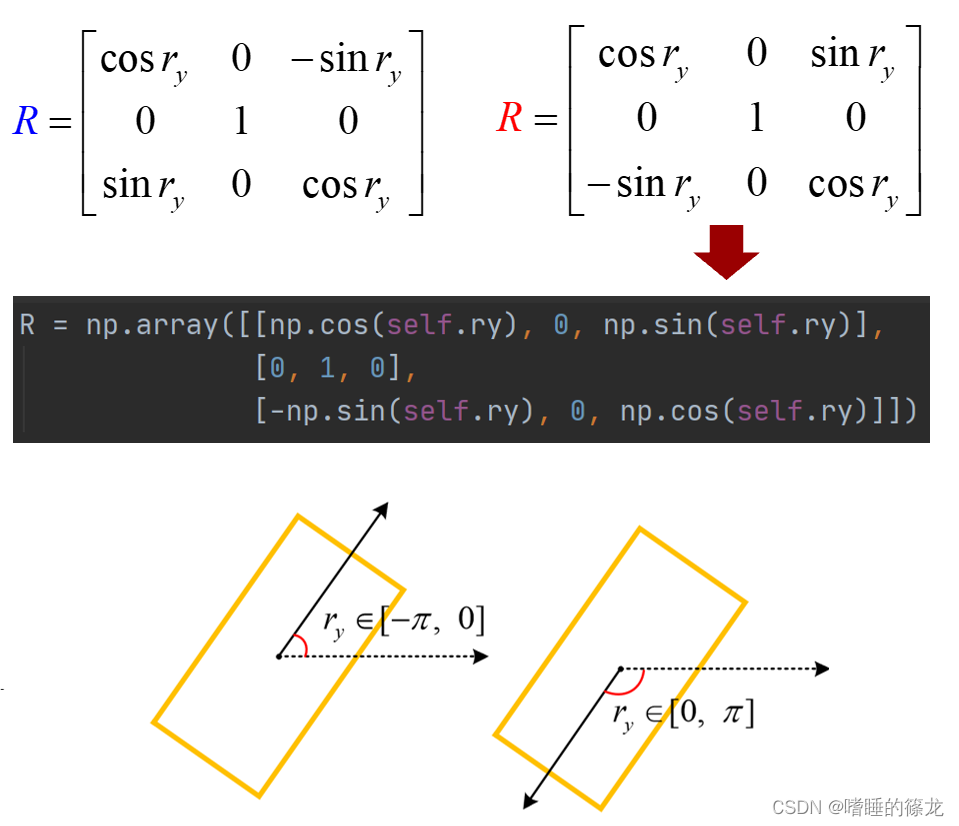
• 对应代码位于monoground\data\datasets\kitti_utils.py的generate_corners3d函数中：

def generate_corners3d(self):  
    """ 前四个为底部四个点：左前-->右前-->右后-->左后  
    generate corners3d representation for this object    self.l, self.h, self.w: 目标的3D长、高、宽  
    self.t: 目标底面的3D坐标(x, y, z)  
    self.ry: 目标的偏航角r_y
    :return corners_3d: [8, 3] corners of box3d in camera coord    """    l, h, w = self.l, self.h, self.w  
  
    # 设置8个顶点相对于底面中心点的初始偏移  
    x_corners = [l / 2, l / 2, -l / 2, -l / 2, l / 2, l / 2, -l / 2, -l / 2]  
    y_corners = [0, 0, 0, 0, -h, -h, -h, -h]  
    z_corners = [w / 2, -w / 2, -w / 2, w / 2, w / 2, -w / 2, -w / 2, w / 2]  
  
    # 定义转换矩阵  
    R = np.array([[np.cos(self.ry), 0, np.sin(self.ry)],  
                  [0, 1, 0],  
                  [-np.sin(self.ry), 0, np.cos(self.ry)]])  
  
    corners3d = np.vstack([x_corners, y_corners, z_corners])  # (3, 8)  
  
    # 8个顶点相对于底面中心点的实际偏移  
    corners3d = np.dot(R, corners3d).T  
    corners3d = corners3d + self.t  
  
    return corners3d

【第二个问题】：目标的geometry depth如何产生？

• 利用目标的2D高度和3D高度之间的相对比例来计算目标深度
  $$\begin{array}{rl}& z_l=\frac{f\times H}{h_l}\\ & h_l=h_t-h_b\end{array}$$
• 对应代码位于monoground\model\anno_encoder.py中的decode_depth_from_keypoints_batch函数中：

def decode_depth_from_keypoints_batch(self, pred_keypoints, pred_dimensions, calibs, batch_idxs=None):  
    ''' generate geometry depth  
    :param pred_keypoints: 一个batch中所有目标8个顶点，在2D图像中的坐标信息 [N, 10, 2]    :param pred_dimensions: 一个batch中所有目标的长高宽 [N, 3]    :param calibs: 校准信息，会用到u方向的焦距f_u  
    :param batch_idxs:    :return:  
    '''    # pred_keypoints: K x 10 x 2, 8 vertices, bottom center and top center  
    pred_height_3D = pred_dimensions[:, 1].clone()  
    batch_size = len(calibs)  
    if batch_size == 1:  
        batch_idxs = pred_dimensions.new_zeros(pred_dimensions.shape[0])  
  
    # 产生三个目标在2D图像上的高度：  
    # center_height: 底面中心的y坐标值-顶面中心的y坐标值 [N, ]    # corner_02_height: 目标框两条相对棱的长度[N, 2]  
    # corner_13_height: 目标框两条相对棱的长度[N, 2]  
    center_height = pred_keypoints[:, -2, 1] - pred_keypoints[:, -1, 1]  
    corner_02_height = pred_keypoints[:, [0, 2], 1] - pred_keypoints[:, [4, 6], 1]  
    corner_13_height = pred_keypoints[:, [1, 3], 1] - pred_keypoints[:, [5, 7], 1]  
  
    pred_keypoint_depths = {'center': [], 'corner_02': [], 'corner_13': []}  
  
    for idx, gt_idx in enumerate(torch.unique(batch_idxs, sorted=True).tolist()):  
        calib = calibs[idx]  
        corr_pts_idx = torch.nonzero(batch_idxs == gt_idx).squeeze(-1)  
        # 利用投影矩阵，计算三组几何深度  
        center_depth = calib.f_u * pred_height_3D[corr_pts_idx] / (  
                    F.relu(center_height[corr_pts_idx]) * self.down_ratio + self.EPS)  
        corner_02_depth = calib.f_u * pred_height_3D[corr_pts_idx].unsqueeze(-1) / (  
                    F.relu(corner_02_height[corr_pts_idx]) * self.down_ratio + self.EPS)  
        corner_13_depth = calib.f_u * pred_height_3D[corr_pts_idx].unsqueeze(-1) / (  
                    F.relu(corner_13_height[corr_pts_idx]) * self.down_ratio + self.EPS)  
  
        # 取平均  
        corner_02_depth = corner_02_depth.mean(dim=1)  
        corner_13_depth = corner_13_depth.mean(dim=1)  
  
        pred_keypoint_depths['center'].append(center_depth)  
        pred_keypoint_depths['corner_02'].append(corner_02_depth)  
        pred_keypoint_depths['corner_13'].append(corner_13_depth)  
  
    for key, depths in pred_keypoint_depths.items():  
        pred_keypoint_depths[key] = torch.clamp(torch.cat(depths), min=self.depth_range[0], max=self.depth_range[1])  
  
    pred_depths = torch.stack([depth for depth in pred_keypoint_depths.values()], dim=1)  
  
    return pred_depths

 

Depth-Align Training

网络预测的grounded points，由均匀的网格组成，处在整数位置
而由标注信息转换的投影grounded points，则是随机分散的，即非整数位置
那么二者存在不对齐的现象
那么，本文的思路是：对投影的每个随机采样grounded points，使用其周围4个网格点的深度进行损失函数的计算，来优化非整数位置的密集深度

In Paper

在得到Grounded Depth预测图后，如何训练这种预测图是一个重要的问题，因为预测的Grounded Depth与利用标签得到的投影Grounded Depth存在不对齐的问题，即投影密集接地点分布在预测图中任意位置，而预测图由均匀的网格组成。也就是说，预测图只能用于整数位置，而投影的密集接地点分布在非整数位置。为了解决这个问题，本文提出了一种深度对齐训练方法，如下图所示：

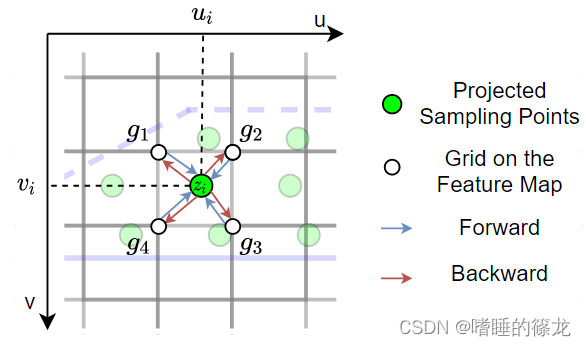
• 深度对齐训练的前向计算与双线性插值相同，设投影接地点为$(u_i,v_i)$，深度为$z_i$， { g 1 , g 2 , g 3 , g 4 } \{g_1, g_2, g_3, g_4\} {g1​,g2​,g3​,g4​}为从左上角开始顺时针环绕的四个网格点，则第$i$个点的深度预测值可以写成：
  $$\begin{array}{c}{\lambda }_1=u_i-\lfloor u_i\rfloor ,{\lambda }_2=\lceil u_i\rceil -u_i,\\ {\lambda }_3=v_i-\lfloor v_i\rfloor ,{\lambda }_4=\lceil v_i\rceil -v_i,\\ {\text{ pred }}_i={\lambda }_2{\lambda }_4{g}_1+{\lambda }_1{\lambda }_4{g}_2+{\lambda }_1{\lambda }_3{g}_3+{\lambda }_2{\lambda }_3{g}_4,\end{array}$$
• 那么接地点的总深度损失为：
  $$L_{da}=\sum _{i=1}^N\left|z_i-{\mathrm{pred}}_i\right|$$
• 这样，我们可以直接优化非整数位置的密集深度，反向传播是根据双线性插值的权重将梯度传递给周围的网格点
• 【疑问1】：为什么要用投影点周围的四个网格点来进行双线性插值呢？
  • 【解答1】： 计算该非整数位置的深度值和深度不确定值，便于和GT值进行loss计算
• 【疑问2】：$g$是什么意思呢？每个网格点的深度值？
  • 【解答2】 ：深度值和深度不确定值

In Code

• 对应代码位置：monoground\model\layers\utils.py中的soft_get函数

def soft_get(reg, pts, force_get=False, force_get_uncertainty=False):  
    '''  
    深度对齐，考虑到随机采样的底面真值点的坐标不是整数  
    因此无法直接与网络预测产生的网格点的深度进行损失函数的计算    :param reg: 网络预测的ground深度值  
    :param pts: 随机采样的底面真值坐标  
    :return:  
        rop: 随机采样底面真值点，对应于网络输出预测特征图的值(深度值和深度不确定性值)  
        valid_idx: 随机采样地面真值点的有效索引  
    '''    pts_x = pts[:, 0]  
    pts_y = pts[:, 1]  
  
    h, w = reg.shape[-2], reg.shape[-1]  
    # if force_get:  
    #     pts_x = pts_x.clamp(0, w-1)    #     pts_y = pts_y.clamp(0, h-1)  
    # 获取随机采样点周围的四个网格点坐标  
    pts_x_low = pts_x.floor().long()  
    pts_x_high = pts_x.ceil().long()  
  
    pts_y_low = pts_y.floor().long()  
    pts_y_high = pts_y.ceil().long()  
  
    # 是否超出特征图  
    valid_idx = (pts_y_low >= 0) & (pts_y_high < h) & (pts_x_low >= 0) & (pts_x_high < w)  
  
    # 四个网格点的有效坐标  
    pts_x_low_valid = pts_x_low[valid_idx]  
    pts_x_high_valid = pts_x_high[valid_idx]  
    pts_y_low_valid = pts_y_low[valid_idx]  
    pts_y_high_valid = pts_y_high[valid_idx]  
  
    # 随机采样点的有效坐标  
    pts_x = pts_x[valid_idx]  
    pts_y = pts_y[valid_idx]  
  
    # 四个有效网格点的深度值  
    rop_lt = reg[..., pts_y_low_valid, pts_x_low_valid]  
    rop_rt = reg[..., pts_y_low_valid, pts_x_high_valid]  
    rop_ld = reg[..., pts_y_high_valid, pts_x_low_valid]  
    rop_rd = reg[..., pts_y_high_valid, pts_x_high_valid]  
  
    rop_t = (1 - pts_x + pts_x_low_valid) * rop_lt + (1 - pts_x_high_valid + pts_x) * rop_rt  
    rop_d = (1 - pts_x + pts_x_low_valid) * rop_ld + (1 - pts_x_high_valid + pts_x) * rop_rd  
  
    rop = (1 - pts_y + pts_y_low_valid) * rop_t + (1 - pts_y_high_valid + pts_y) * rop_d  
  
    # False  
    # torch.all(valid_idx) 全部为True时返回True  
    if force_get and not torch.all(valid_idx):  
        shape = list(rop.shape)  
        shape[-1] = len(valid_idx)  
        rop_force = torch.zeros(*shape, dtype=rop.dtype, device=rop.device)  
        rop_force[..., valid_idx] = rop  
  
        pts_invalid = pts[~valid_idx]  
  
        grid = generate_grid(w, h).to(pts_invalid.device)  
        reg_invalid_all = []  
        for pts_in in pts_invalid:  
            diff = (pts_in - grid)  
            dis = diff[:, 0] ** 2 + diff[:, 1] ** 2  
            closest_idx = dis.argmin()  
  
            reg_invalid_all.append(reg[..., grid[closest_idx, 1].long(), grid[closest_idx, 0].long()])  
        reg_invalid_all = torch.stack(reg_invalid_all, dim=-1)  
        rop_force[..., ~valid_idx] = reg_invalid_all.detach()  
        if force_get_uncertainty:  
            # import pdb; pdb.set_trace()  
            # assert rop_force.shape[0] == 2            if rop_force.shape[0] == 2:  
                rop_force[1, ~valid_idx] = 30  
            elif rop_force.shape[0] == 6:  
                rop_force[1, ~valid_idx] = 30  
                rop_force[3, ~valid_idx] = 30  
                rop_force[5, ~valid_idx] = 30  
            else:  
                raise NotImplementedError  
        return rop_force, valid_idx  
  
    return rop, valid_idx

 

Two-stage Depth Inference

目前理解：Ground Branch就是用来预测接地点，每一个接地点的深度都是唯一的，并且理论上接地点的深度，等于该点向上延伸中所有点的深度值，例如：底部中心点的深度=物体中心点的深度=顶部中心点的深度。那么，就可以利用Ground Branch来获得接地点的深度值，来辅助最终深度的生成（在Loss计算中加入地面随机采样点的预测）
其中两阶段的含义：在深度估计之前使用3D分支的回归结果

在CenterNet-Style的推理中，对象由特征图上的粗网格点表示，所有其他属性都由点上的特征一次性预测，称之为单阶段推理。但是粗网格点只能反映物体的粗位置，这就是为什么我们需要进一步回归GT位置和粗网格位置之间的差异
在密训练的接地深度图的帮助下，我们使用回归的细粒度位置代替粗糙的网格位置，可以实现比原来的CenterNet式深度推断更精确的深度估计，二者的区别如下图所示：

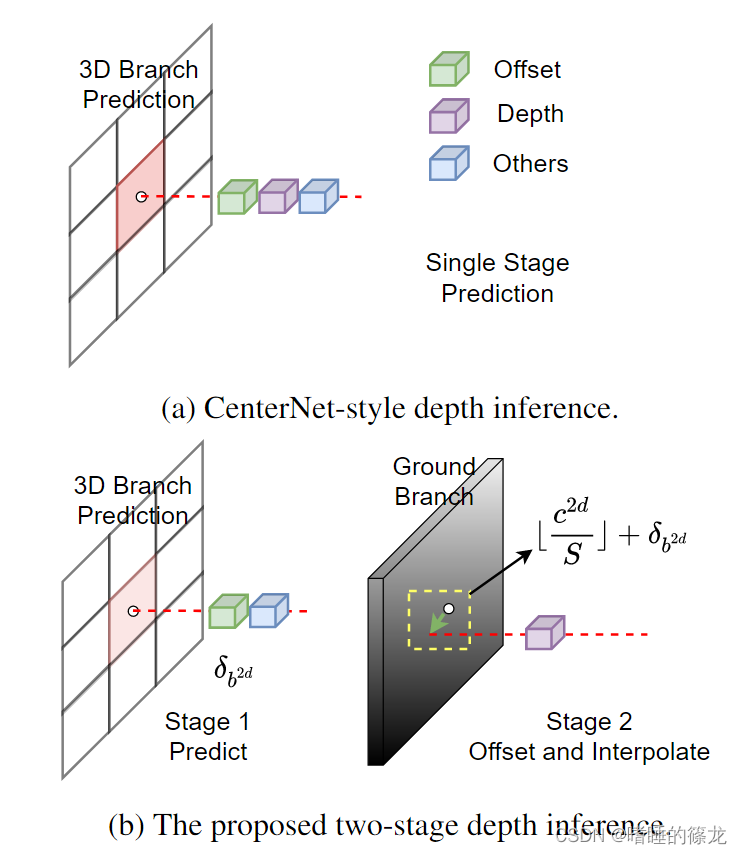
• 第一个Ground Depth：假设$\lfloor c^{2\mathbf{d}}/S\rfloor$是热图预测的中心。我们首先对中心进行回归偏移，得到物体底部中心点的精细位置$b^{2\mathbf{d}}/S=\lfloor c^{2\mathbf{d}}/S\rfloor +{\delta }_{b^{2\mathbf{d}}}$，然后对地面支路预测采用深度对齐的前向计算公式进行插值，得到精确深度。由于$b^{2\mathbf{d}}$为物体的底部中心，因此$b^{2\mathbf{d}}$的接地深度与$c^{2\mathbf{d}}$的深度完全相同，即物体的中心深度
• 第二、三个Ground Depth：利用物体底部框的四个角点，根据三维几何结构，中心深度等于对角线关键点的平均深度。这样，可以利用得到的对角线结果求平均值，从关键点$k_1^{2d},k_3^{2d}和k_2^{2d},k_4^{2d}$得到另外两个深度估计