文章目录
一、理论基础
1、基本布谷鸟算法
请参考这里。
2、多阶段动态扰动和动态惯性权重的布谷鸟优化算法(MACS)
(1)多阶段动态扰动策略
在布谷鸟算法的全局搜索阶段,所有鸟窝位置都朝着同一全局最优位置靠近,致使布谷鸟算法很容易陷入局部最优,导致算法在处理复杂多峰函数时,收敛精度低,收敛过早等缺点表现得尤为明显。针对这个问题,本文提出了一种多阶段动态扰动策略,对布谷鸟算法的最优鸟窝位置迚行分阶段的动态扰动,更新最优鸟窝位置。即对全局最优鸟窝位置根据方差可调的正态随机分布迚行扰动,从而得到新的全局最优鸟窝位置
X
N
e
w
b
e
s
t
X_{Newbest}
XNewbest,更新公式如(1)所示:
X
N
e
w
b
e
s
t
=
N
(
X
b
e
s
t
,
σ
)
(1)
X_{Newbest}=N(X_{best},\sigma)\tag{1}
XNewbest=N(Xbest,σ)(1)其中,
σ
\sigma
σ表示相对于
X
b
e
s
t
X_{best}
Xbest的不确定度,是关于迭代次数
t
t
t的非增函数,其更新公式如下:
σ
=
{
σ
1
,
t
<
α
1
T
σ
1
−
(
σ
1
−
σ
2
)
(
t
−
α
1
T
)
(
α
2
T
−
α
1
T
)
,
α
1
T
<
t
<
α
2
T
σ
2
,
t
>
α
2
T
(2)
\sigma=\begin{dcases}\sigma_1\quad \quad \quad \quad \quad\quad \quad \quad\quad \,\,\,,t<\alpha_1T\\\sigma_1-\frac{(\sigma_1-\sigma_2)(t-\alpha_1T)}{(\alpha_2T-\alpha_1T)},\alpha_1T<t<\alpha_2T\\\sigma_2\quad \quad \quad \quad \quad\quad \quad \quad\quad \,\,\,,t>\alpha_2T\end{dcases}\tag{2}
σ=⎩⎪⎪⎨⎪⎪⎧σ1,t<α1Tσ1−(α2T−α1T)(σ1−σ2)(t−α1T),α1T<t<α2Tσ2,t>α2T(2)其中,
σ
\sigma
σ表示对原最优鸟窝位置正态扰动的半径参数,且
σ
1
<
σ
2
\sigma_1<\sigma_2
σ1<σ2,本文取
σ
1
=
0.9
,
σ
2
=
0.000001
\sigma_1=0.9,\sigma_2=0.000001
σ1=0.9,σ2=0.000001;
α
1
,
α
2
\alpha_1,\alpha_2
α1,α2是半径变化的控制参数,且
α
1
<
α
2
\alpha_1<\alpha_2
α1<α2,本文取
α
1
=
0.4
,
α
2
=
0.4
\alpha_1=0.4,\alpha_2=0.4
α1=0.4,α2=0.4,
t
t
t是当前迭代次数,
T
T
T是最大迭代次数。其扰动半径
σ
\sigma
σ变化图如下:
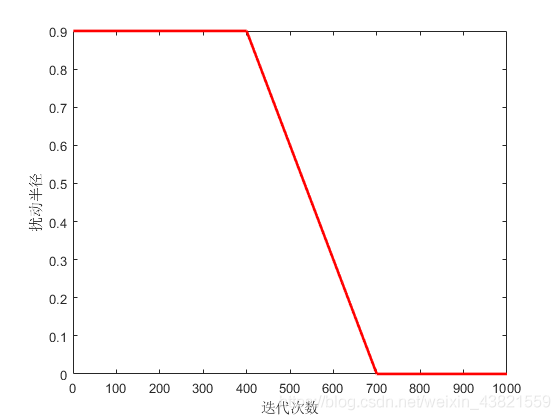
由图1可以看出,扰动半径 σ \sigma σ是一个分为三阶段的动态变化数值。在算法迭代前期以固定较大的半径对布谷鸟算法的全局最优鸟窝位置迚行扰动,得到新的变化较大的最优鸟窝位置,使全体鸟窝在朝着新的最优鸟窝位置靠近时,更具有广泛性和多样性,帮助算法在迭代前期更大范围内的去寻找全局最优,避免算法朝着固定最优鸟窝位置靠近,而在迭代前期就陷入局部最优的情况。当在迭代中期,算法在逐步缩小范围寻找全局最优时,本文也以线性递减的方式逐步降低对最优鸟窝位置的扰动半径,使全体鸟窝位置逐步稳定的向全局最优靠近。而在最后迭代后期,算法已经非常靠近寻求出全局最优解时,本文以固定非常微小的扰动半径对当前最优鸟窝位置迚行扰动,不再大范围波动当前最优位置,使算法小范围内精细搜索出全局最优解。
(2)动态惯性权重
动态惯性权重改迚策略是一种能够动态平衡全局搜索和局部搜索的改进机制,能够提高算法的搜索速度和收敛精度。本文在上一代鸟窝位置处引入自适应动态惯性权重对布谷鸟算法的偏好随机游动环节进行改进。改进后的布谷鸟偏好随机游动环节公式如(3)所示:
x
i
t
+
1
=
x
i
t
+
γ
⋅
(
x
j
t
−
x
k
t
)
(3)
x_i^{t+1}=x_i^t+\gamma\cdot(x_j^t-x_k^t)\tag{3}
xit+1=xit+γ⋅(xjt−xkt)(3)其中,动态惯性权重
w
w
w公式如(4)所示:
w
=
sin
(
π
t
2
T
+
π
)
+
1
(4)
w=\sin\left(\frac{\pi t}{2T}+\pi\right)+1\tag{4}
w=sin(2Tπt+π)+1(4)其中,
t
t
t为当前迭代次数,
T
T
T是最大迭代次数,
w
w
w变化见图2。
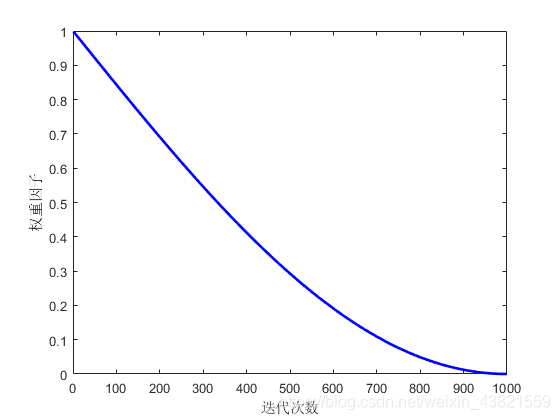
通过图2可以看出, w w w为 ( 0 , 1 ) (0,1) (0,1)之间随迭代次数非线性递减的动态惯性权重,随着迭代过程的进行,惯性权重 w w w逐步减小。在迭代前期,给上一代鸟窝位置赋予相对大的系数,使上一代鸟窝具有更大的作用能力与范围,帮助布谷鸟算法在前期扩大搜索空间, 广泛寻找全局最优解。随着算法迭代过程的进行,惯性权重系数逐渐减小,直至到迭代后期,算法接近最优解时,对上一代鸟窝位置采用相对较小的惯性权重系数,有效的削弱了上一代鸟窝的保留信息,帮助布谷鸟算法有效跳出局部最优,使布谷鸟个体具有更好的局部寻优能力。本文通过动态惯性权重系数的引入,灵活处理上一代鸟窝的位置信息,提高了算法的局部寻优能力。
(3)自适应切换概率
自适应概率
p
p
p是布谷鸟算法的重要参数,当
p
p
p较小时,增加了全局的多样性,提高全局搜索能力,当
p
p
p较大时,增加局部搜索能力,提高了算法精度和效率。所以动态概率
p
p
p是一种综合提高算法性能的优化改进策略。本文提出的动态概率公式如下式(5)所示:
p
=
0.25
−
0.1
∗
(
T
−
t
)
/
T
(5)
p=0.25-0.1*(T-t)/T\tag{5}
p=0.25−0.1∗(T−t)/T(5)
p
p
p的变化见图3。
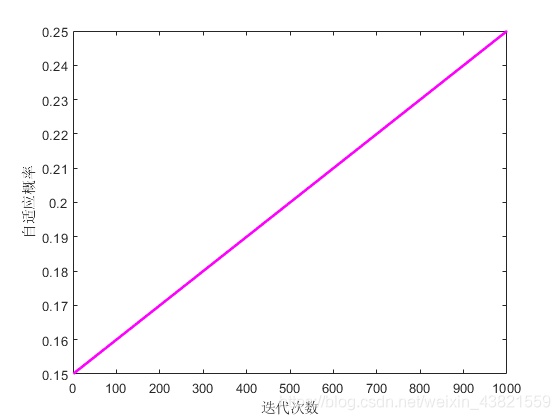
由图3可以看出,本文提出的概率 p p p是一个随迭代过程进行而自适应增大的动态切换概率。在算法迭代前期,以较小的概率 p p p来控制全局搜索和局部搜索的切换,在这个阶段由于概率 p p p较小,所以帮助算法在迭代前期多迚行全局搜索,大范围寻找全局最优解,增加了算法的全局多样性,提高了算法的全局搜索能力。随着迭代过程的进行,概率 p p p不断增大,直至在迭代后期,概率 p p p相对较大,帮助算法在迭代后期已经靠近全局最优解时,多进行局部精细搜索,提高算法的运算精度和搜索效率。通过将布谷鸟算法的固定概率替换成自适应切换概率,将概率 p p p与迭代过程动态联系在一起,帮助算法灵活平衡了全局搜索能力和局部搜索能力,提高算法性能。
二、MACS算法流程
MACS具体执行步骤如下:
Step 1:设置布谷鸟算法初始参数,鸟的个数
N
N
N,解的维数
n
n
n,最大迭代次数
T
T
T,依照(5)式设置发现概率
p
p
p,搜索上下界。随机初始化鸟窝位置
X
0
=
(
x
1
0
,
x
2
0
,
⋯
,
x
N
0
)
X_0=(x_1^0,x_2^0,\cdots,x_N^0)
X0=(x10,x20,⋯,xN0),计算每个鸟窝的适应度
f
i
=
f
(
x
i
)
,
i
=
1
,
2
,
⋯
,
N
f_i=f(x_i),i=1,2,\cdots,N
fi=f(xi),i=1,2,⋯,N;
Step 2:按照基本布谷鸟算法更新鸟窝位置
X
t
=
(
x
1
t
,
x
2
t
,
⋯
,
x
N
t
)
X_t=(x_1^t,x_2^t,\cdots,x_N^t)
Xt=(x1t,x2t,⋯,xNt),进行全局搜索,计算更新解的适应度,如果更新解的适应度值更小就替换旧的解得到一组较优的鸟窝位置
G
t
=
(
x
1
t
,
x
2
t
,
⋯
,
x
N
t
)
G_t=(x_1^t,x_2^t,\cdots,x_N^t)
Gt=(x1t,x2t,⋯,xNt);
Step 3:对Step 2产生的全局最优解
X
b
e
s
t
(
0
)
X_{best}^{(0)}
Xbest(0)按照公式(1)(2)进行多阶段动态扰动,更新鸟窝位置
B
t
=
(
x
1
t
,
x
2
t
,
⋯
,
x
N
t
)
B_t=(x_1^t,x_2^t,\cdots,x_N^t)
Bt=(x1t,x2t,⋯,xNt)和全局最优解
X
b
e
s
t
(
t
)
X_{best}^{(t)}
Xbest(t);
Step 4:按照式(5)的动态发现概率p淘汰部分解,并用改进后的偏好随机游动公式(3)产生于淘汰数量相同的新解,计算新解的适应度值,与
B
t
=
(
x
1
t
,
x
2
t
,
⋯
,
x
N
t
)
B_t=(x_1^t,x_2^t,\cdots,x_N^t)
Bt=(x1t,x2t,⋯,xNt)的适应度值进行比较,用好的适应度值的位置替代适应度值差的位置,得到一组较优的鸟窝位置
A
t
=
(
x
1
t
,
x
2
t
,
⋯
,
x
N
t
)
A_t=(x_1^t,x_2^t,\cdots,x_N^t)
At=(x1t,x2t,⋯,xNt);
Step 5:计算各个鸟窝的适应度值,找出
A
t
=
(
x
1
t
,
x
2
t
,
⋯
,
x
N
t
)
A_t=(x_1^t,x_2^t,\cdots,x_N^t)
At=(x1t,x2t,⋯,xNt)中最好的鸟窝位置
X
b
e
s
t
(
t
)
X_{best}^{(t)}
Xbest(t)和最优的适应度值
f
m
i
n
f_{min}
fmin;
Step 6:判断算法的终止条件,若满足,就输出当前最优值
f
m
i
n
f_{min}
fmin;若不满足,就重复Step 2~Step 6。
三、仿真实验与分析
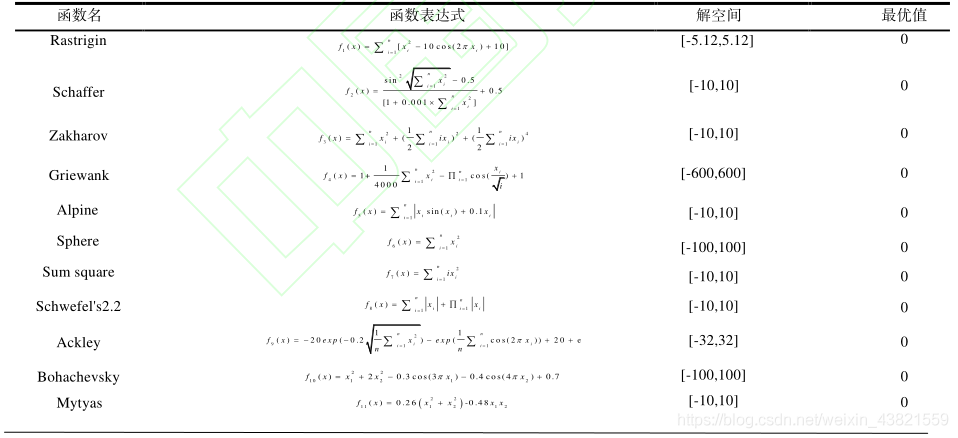
为了证明MACS算法的寻优性能,本文选取了 11个不同难度的函数,其中涵盖简单低峰函数和复杂多峰函数、高维函数和低维函数,函数设置见表1。分别对MACS算法的收敛速度、收敛精度进行测试。同时与ASCSA算法、CS算法、FPA算法、BA算法,四种算法进行对比分析。
1、测试函数
2、测试环境及算法参数
实验环境如下:CPU为i7-7700U@3.6GHz,运行内存8G,操作系统Windows10,编程环境MatlabR2018a。四种算法设置参数见文献[1]表2所示。
3、算法求解精度比较分析
分别对测试函数在10维变量下(表1最后两个测试函数为2维)进行比较分析。独立运算30次,每次运算法迭代1000次。
图4~14分别为11个测试函数的收敛曲线对比图。

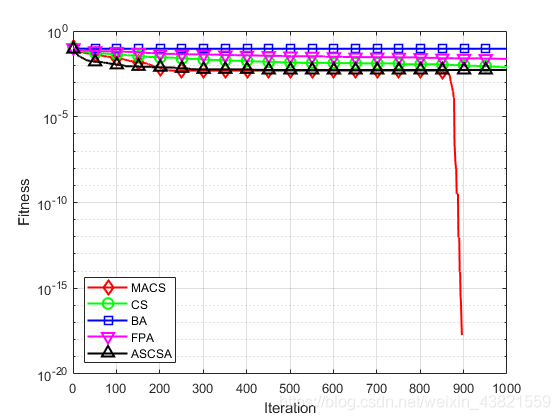
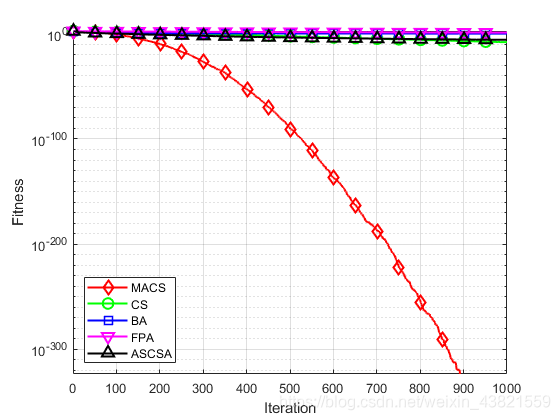

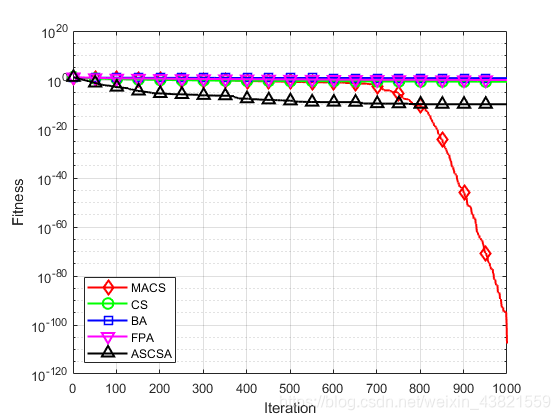
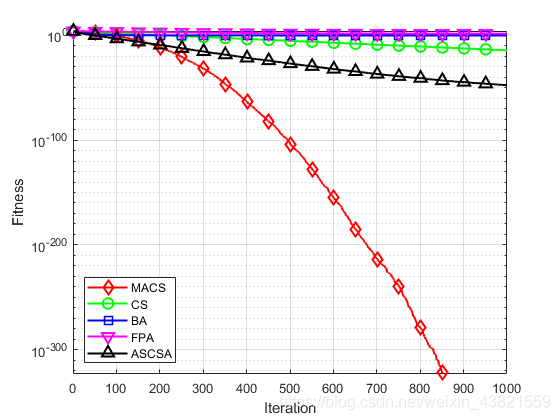
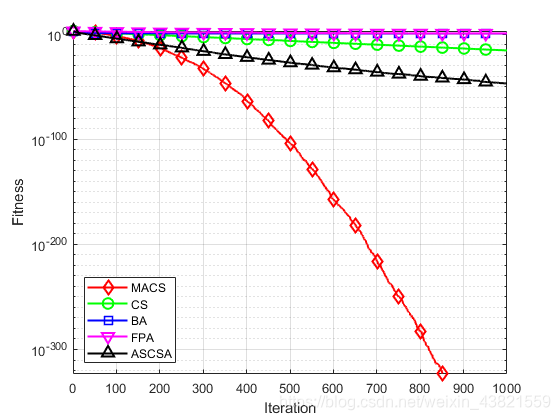
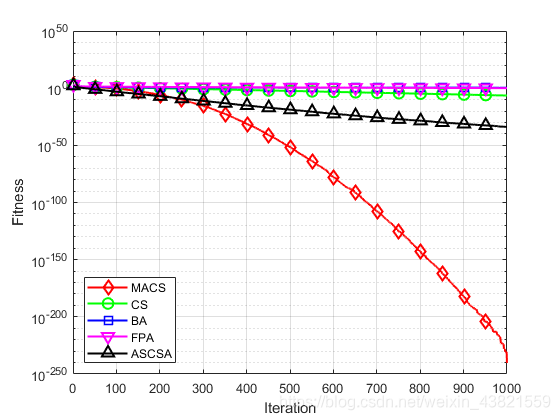

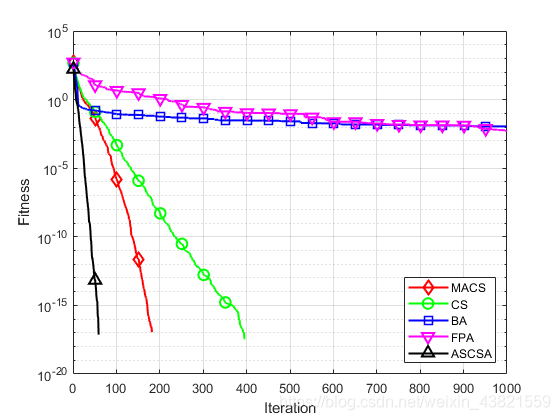
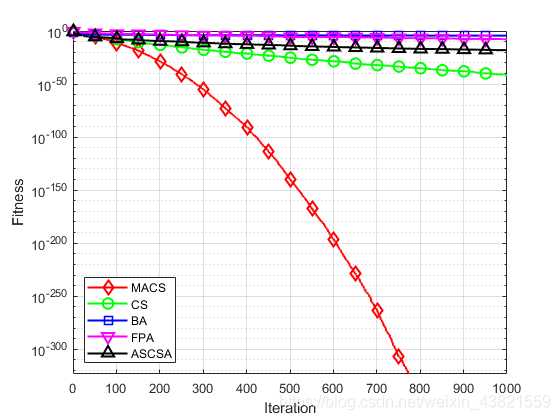
各个测试函数的最大值、最小值、平均值及标准差显示如下:
函数:Rastrigin
MACS:最大值: 0,最小值:0,平均值:0,标准差:0
CS:最大值: 9.9567,最小值:2.5658,平均值:6.2934,标准差:1.8954
BA:最大值: 101.0944,最小值:36.5992,平均值:60.8459,标准差:12.157
FPA:最大值: 74.3119,最小值:13.1144,平均值:25.0745,标准差:11.4836
ASCSA:最大值: 6.9647,最小值:0,平均值:1.7909,标准差:1.5764
函数:Schaffer
MACS:最大值: 0,最小值:0,平均值:0,标准差:0
CS:最大值: 0.018981,最小值:0.0048842,平均值:0.0077071,标准差:0.0057332
BA:最大值: 0.13104,最小值:0.040773,平均值:0.092242,标准差:0.026346
FPA:最大值: 0.068163,最小值:0.0048843,平均值:0.023835,标准差:0.015379
ASCSA:最大值: 0.018981,最小值:0.0048842,平均值:0.0053541,标准差:0.0025737
函数:Zakharov
MACS:最大值: 0,最小值:0,平均值:0,标准差:0
CS:最大值: 4.4718e-08,最小值:4.3195e-10,平均值:8.7354e-09,标准差:9.6517e-09
BA:最大值: 1.7886,最小值:0.54846,平均值:1.1596,标准差:0.32446
FPA:最大值: 76.8971,最小值:0.43134,平均值:9.7848,标准差:20.0284
ASCSA:最大值: 9.2441e-06,最小值:7.1027e-09,平均值:1.5259e-06,标准差:2.3697e-06
函数:Griewank
MACS:最大值: 0,最小值:0,平均值:0,标准差:0
CS:最大值: 0.10043,最小值:0.0029428,平均值:0.044553,标准差:0.019258
BA:最大值: 48.4967,最小值:2.5579,平均值:16.9508,标准差:11.8228
FPA:最大值: 7.7118,最小值:0.07165,平均值:0.5498,标准差:1.3797
ASCSA:最大值: 0.14522,最小值:0,平均值:0.057408,标准差:0.029417
函数:Alpine
MACS:最大值: 8.8044e-107,最小值:0,平均值:2.9417e-108,标准差:1.6073e-107
CS:最大值: 0.48185,最小值:0.019828,平均值:0.20014,标准差:0.10758
BA:最大值: 11.2913,最小值:2.6162,平均值:5.6295,标准差:2.1361
FPA:最大值: 2.7789,最小值:0.16801,平均值:1.0289,标准差:0.62061
ASCSA:最大值: 3.7583e-09,最小值:5.1027e-100,平均值:1.2528e-10,标准差:6.8618e-10
函数:Sphere
MACS:最大值: 0,最小值:0,平均值:0,标准差:0
CS:最大值: 2.2253e-14,最小值:3.4939e-16,平均值:5.5236e-15,标准差:5.1063e-15
BA:最大值: 1.0794,最小值:0.35263,平均值:0.6879,标准差:0.17256
FPA:最大值: 1309.1841,最小值:0.00023021,平均值:46.264,标准差:238.8361
ASCSA:最大值: 3.2978e-47,最小值:2.6094e-53,平均值:1.9537e-48,标准差:6.1329e-48
函数:Sum square
MACS:最大值: 0,最小值:0,平均值:0,标准差:0
CS:最大值: 1.3035e-15,最小值:3.6084e-17,平均值:2.6529e-16,标准差:3.1064e-16
BA:最大值: 4.9461,最小值:0.76171,平均值:3.1578,标准差:1.0511
FPA:最大值: 74.0895,最小值:9.9428e-06,平均值:3.6905,标准差:14.5081
ASCSA:最大值: 3.086e-46,最小值:2.124e-55,平均值:1.0436e-47,标准差:5.6317e-47
函数:Schwefel's2.2
MACS:最大值: 1.6086e-239,最小值:0,平均值:5.5207e-241,标准差:0
CS:最大值: 7.7784e-07,最小值:1.5394e-07,平均值:3.496e-07,标准差:1.6196e-07
BA:最大值: 3.2953,最小值:1.288,平均值:2.1021,标准差:0.38809
FPA:最大值: 18.8002,最小值:0.011049,平均值:1.0958,标准差:3.4672
ASCSA:最大值: 1.0623e-33,最小值:1.2555e-37,平均值:1.2372e-34,标准差:2.7531e-34
函数:Ackley
MACS:最大值: 4.5387e-228,最小值:0,平均值:1.5129e-229,标准差:0
CS:最大值: 8.7495e-07,最小值:6.9893e-08,平均值:3.8391e-07,标准差:1.9397e-07
BA:最大值: 52.2304,最小值:1.3028,平均值:7.784,标准差:14.8012
FPA:最大值: 5.1372,最小值:0.032912,平均值:0.73158,标准差:1.0635
ASCSA:最大值: 6.0533e-34,最小值:9.3829e-38,平均值:3.9459e-35,标准差:1.1496e-34
函数:Bohachevsky
MACS:最大值: 0,最小值:0,平均值:0,标准差:0
CS:最大值: 0,最小值:0,平均值:0,标准差:0
BA:最大值: 0.03962,最小值:0.00054011,平均值:0.011138,标准差:0.011178
FPA:最大值: 0.14183,最小值:0,平均值:0.0047722,标准差:0.025886
ASCSA:最大值: 0,最小值:0,平均值:0,标准差:0
函数:Mytyas
MACS:最大值: 0,最小值:0,平均值:0,标准差:0
CS:最大值: 1.8917e-41,最小值:6.4787e-48,平均值:1.6967e-42,标准差:4.1291e-42
BA:最大值: 0.00013716,最小值:2.9585e-06,平均值:3.9984e-05,标准差:3.529e-05
FPA:最大值: 3.2245e-07,最小值:1.7098e-24,平均值:1.7781e-08,标准差:6.8479e-08
ASCSA:最大值: 2.6252e-17,最小值:3.6965e-105,平均值:8.7614e-19,标准差:4.7927e-18
通过对这5种算法的收敛曲线进行比较分析,可以看出,无论是单峰函数还是复杂多峰函数,无论是高维函数还是低维函数,无论是寻优能力还是寻优精度上,MACS算法的寻优表现都优于其他四个算法,表现出良好的性能。
四、参考文献
[1] 张珍珍, 贺兴时, 于青林, 等. 多阶段动态扰动和动态惯性权重的布谷鸟算法[J]. 计算机工程与应用, 2022, 58(1): 79-88.
[2] 李荣雨, 戴睿闻. 自适应步长布谷鸟搜索算法[J]. 计算机科学, 2017, 44(5): 235-240.

























 68
68











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










