Programming Differential Privacy第八章

LOCAL SENSITIVITY局部敏感度

目标：
•定义局部敏感性并解释其与全局敏感性的区别
•描述当地敏感性如何泄漏数据信息
•使用建议的测试版本安全地应用局部敏感性
•描述平稳的敏感性框架
•使用样本和聚合框架回答具有任意敏感性的查询
到目前为止，我们只看到了一种衡量敏感性的方法：全球敏感性。我们对全球敏感性的定义考虑了
两个相邻的数据集。这似乎很悲观，因为我们将在实际数据集-我们不应该考虑该数据集的邻居吗？
这就是局部敏感性背后的直觉[8]：将两个数据集中的一个固定为被查询的实际数据集，并考虑其所有邻居。形式上，函数的局部敏感性𝑓 ∶ 𝒟 → ℝ 在𝑥 ∶ 𝒟 定义为：

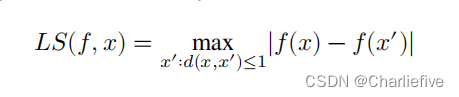
注意，局部敏感性是包含查询的函数(𝑓) 和实际数据集(𝑥)。与全球不同敏感度，我们不能在不考虑本地函数的数据集的情况下讨论函数的局部敏感度。两者缺一不可

8.1 Local Sensitivity of the Mean平均值的局部敏感性

局部灵敏度允许我们对某些函数的灵敏度设置有限的界限，而这些函数的全局灵敏度很难限制。平均函数就是一个例子。到目前为止，我们已经通过将查询划分为两个查询来计算差异私有方法：一个差异私有和（分子）和一个差异私有计数（分母）。通过序列组合和后处理，这两个结果的商满足差分隐私。
我们为什么要这样做？因为当向数据集添加行或从数据集中删除行时，平均查询的输出量可能会发生变化，这取决于数据集的大小。如果我们想绑定一个平均查询的全局敏感性，我们就必须假设最坏的情况：一个大小为1的数据集。在这种情况下，如果数据属性值位于上界和下界𝑢和𝑙之间，则均值的全局灵敏度仅为|𝑢−𝑙|。对于大型数据集，这是非常悲观的，而“噪声和超过噪声计数”的方法要好得多。
而局部敏感性的情况则有所不同。在最坏的情况下，我们可以向包含最大值（𝑢）的数据集添加一个新行。让𝑛=|𝑥|（即数据集的大小）。我们从平均值的值开始：

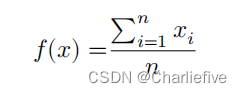
添加一行以后
这个局部灵敏度度量是根据实际数据集的大小来定义的，这在全局灵敏度下是不可能的。

8.2 Achieving Differential Privacy via Local Sensitivity?通过本地敏感度实现不同的隐私权？

不能使用局部敏感性直接实现差分隐私：如果分析人员知道在特定数据集上的查询的局部敏感性，那么分析人员就可以推断出关于该数据集的一些信息。会造成隐私的泄露。因此不能直接用局部敏感度考虑差分隐私。例如，考虑上面定义的平均值的局部灵敏度的界。如果我们知道一个特定𝑥的局部灵敏度，我们就可以在没有噪声的情况下推断出𝑥的确切大小：

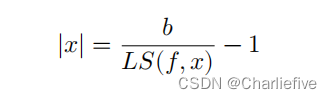
此外，对分析师对当地的敏感性保密也没有帮助。可以从几个查询回答中确定噪声的规模，分析人员可以使用这个值来推断局部敏感度。（可以用噪声规模推断局部敏感度）差异隐私是为了保护𝑓（𝑥）的输出，而不是在其定义中使用的灵敏度度量。

%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
import pandas as pd
import numpy as np

adult = pd.read_csv("adult_with_pii.csv")
def laplace_mech(v, sensitivity, epsilon):
    return v + np.random.laplace(loc=0, scale=sensitivity / epsilon)
def pct_error(orig, priv):
    return np.abs(orig - priv)/orig * 100.0

8.3 Propose-test-release 提议测试发布

局部敏感度的主要问题是敏感度会泄露一定的数据。如果我们尝试把局部敏感度自己变为差分隐私捏。很难，因为函数的局部敏感度的全局敏感度通常没有有限的限制。我们可以提出一个差分隐私问题然后间接获得该结果。提议的测试发布框架[9]采用了这种方法：

该框架首先要求分析人员提出一个关于所应用的函数的局部灵敏度的上界。然后，该框架运行一个差异隐私测试，以检查被查询的数据集是否“远离”一个局部灵敏度高于所提议的边界的数据集（过高的不要，已经确定上界）。如果测试通过，该框架将释放一个噪声结果，并将噪声校准到所提议的边界。

为了回答一个数据集是否“远离”一个具有高局部灵敏度的问题，我们定义了在距离𝑘处的局部灵敏度的概念。我们编写𝐴（𝑓，𝑥，𝑘）来表示𝑓通过采取远离数据集𝑥的𝑘步长而可以实现的最大局部灵敏度。从形式上讲：

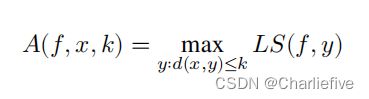
现在我们准备定义一个查询来回答这个问题：“需要多少个步骤（或者这里翻译成距离，个人认为）来实现本地敏感度大于给定上界𝑏的局部灵敏度？”

最后，我们定义了建议-测试-发布框架（见Barthe等人，图10），它满足了（𝜖，𝛿）-差异隐私：

请注意，𝐷（𝑓，𝑥，𝑏）的全局灵敏度为1：在x中添加或删除一行可能会改变与高局部敏感度（high-bound）的距离1。因此，将缩放到1/𝜖的laplace噪声相加，会产生一种差分隐私方法来测量局部灵敏度。

为什么这种方法能满足（𝜖，𝛿）的差异隐私（而不是纯粹的𝜖）的差异隐私)？这是因为他们偶然通过考试的几率为非零。在步骤2中添加的噪声可能大到足以通过测试，即使𝐷（𝑓，𝑥，𝑏）的值实际上小于满足差异隐私所需的最小距离。

这种故障模式更接近于我们从“灾难机制”中看到的灾难性故障——具有非零概率，建议-测试-发布框架允许以很小的噪声发布查询答案，以满足差异隐私。另一方面，它几乎没有灾难机制那么糟糕，因为它只要释放答案都是有噪音的。

还要注意，该框架的隐私成本是（𝜖，𝛿），即使它返回⊥（即，无论分析师是否收到答案，隐私预算都被消耗）。

让我们为我们的平均查询实现建议-测试-发布。回想一下，此查询的本地敏感度是∣𝑢/（𝑛+1）∣；增加此值的最佳方法是使𝑛更小。如果我们从数据集𝑥中采取𝑘步骤，我们就可以得到∣𝑢/（（𝑛−𝑘）+1）∣的局部灵敏度。我们可以使用下面的代码用Python来实现这个框架。

import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
import pandas as pd
import numpy as np

adult = pd.read_csv("adult_with_pii.csv")
# laplace分布
def laplace_mech(v, sensitivity, epsilon):
    return v + np.random.laplace(loc=0, scale=sensitivity / epsilon)
def pct_error(orig, priv):
    return np.abs(orig - priv)/orig * 100.0

# 局部灵敏度
def ls_at_distance(df, u, k):
    return np.abs(u / (len(df) - k + 1))
# k++ 直到到达上界b
def dist_to_high_ls(df, u, b):
    k = 0
    while ls_at_distance(df, u, k) < b:
        k += 1
    return k
# 建议-测试-发布框架 u是上界
def ptr_avg(df, u, b, epsilon, delta, logging=False):
    df_clipped = df.clip(upper=u)
    k = dist_to_high_ls(df_clipped, u, b)

    # 对k距离加噪音 使用laplace pdf中step2
    noisy_distance = laplace_mech(k, 1, epsilon)
    threshold = np.log(2/delta)/(2*epsilon)

    #代码提示
    if logging:
        print(f"Noisy distance is {noisy_distance} and threshold is {threshold}")
    if noisy_distance < threshold:
        return None
    else:
        return laplace_mech(df_clipped.mean(), b, epsilon)

#  旧方法 两步走
def gs_avg(df, u, epsilon):
    df_clipped = df.clip(upper=u)

    # noisy_sum = laplace_mech(df_clipped.sum(), u, .5*epsilon)
    # noisy_count = laplace_mech(len(df_clipped), 1, .5*epsilon)
    noisy_sum = laplace_mech(df_clipped.sum(), u, epsilon)
    noisy_count = laplace_mech(len(df_clipped), 1, epsilon)

    return noisy_sum/noisy_count

df = adult['Age']
u = 100 # 上界
epsilon = 1
delta = 1/(len(df)**2) # set delta = 1/n^2
b = 0.005  # propose a sensitivity of 0.005

result = ptr_avg(df, u, b, epsilon, delta, logging=True)
result2 = gs_avg(df, u, epsilon)
result3 = gs_avg(df, u, .5*epsilon)
print(f"方法1---{result}")
print(f"方法2---{result2}")
print(f"方法2.5---{result3}---.5*epsilon")

Noisy distance is 12561.76603061431 and threshold is 10.73744412245554
方法1---38.58363397212145
方法2---38.57408051245743
方法2.5---38.58417994405616---.5*epsilon

以上是该部分代码的复现！！！

# 就是计算实际平均值和加上全局或者局部敏感度lapalce的均值做个衡量误差
gs_results = [pct_error(np.mean(adult['Age']), gs_avg(df, u, epsilon)) for i in range(100)]
ptr_results = [pct_error(np.mean(adult['Age']), ptr_avg(df, u, b, epsilon, delta)) for i in range(100)]
_, bins, _ = plt.hist(gs_results, label='Global sensitivity')
plt.hist(ptr_results, alpha = .7, label='PTR', bins=bins)
plt.xlabel('Percent Error')
plt.ylabel('Number of Trials')
plt.legend()
plt.show()

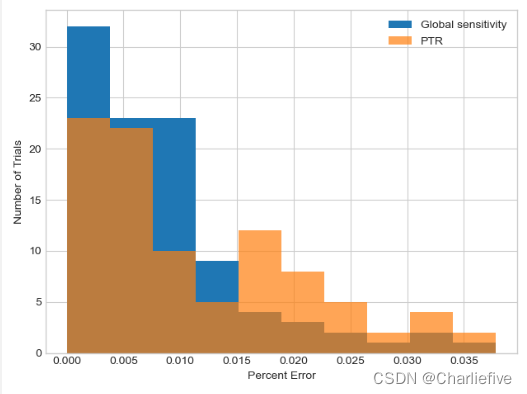
请记住，局部敏感度并不总是更好。对于平均查询，我们将查询拆分为两个单独的查询（总和和计数）的旧策略通常效果更好，这两个查询都具有有限的全局敏感性。我们可以实现具有全局敏感性的相同平均值查询：

我们可能会对提议的测试版本做得稍微好一点，但这并没有太大的区别。此外，为了使用建议测试版本，分析员必须提出一个敏感度的界限，而我们通过“魔术般地”选择一个合适的值（0.005）来欺骗。实际上，分析员需要执行几个查询来探索哪些值有效——这将消耗额外的隐私预算。

8.4Smooth Sensitivity 平滑敏感度

我们利用局部灵敏度的第二种方法称为平滑灵敏度，这是由于Nissim, Raskhodnikova, and Smith。平滑灵敏度框架，用拉普拉斯噪声实例化，提供( ϵ , δ ) -差分隐私：

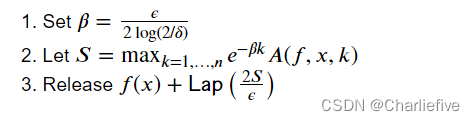
平滑灵敏度背后的思想是使用局部灵敏度的“平滑”近似值，而不是局部灵敏度本身来校准噪声。
平滑量旨在防止直接使用本地敏感度时可能发生的数据集信息意外泄漏。
上面的步骤2执行平滑：它通过与实际数据集的距离的指数函数缩放附近数据集的局部敏感性，然后取最大缩放局部敏感性。
其影响是，如果在𝑥 , 这一峰值将反映在𝑥 （因此，峰值本身是“平滑的”，并且没有显示任何关于数据集的信息）。

平滑灵敏度比提议的测试版本有一个显著的优势：它不需要分析员提议灵敏度的界限。
对于分析员来说，使用平滑灵敏度与使用全局灵敏度一样简单。然而，平滑灵敏度有两个主要缺点。

1. 首先，平滑敏感度总是大于局部敏感度（至少是2倍-见步骤3），因此可能需要比建议测试版本（甚至全局敏感度）等替代框架添加更多的噪声。
2. 第二，计算平滑敏感度需要找到所有可能值的最大平滑敏感度𝑘 , 这在计算上可能极具挑战性。

在许多情况下，可以证明考虑少量k kk的值就足够了（对于许多函数，指数衰减e^(-𝛽𝑘 ) 迅速压倒了不断增长𝐴(𝑓,𝑥,𝑘) )的值，但是对于我们想要使用的每个函数，都必须以平滑的灵敏度来证明这样的属性。

例如，让我们考虑一下我们之前定义的均值查询的平滑敏感性。

# 平滑敏感度
df = adult['Age']
epsilon = 1
delta = 1/(len(df)**2) # set delta = 1/n^2

# Step 1: set beta
beta = epsilon / (2*np.log(2/delta))
# Step 2: compute smoothed-out sensitivity for various values of k  𝐴(𝑓,𝑥,𝑘)局部敏感度
r = [np.exp(-beta * k) * ls_at_distance(df, u, k) for k in range(0, 200)]
plt.plot(r)
plt.xlabel('Value of k')
plt.ylabel('Smoothed-out Local Sensitivity')

S = np.max(r)
sensitivity = 2 * S
print(f'Final sensitivity: {sensitivity}')

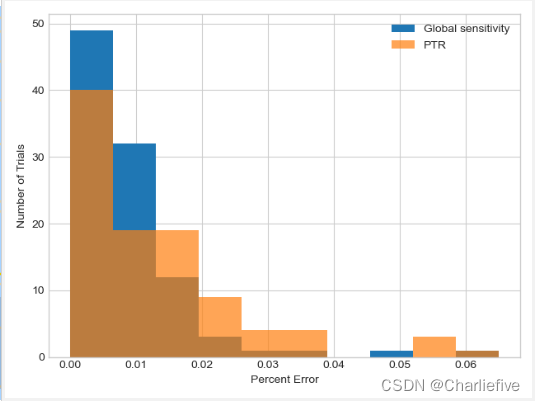
这里有两件事需要注意。首先，尽管我们只考虑𝑘 小于200，很明显，平均查询的平滑局部敏感性接近0当k接近200时。
事实上，在这种情况下，最大值出现在𝑘=0.这在许多情况下都是正确的，但如果我们想使用平滑敏感度，我们必须证明它（这里不做）。
其次，请注意，我们将用于向查询答案中添加噪音的最终敏感度高于我们之前建议的敏感度（在建议-测试-发布版本中）。这并不是一个很大的区别，但它表明，与平滑灵敏度相比，建议的测试版本有时可以实现较低的灵敏度。

8.5Sample and Aggregate样本和聚合

我们将考虑与局部灵敏度相关的最后一个框架，称为样本和聚合。对于任何函数f : D → R ，剪辑它的上下边界u和l，以下框架满足ϵ-差分隐私。

请注意，此框架满足纯𝜖 -差分隐私，它实际上不需要使用局部敏感度。事实上，我们不需要知道f（全局或局部）的敏感性。我们也不需要知道任何关于块Xi，除了他们是否相连接那一点。通常，它们是随机选择的（“好”样本往往会导致更高的准确性），但它们并不需要这样。

该框架可以通过全局敏感性和并行组合来满足差分隐私。我们将数据集拆分为𝑘 块，因此每个数据集个体都恰好出现在一个块中。我们不知道f的敏感度，但是我们对其进行了切片。由于我们去k的均值，所以全局敏感度为(u - l) / k。

请注意，我们直接声明了平均值的全局敏感性的界限，而不是将其拆分为求和和计数查询。我们无法对“常规”均值查询执行此操作，因为“常规”中值查询中的平均数取决于数据集。然而，在这种情况下，平均项目数由分析员通过选择𝑘 - 它独立于数据集。像这样的平均查询——被平均数的数量是固定的，可以公开——可以利用这个改进的全局敏感性界限。

在示例和聚合框架的这个简单实例化中，我们要求分析人员提供上限和下限𝑢 和𝑙 每个输出的𝑓(X𝑖) 。取决于𝑓 , 这可能很难做好。例如，在计数查询中，𝑓 '的输出将直接依赖于数据集。

已经提出了更高级的实例化方法（Nissim、Raskhodnikova和Smith讨论了其中的一些方法），这些方法利用了局部敏感性，以避免要求分析员𝑢 和𝑙 。
但是，对于某些函数，边界𝑓 's的输出很容易，所以这个框架就足够了。我们将考虑上面的示例-数据集中年龄的平均值-具有此属性。一个人口的平均年龄很可能在20至80岁之间，所以合理地设定𝑙=20和𝑢=80。只要我们的区块𝑥𝑖 都是人口的代表，我们不太可能在这种情况下丢失太多信息。

# Sample and Aggregate
def f(df):
    return df.mean()
def saa_avg_age(k, epsilon, logging=False):
    df = adult['Age']
    # 计算每块行数 分为k块
    chunk_size = int(np.ceil(df.shape[0] / k))
    if logging:
        print(f'Chunk size: {chunk_size}')
    # 1.分块
    xs = [df[i: i + chunk_size] for i in range(0, df.shape[0], chunk_size)]
    # 2.run f on each x_i and clip its output
    answers = [f(x_i) for x_i in xs]
    u, l = 80, 20
    clipped_answers = np.clip(answers, l, u)
    # 3.分块平均值的噪声
    noisy_mean = laplace_mech(np.mean(clipped_answers), (u-l)/k, epsilon)

    return noisy_mean

noisy_mean_result = saa_avg_age(600, 1, logging=True)
print(f"noisy_mean_result: {noisy_mean_result}")

这个框架中的关键参数是块的数量𝑘 。 像𝑘 越高，最终噪声平均值的灵敏度越低，因此块越多意味着噪声越小。
另一方面，作为𝑘 向上，每个块变小，所以每个答案𝑓(𝑥𝑖) 不太可能接近“真实”答案𝑓(𝑋) 。因为：在我们上面的例子中，我们希望每个块中的平均年龄接近整个数据集的平均年龄，如果每个块只包含少数人，这种情况就不太可能发生。
我们应该如何设置𝑘 ? 这取决于𝑓 而在数据集上，这使得它很棘手。让我们尝试各种值𝑘 来回答我们的问题