Programming Differential Privacy第九章

VARIANTS OF DIFFERENTIAL PRIVACY差分隐私的变体

学习目标:

• 定义雷尼差分隐私和零集中差分隐私
• 描述这些变体(以上两种)相对于（ε，δ）-差异隐私的优势
• 将这些变体中(以上两种)的隐私成本转换为（ε，δ）差异隐私

回想一下，我们展示的大多数隐私成本限制都是上限，但它们有时代表非常宽松
上限 - 真正的隐私成本远低于上限。
开发差分隐私的新变体的主要动机是实现更严格的隐私成本限制 - 特别是对于迭代算法 - 同时保持在实践中有用的隐私定义。

开发差分隐私的新变体的主要动机是实现更严格的隐私成本限制 - 特别是对于迭代算法 - 同时保持在实践中有用的隐私定义。比如（ε，δ）-差异隐私中的灾难性故障模式是不可取的。

我们将在本节中看到的变体可以为某些类型的查询提供更紧密的组合（降低上限），同时消除灾难性故障模式。

ε-差分隐私和顺序组合的对比

让我们快速看一下我们已经看到的工具;我们将首先看ε-差分隐私的顺序组合。事实证明，ε-差分隐私的顺序组合是紧密的。那是什么意思？这意味着有一个反例无法满足任何下限：
• 存在满足ε - 差分隐私的机制 F
• 当组合 k 次时，F 满足 kε - 差分隐私
• 但 F 不满足任何 c < k 的 cε - 差分隐私

可视化的一种巧妙方法是查看当我们“矢量化”查询时隐私成本会发生什么变化：也就是说，我们将大量查询合并到一个查询中，该查询返回单个答案的向量。
因为答案是一个向量，我们可以只使用一次向量 - 价值的拉普拉斯机制，并完全避免组合。

1. 下面，我们将绘制k个查询需要多少噪声，首先在顺序组合下，然后使用“矢量化”形式。
   在顺序组合情况下，每个查询的敏感度为 1，因此每个查询的噪声范围为 1/εi。
   如果我们想要总隐私成本为ε， 然后εi s 加起来必须是ε， 因此εi = ε/k。这就意味着每个查询得到的Laplace噪声的规模均为k/ε

2. 在向量化例子中，仅有一个查询，但是它有L1(k个)的敏感度
   因此这个例子中噪声的规模也是k/ε

import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
import pandas as pd
import numpy as np

adult = pd.read_csv("adult_with_pii.csv")
def laplace_mech(v, sensitivity, epsilon):
    return v + np.random.laplace(loc=0, scale=sensitivity / epsilon)
def pct_error(orig, priv):
    return np.abs(orig - priv)/orig * 100.0

ks = np.linspace(1, 10, 20)
epsilon = .1

# L1 sensitivity of each query: 1
# noise per query: 1/epsilon
# number of queries: k
noises_seq = [k*(1/epsilon) for k in ks]
plt.plot(ks, noises_seq, label='Sequential Composition')

# number of queries: 1
# L1 sensitivity of each query: k
# noise per query: k / epsilon
noises_11 = [1*(k/epsilon) for k in ks]
plt.plot(ks, noises_11, label='Vectorized')
plt.title('Laplace Mechanism: Vectorized vs. Composition')
plt.xlabel('Number of Queries')
plt.ylabel('Scale of Noise')
plt.legend()
plt.show()

此时两条线重合了
结论：
这两条线完全重叠。这意味着，无论我们运行多少查询，在ε - 差分隐私下，我们都无法比顺序组合做得更好。这是因为顺序组合与矢量化查询一样好，我们没有比这更好的了。

(𝜖,𝛿)-differential privacy和高级组合

那么（ε，δ）- 差分隐私呢？这就有些不同了。在顺序组合的情况下，我们可以使用高级组合定理。但是总的隐私成本正好是（ε，δ）

δ拆成两半，一半用于查询，一半用于高级组合。
通过高级组合，所有k查询的总隐私成本为（ε，δ）
根据高斯机制，噪声的尺度为：
很容易可以推出来

在“矢量化”的情况下，我们只有一个查询，L2敏感度为√𝑘
根据高斯机制，噪声的尺度是: 之前学过

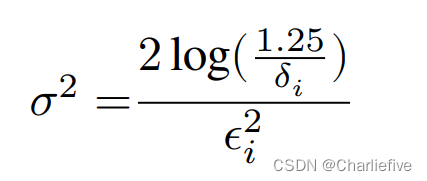
这种差异在实践中意味着什么？两者在𝑘, 但是有不同的常数，并且高级组合案例中有一个额外的对数因子𝛿. 所有这些加起来，对于高级组合来说，界限要宽松得多。让我们像以前那样把这两个图形画出来。

相比较而言"矢量化"版本增长得更慢。这是什么意思？我们应该能够在顺序组合方面做得更好！

ks = np.linspace(1, 100, 20)
epsilon = .1
delta = 1e-5

# L2 sensitivity of each query: 1
# number of queries: k
noises_seq = [16*k*np.log(1.25/delta)*np.log(1/delta)/(epsilon**2) for k in ks]
# noises_seq = [16*k*np.log(2/delta)*np.log(2.5*k/delta)/(epsilon**2) for k in ks]
plt.plot(ks, noises_seq, label='Advanced Composition')

# number of queries: 1
# L2 sensitivity of each query: sqrt(k)
noises_l1 = [2*k*np.log(1.25/delta)/(epsilon**2) for k in ks]
plt.plot(ks, noises_l1, label='Vectorized')
plt.title('Gaussian Mechanism: Vectorized vs. Composition')
plt.xlabel('Number of Queries')
plt.ylabel('Scale of Noise')
plt.legend()
plt.show()

9.1 Max Divergence and Rényi Divergence最大散度和雷尼散度

事实证明，差异隐私的定义可以直接用所谓的最大散度来表述。
在统计学中，分歧是衡量两个概率分布之间距离的一种方法，这正是我们想要为差分隐私做的。最大散度是Kullback–Leibler散度的最坏模拟，也是最常见的此类度量之一。

两个概率分布之间的最大散度𝑌 和𝑍 定义为：

这看起来很像𝜖-差异隐私！

特别是，事实证明𝐹 满足𝜖-差异隐私，如果：

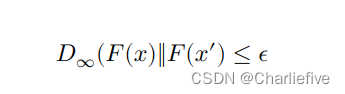
差异隐私研究的一个有趣方向是从以下方面探索其他隐私定义其他分歧。

其中，Rényi散度特别有趣，因为它（如最大分歧）也允许我们恢复不同隐私的原始定义。

Rényi散度𝛼 概率分布之间𝑃 和𝑄 定义为（其中𝑃(𝑥) 表示的概率密度𝑃 在点𝑥)：

如果我们设置𝛼 = ∞, 然后我们立即满足𝜖-差分隐私

显而易见的问题出现了：如果我们设置𝛼 去做其他事情？

可以利用Rényi散度推导出真正有趣的差分隐私松弛，它允许更好的组合定理，同时避免了可能满足(𝜖, 𝛿)-差别隐私的“灾难”的可能性。

9.2 Rényi Differential Privacy Rényi差分隐私

2017年，Ilya Mironov提出了Rényi差分隐私（RDP）。

随机机制𝐹 满足(𝛼, ̄𝜖)-RDP（如果适用于所有相邻数据集）𝑥 和𝑥′

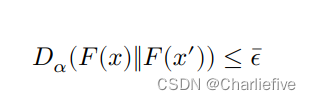
换句话说，RDP要求𝐹(𝑥) 和𝐹(𝑥′)之间的顺序𝛼的Rényi发散被 限定。注意，**我们使用 ̄𝜖来表示RDP的𝜖 参数，以便将其和纯 𝜖 - 差分隐私以及(𝜖, 𝛿)-差别隐私中的𝜖 区分出来。**

Rényi差分隐私一个关键属性是，满足RDP的机制也满足(𝜖, 𝛿)-差分隐私。具体来说，如果F满足(𝛼, ̄𝜖)-RDP，则对于𝛿 > 0，F满足(𝜖, 𝛿)-差分隐私中𝜖如下：
𝛿的值任意选择，但是应该有意义，比如（𝛿 <= 1/n^2）

实现差分隐私基本机制是高斯机制。对于L2敏感性的Δ𝑓函数𝑓 ∶ 𝒟 → ℝ𝑘，以下机制满足(𝛼, ̄𝜖)-RDP

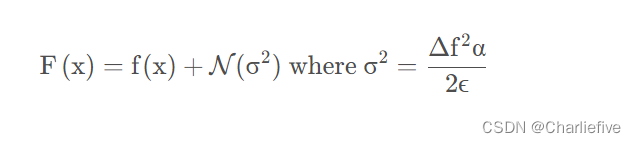
def gaussian_mech_RDP_vec(vec, sensitivity, alpha, epsilon):
    sigma = np.sqrt((sensitivity**2 * alpha) / (2*epsilon))
    return [v + np.random.normal(loc=0, scale=sigma) for v in vec]

Rényi差分隐私的主要优点是高斯机制的紧密组合，而这种组合优势不需要特殊的高级组合定理

Rényi差分隐私的顺序组成定理指出：

如果F1满足(𝛼, ̄𝜖1)-RDP
并且F2满足(𝛼, ̄𝜖2)-RDP
则他们的组合满足(𝛼, ̄𝜖1 + 𝜖2)-RDP

基于这个顺序定理，运行(𝛼, ̄𝜖)-RDP机制k此得到(𝛼, ̄𝜖k)-RDP。对于给定的噪声水平（即𝛿^2的给定值），使用RDP的顺序组合限制重复应用高斯机制的隐私成本，转化为(𝜖, 𝛿)-差分隐私(𝜖, 𝛿)-差分隐私，**通常会比直接在(𝜖, 𝛿)-差分隐私中执行合成（高级合成）中有低得多的隐私成本**。

因此，Rényi差分隐私背后的思想已被用于在最近的许多迭代算法中大大改善隐私成本会计，包括Google的Detensorflow的差异私有版本。

最后，与差分隐私的其他变体一样，RDP 提供了后处理属性。

9.3Zero-Concentrated Differential Privacy零集中差分隐私

在2016年发布的工作中，Mark Bun和Thomas Steinke提出了零集中差分隐私（zCDP）。与 RDP 一样，zCDP 是根据 Rényi 散度来定义的，但它只包含一个隐私参数 (𝜌)。随机机制F满足𝜌-zCDP，如果对于所有相邻数据集x和x` ，以及所有𝛼 ∈ (1, ∞)

这是一个比RDP更强的要求，因为它限制了许多阶数𝛼的Rényi散度。但是，随着𝛼的增长，边界会变得更加宽松。

和RDP一样，zCDP可以转化为(𝜖, 𝛿)-差分隐私：
如果F满足𝜌-zCDP，那么对于𝛿>0，F满足(𝜖, 𝛿)-差分隐私：

zCDP也与RDP相似，因为高斯机制可以用作基本机制。
具体来说，对于L2敏感性的Δ𝑓函数𝑓 ∶ 𝒟 → ℝ𝑘，以下机制满足𝜌-zCDP：

def gaussian_mech_zCDP_vec(vec, sensitivity, rho):
    sigma = np.sqrt((sensitivity**2) / (2 * rho))
    return [v + np.random.normal(loc=0, scale=sigma) for v in vec]

与RDP的另一个相似之处是，zCDP的顺序组成对于高斯机制的重复应用也是渐近紧密的。

如果F1满足𝜌1-zCDP
并且F2满足𝜌2​-zCDP
则他们的组合满足𝜌1 + 𝜌2​-zCDP

最后，zCDP 还提供了后处理属性。

9.5Composition under Variants of Differential Privacy差分隐私变体的组合情况

在以下情况下，这些变体将显著收紧隐私成本的界限：

1. 使用高斯机制（特别是在高维向量上）
2. 所讨论的算法多次应用该机制（例如数百或数千次）

为了使用 RDP 和 zCDP，我们通常会根据要使用的变体实现一个算法，然后将运行该算法的总隐私开销转换为(𝜖, 𝛿)-差分隐私，以便我们可以将其与其他算法进行比较。

为了看到这个策略的效果，让我们想象一个应用高斯机制的算法𝑘 次。我们将确定𝜎 （即在每个𝑘 迭代）和𝛿, 然后比较决赛𝜖为每个变体实现。

我们将看到，对于添加的相同数量的噪声，RDP 和 zCDP 下的合成会导致ϵ 的值变小。该算法在所有变体下都是相同的（即，它在每种情况下都会添加相同数量的噪声） - 因此这意味着RDP和zCDP为同一算法提供了更严格的隐私成本限制。

一下这段代码存在许多疑问，放在以后学完DWork的差分隐私的理论之后再来学习。

sigma = 200.0
delta = 1e-5
lap_eps = 2*sigma**2
xs = np.linspace(0, 500, 100)

gauss_eps = np.sqrt(2 * np.log(1.25/delta) / sigma**2)

ys_gauss_adv = [2 * gauss_eps * np.sqrt(2 * x * np.log(1/delta)) for x in xs]

rho = 1/(2*sigma**2)
ys_gauss_zcdp = [(x*rho) + 2*np.sqrt((x*rho) * np.log(1/delta)) for x in xs]

alpha = 60
rdp_eps = alpha / (2*sigma**2)

ys_gauss_rdp = [(x*rdp_eps) + np.log(1/delta)/(alpha-1) for x in xs]

ys_moments = [4*np.sqrt(x*np.log(1/delta))/sigma for x in xs]

plt.plot(xs, ys_gauss_adv, label="Gaussian+Adv. Comp.")
plt.plot(xs, ys_gauss_zcdp, label="Gaussian+zCDP")
plt.plot(xs, ys_gauss_rdp, label="Gaussian+RDP")
#plt.plot(xs, ys_moments, label="Moments Accountant")

plt.xlabel('Number of Iterations')
plt.ylabel('Epsilon')
plt.ylim(0, 3.0)

首先要注意的是，在 zCDP 或 RDP 下使用顺序组合比使用带有(ϵ,𝛿)-差分隐私的高级组合要好得多。使用高斯机制构建迭代算法时，应始终使用这些变体。

要注意的第二件事是zCDP（橙色）和RDP（绿色）之间的区别。

RDP的ϵ在k中线性增长，因为我们已经固定了α的值。zCDP的ϵ在k中亚线性增长，因为其有效考虑了很多α。两条线的触点为k，具体取决于RDP选择的α的值。（对于α = 20，他们大致接触k = 300）

这种差异的实际效果是，在使用RDP时必须仔细选择α，以便尽可能严格地约束隐私成本。这通常很容易做到，因为算法通常由α 参数化。结果，**我们可以简单地测试α 的多个值，看看哪一个值导致最小的相应ϵ **。

由于此测试独立于数据（它主要取决于我们选择的隐私参数以及我们要运行的迭代次数），因此我们可以根据需要测试任意数量的α值，而无需支付额外的隐私费用。我们只需要测试α 的一小部分值 （ 通常在 2 到 100 之间的范围内，即可找到最小值。这是大多数实际实现中采用的方法，包括Google的Tensorflow隐私保护版本。