基于MATLAB的列车防护曲线组合步长算法分析与仿真验证

rgb2gray

已于 2024-01-27 15:48:36 修改

阅读量4.5k

点赞数 2

分类专栏：列车运行控制文章标签： ATP曲线 MATLAB 列车运行控制列车防护曲线

于 2021-06-16 00:22:23 首次发布

本文链接：https://blog.csdn.net/weixin_44026026/article/details/117935749

版权

列车运行控制专栏收录该内容

6 篇文章

订阅专栏

本文探讨了基于MATLAB的列车防护曲线算法，重点研究了速度步长、时间步长和距离步长对ATP超速防护精度的影响。通过仿真验证，发现时间步长与距离步长方法的精度优于速度步长，并提出了组合步长方法以提高精度。在精度分析中，利用梯度函数评估了曲线精度，并给出了组合步长模型的实施细节和仿真结果。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

基于MATLAB的列车防护曲线组合步长算法分析与仿真验证

说明：本文即本人城市轨道交通控制课程的课程设计，参考了一些论文，并提出了一些创新（算法精度的比较部分），附有个人编写的MATLAB代码，可能会有一些小错误，欢迎大家交流！

列控系统中，只要与列车运行安全有关的问题，ATP都要进行防护。然而，运行安全的主要问题是列车运行速度的防护，故而经常将ATP子系统也称为“速度防护”或“超速防护”系统。所以，对车载ATP系统模型进行研究，重点在于研究ATP超速防护曲线算法。列车超速防护曲线主要是按照取步长的方式通过牵引计算得到的。经过前人多年的研究，普通铁路线路上的牵引计算已经比较成熟了。然而，随着高速铁路的发展，其准确性和精细化设计要求更高，特别是CTCS3级列控系统中，动车的高速度及高密度运行对列车制动精度提出了更高的要求。在CTCS3级列控系统中，车载ATP采用基于准移动闭塞的速度-目标距离曲线模式，因此，本论文主要针对速度-目标距离模式下ATP防护曲线中步长的选取进行研究。

1.1速度步长

取速度为步长的方法就是把整个制动过程分成若干个速度间隔，假设列车在每个速度间隔内制动合力不随速度变化而变化。则根据前面讨论的列车运行动力学公式和列车制动距离计算方法，可得列车的时间增量和距离增量为：
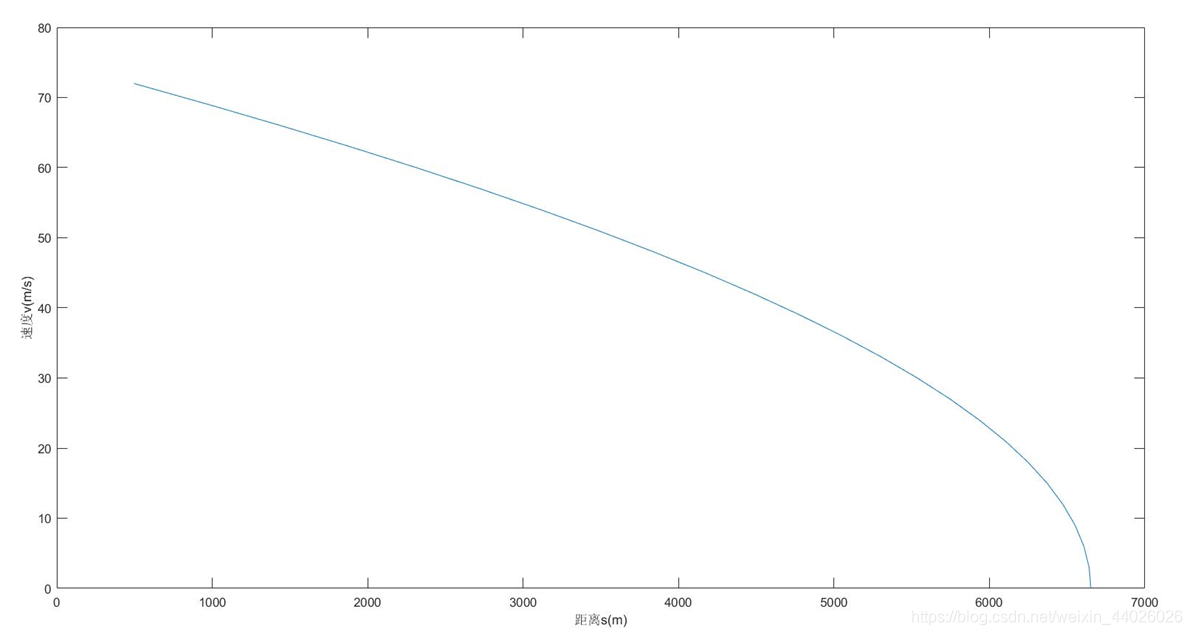
在这里插入图片描述

1.2时间步长

取时间为步长的方法就是把整个制动过程细分为若干个时间段，在时间内，列车加速度恒定，列车的制动合力是一个常数。则根据前面讨论的列车运行动力学公式和列车制动距离计算方法，可得列车的速度增量和距离增量为：
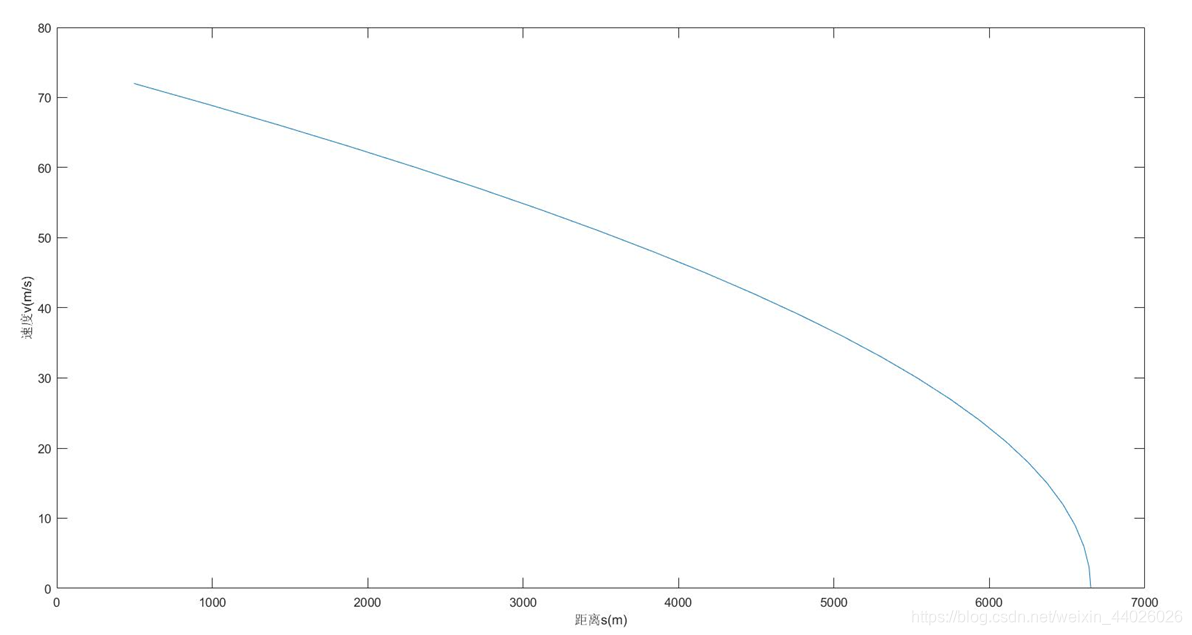
在这里插入图片描述

1.3距离步长

取距离为步长的方法就是把整个制动过程分成n个长度为的小区段，列车在每个距离区段内制动合力不随位移的变化而变化。则根据前面讨论的列车运行动力学公式和列车制动距离计算方法，可得列车的速度增量和时间增量为：
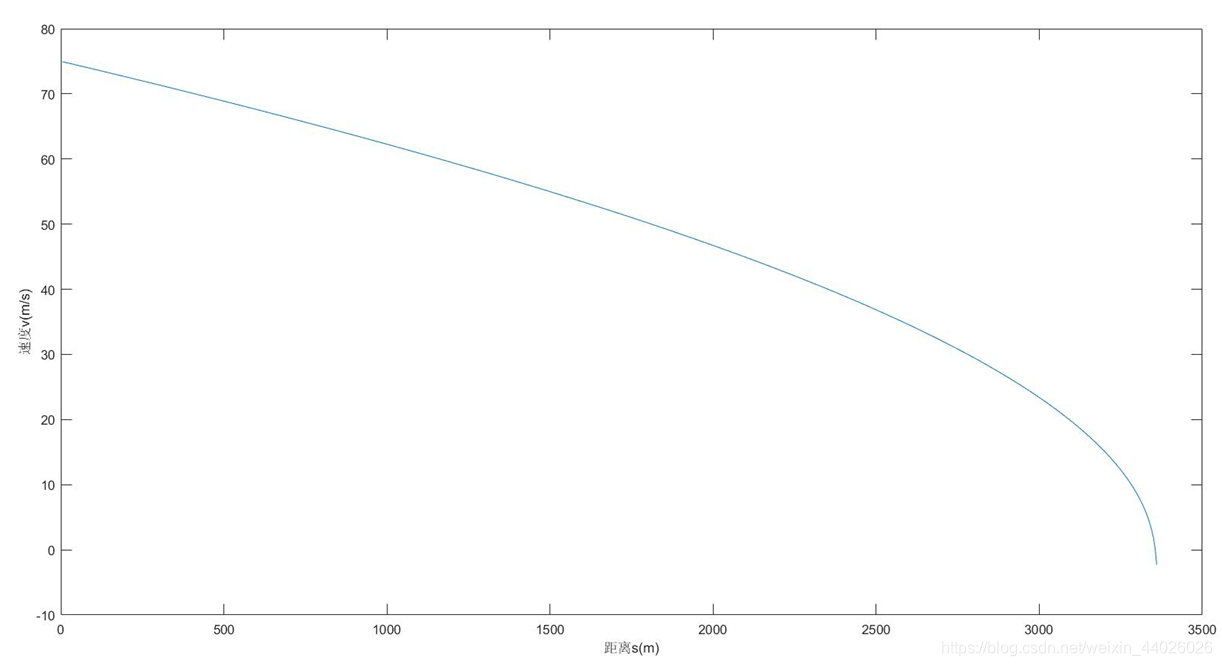
在这里插入图片描述

2.ATP防护曲线的仿真

在研究了车载ATP防护曲线算法的基础上，本章主要完成车载ATP防护曲线的仿真实现，以及对车载ATP防护曲线算法进行验证分析。在仿真实现之前，首先要从车载设备存储的固定信息里，提取出线路数据，结合存储在车载设备上的列车自身的性能参数：列车阻力、制动率、旋转质量系数、空走时间等，实现列车的牵引计算，计算出列车当前位置到目标点的速度-目标距离防护曲线。算法的实现过程中，要考虑到线路坡道、隧道、弯道和线路限速等线路条件对制动曲线的影响。ATP防护曲线的仿真系统流程图如图5-1所示。
车载ATP接收到的移动授权包括了目标点的位置和速度，然后利用第4章讨论的方法，将目标距离分成N个小区段，从已知目标点的目标速度向较高速度方向进行反向计算。在计算每个小区段的初速度和位置时，要先获得当前位置的最具限速度，比较当前速度与最具限速度的大小，若当前速度小于最具限速度，然后计算当前位置的加速度，根据图速度控制曲线仿真算法流程图计算区段初速度，同时计算区段初位置。如当前速度大于最具限速度，则区段初速度等于最具限速度。如此循环，直到计算到列车所在位置。

2.1基于组合步长的ATP防护曲线的仿真验证

根据上一章的内容可知，通过列车制动距离计算模型的分析，在列车制动过程中，速度在连续变化，列车制动合力也不断变化，即列车加速度也是连续变化的，因此采用取步长的方法进行计算。取步长的方法可分为时间步长，距离步长，速度步长。在计算过程中，选择不同参数的步长或者步长的长短取得不同，计算结果的精确度、函数的收敛速度以及数据的时效性都会是不同的。
首先画出速度步长，时间步长与距离步长的散点图，可大致得知模拟的精确度，如图5-1，5-2，5-3所示。
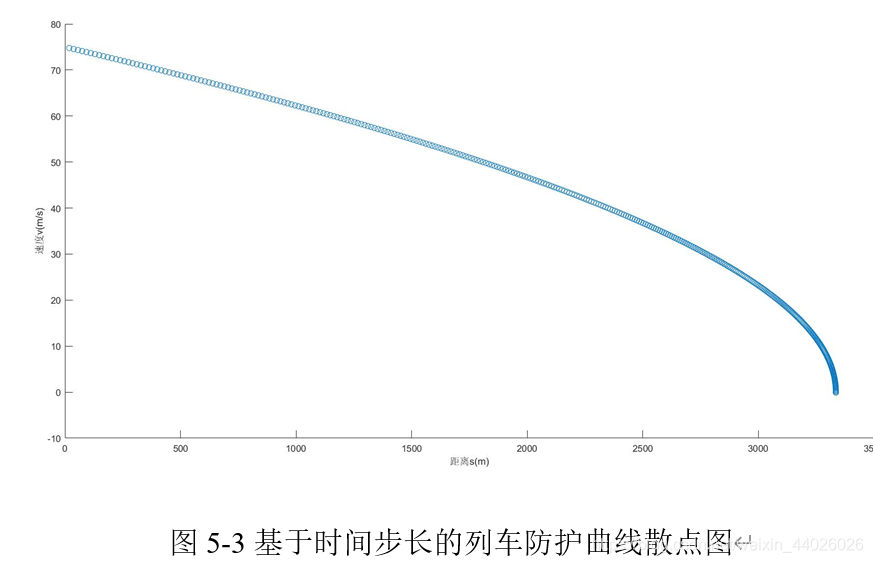
在这里插入图片描述

由图5-1，图5-2与图5-3对比可以得出，时间步长与距离步长方法的精度远远高于速度步长方法，所以摒弃速度步长方法。观察到时间步长方法与距离步长方法在精度上仍有差距，所以本文提出组合步长的方法，即结合时间步长与距离步长，提升ATP曲线精度。
对于ATP曲线图像，横坐标为距离s（m），纵坐标为速度v（km/h），根据第4章得到的ATP制动模型所得到的数据点是离散的，对于绘制出的ATP曲线的精度可以用两个数据点间横坐标的差来描述，两点之间横坐标的差越大就意味着两点之间的间距越大，对应的散点图数据的分布就越稀疏，精度就越差。
若将数据点横坐标的集合看作一维向量，点之间的间距假定为 1。使用MATLAB中的gradient函数即可求出向量的一维数值梯度，输出 FX 对应于，即 x（水平）方向上的差分，可以用x方向上的差分来表示ATP曲线的精度，如图5-5，图5-6所示。
在这里插入图片描述

由图5-5，图5-6可以看出，时间步长法x方向差分的值是单调下降的，即绘制出的该ATP曲线精度是单调下降的，而距离步长法x方向差分的值维持在5左右。所以对于该ATP曲线，在x方向差分等于5之前选取时间步长法模型来绘制ATP曲线，而在x方向差分等于5之后选取距离步长法模型来绘制ATP曲线，这样精度较高。
最后，采用组合步长模型绘制出的列车防护曲线散点图如图5-7所示，ATP制动曲线如图5-8所示。
在这里插入图片描述

3.参考文献

[1]窦蓉. 车载ATP制动曲线仿真研究[J]. 信息化研究, 2012, 038(005):42-44.
[2]赵泽良. 基于CBTC列车的ATP安全制动曲线计算模型研究[J]. 城市建设理论研究:电子版, 2012(16).
[3]胡晓娟, 陈铁, 邸建红. CTCS-3级列控系统ATP超速防护曲线的仿真[J]. 科技通报, 2018, v.34;No.237(05):147-150.

部分MATLAB代码：

%-----------------------------------------------------------
%2021.05.02
%by YYC
%组合步长的ATP曲线
%-----------------------------------------------------------

clear all;clc;
i=2.1;  %坡度
r=400;  %曲率半径
ls=4000;  %隧道长度
wi=i;   %列车坡道附加阻力
wr=600/r;  %列车弯道附加阻力
ws=0.00013*ls; %列车隧道附加阻力
dt=0.25;
v_0=270/3.6;
y=0.06; %回转质量系数
b=81.04; %列车单位制动力
g=9.8;

%速度步长
v1=v_0;
s1=0;
i=1;
dv_0=3;
while(v1>0)
    w0=0.79+0.0064*v1*3.6+0.000115*v1*v1*3.6*3.6;  %列车单位基本阻力
    v1=v1-dv_0;
    ds=1000*(1+y)*((v1+3)*(v1+3)-v1*v1)/(g*(b+w0+wi+wr+ws));
    s1=s1+ds;
    vv0(i)=v1;
    ss0(i)=s1;
    i=i+1;
end


%%
%时间步长
v1=v_0;
s1=0;
i=1;
while(v1>0)
    w0=0.79+0.0064*v1*3.6+0.000115*v1*v1*3.6*3.6;  %列车单位基本阻力
    dv=g*(b+w0+wi+wr+ws)*dt/(1000*(1+y));
    v1=v1-dv;
    ds=v1*dt+g*(b+w0+wi+wr+ws)*dt*dt/(2000*(1+y));
    s1=s1+ds;
    vv1(i)=v1;
    ss1(i)=s1;
    i=i+1;
end



%%
%距离步长
i=1;
v2=v_0;
dx=5;
dv=0;
s2=0;
while(v2>0)
    w0=0.79+0.0064*v2*3.6+0.000115*v2*v2*3.6*3.6;  %列车单位基本阻力
    dv=sqrt(v2*v2+(2*g*(b+w0+wi+wr+ws)*dx)/(1000*(1+y)))-v2;
    v2=v2-dv;
    vv2(i)=v2;
    s2=s2+dx;
    ss2(i)=s2;
    i=i+1;
end



gra1=gradient(ss1);
gra2=gradient(ss2);