交互式多模型-无迹卡尔曼滤波IMM-UKF——CV/CT/CA模型交互机动目标跟踪（模型维数不同IMM算法设计）

交互式多模型-无迹卡尔曼滤波IMM-UKF——CV/CT/CA模型交互机动目标跟踪（模型维数不同IMM算法设计）

原创不易，路过的各位大佬请点个赞

针对机动目标跟踪的探讨、技术支持欢迎联系，也可以站内私信
WX: ZB823618313

基于IMM机动目标跟踪算法设计最重要的核心部分主要包括：

1. IMM框架
2. 滤波器选择：(这里基于UKF)
3. 目标运动模型：（这里基于CV CT）

1. 难点分析

针对机动目标跟踪问题，如果交互式多模型IMM框架、如模型转移概率、模型集合以及模型概率初始等确定时，IMM算法的实现（设计）主要存在两大难点：

1- 非线性滤波器的选择和集成

2- 模型集合多样、不统一
在IMM算法设计中，模型多样最直接的一个问题就是戈尔戈模型的状态维数不同，而IMM 的总体（混合）估计却只存在一个统一的状态维数，因此这就导致了很多模型组合不能直接适用于IMM 算法中。

以二维目标为例，CV模型的状态维数4，而CA模型的状态维数6，CT模型的状态维数存在两种情形4和5，singer模型状态维数为6，Jerk模型的状态维数为8，等等。这直接导致IMM滤波器状态失配。

2. 设计思路/解决方案

以典型组合
模型1：匀速运动CV（4维）
模型2：匀速转弯运动CT(4维)
模型3：匀加速运动CA（6维）
为例，进行分析。

其它不同维数的模型组合可以基于该思想，很容易的推广。哈哈哈哈哈哈啊哈哈哈，一学就会，…

2.1 CV模型： $X=[x,y,\dot{x},\dot{y}{]}^T$

$$X_{k+1}=\left[\begin{array}{cccc}1& 0& T& 0\\ 0& 1& 0& T\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]X_k+W_k$$
其中$W_k$为零均值白噪声，其方差为：
$$Q_k=q_k^2\left[\begin{array}{cccc}{T}^3/3& T^2/2& 0& 0\\ T^2/2& T& 0& 0\\ 0& 0& T^3/3& T^2/2\\ 0& 0& T^2/2& T\end{array}\right]$$
定义矩阵
$F{k}_1=\left[\begin{array}{cccc}1& 0& T& 0\\ 0& 1& 0& T\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$, $F{k}_{cv}=\left[\begin{array}{cc}F{k}_1& \\ & 0_2\end{array}\right]$

2.2 CT模型： $X=[x,y,\dot{x},\dot{y}{]}^T$

$$X_{k+1}=\left[\begin{array}{cccc}1& \frac{\sin (\omega T)}{\omega }& 0& -\frac{1-\cos (\omega T)}{\omega }\\ 0& \cos (\omega T)& 0& -\sin (\omega T)\\ 0& \frac{1-\cos (\omega T)}{\omega }& 1& \frac{\sin (\omega T)}{\omega }\\ 0& \sin (\omega T)& 0& \cos (\omega T)\end{array}\right]X_k+W_k$$
其中$W_k$为零均值白噪声，其方差为：
$$Q_k=q_k^2\left[\begin{array}{cccc}{T}^3/3& T^2/2& 0& 0\\ T^2/2& T& 0& 0\\ 0& 0& T^3/3& T^2/2\\ 0& 0& T^2/2& T\end{array}\right]$$
或者为(两种形式都可以用，下面一代码形式给出)

Qk= q2*[2*(w1*T-sin(w1*T))/w1^3     0        (1-cos(w1*T))/w1^2                 (w1*T-sin(w1*T))/w1^2     ;
         0        2*(w1*T-sin(w1*T))/w1^3         -(w1*T-sin(w1*T))/w1^2                 (1-cos(w1*T))/w1^2  ;
         (1-cos(w1*T))/w1^2              -(w1*T-sin(w1*T))/w1^2   T                   0        ;
         (w1*T-sin(w1*T))/w1^2           (1-cos(w1*T))/w1^2     0                T;];

定义矩阵

$F{k}_2=\left[\begin{array}{cccc}1& \frac{\sin (\omega T)}{\omega }& 0& -\frac{1-\cos (\omega T)}{\omega }\\ 0& \cos (\omega T)& 0& -\sin (\omega T)\\ 0& \frac{1-\cos (\omega T)}{\omega }& 1& \frac{\sin (\omega T)}{\omega }\\ 0& \sin (\omega T)& 0& \cos (\omega T)\end{array}\right]$, $F{k}_{ct}=\left[\begin{array}{cc}F{k}_2& \\ & 0_2\end{array}\right]$

2.3 CA模型 ：$X=[x,x,\dot{x},\dot{y},\ddot{x},\ddot{y}{]}^T$

$$X_{k+1}=\left[\begin{array}{cccccc}1& 0& T& 0& T^2/2& 0\\ 0& 1& 0& T& 0& T^2/2\\ 0& 0& 1& 0& T& 0\\ 0& 0& 0& 1& 0& T\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right]X_k+W_k$$
其中$W_k$为零均值白噪声，其方差为：

Qk3=q3^2*[T^5/20   0      T^4/8  0       T^3/6   0;
          0       T^5/20  0      T^4/8   0       T^3/6;
          T^4/8   0       T^3/3  0       T^2/2   0;
          0       T^4/8   0      T^3/3   0       T^2/2;
          T^3/6   0       T^2/2  0       T       0
          0       T^3/6   0      T^2/2   0       T];

定义矩阵
$F{k}_3=\left[\begin{array}{cccccc}1& 0& T& 0& T^2/2& 0\\ 0& 1& 0& T& 0& T^2/2\\ 0& 0& 1& 0& T& 0\\ 0& 0& 0& 1& 0& T\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right]$, $F{k}_{ca}=F{k}_3$

2.4 IMM滤波器状态维数设计

滤波状态设计为：
$$X=[x,x,\dot{x},\dot{y},\ddot{x},\ddot{y}{]}^T$$

目标真实航迹生成方程：
第一阶段：
$$X_{k+1}=F{k}_{cv}{X}_k+W_k$$
第二阶段：
$$X_{k+1}=F{k}_{ct}{X}_k+W_k$$
第三阶段：
$$X_{k+1}=F{k}_{ca}{X}_k+W_k$$
代码：

%% 产生真实轨迹
    for k=1:t1
        X=Fk_cv*X+Gk_cv*sqrtm(Qk1)*randn(4,1);     %产生真实轨迹
        X_true(:,k,index)=X;
    end
    for k=t1+1:t2
        X=Fk_ct*X+Gk_ct*sqrtm(Qk2)*randn(4,1);
        X_true(:,k,index)=X;
    end
    for  k=t2+1:steps
        X=Fk3*X+Gk_ca*sqrtm(Qk3)*randn(6,1);
        X_true(:,k,index)=X;
    end

这样目标状态统一为$X=[x,x,\dot{x},\dot{y},\ddot{x},\ddot{y}{]}^T$ 6维，实际上在CV和CT运动模型中，$F{k}_{ct}$和$F{k}_{cv}$最后两行均为0，因此CVCT模型对加速并没有产生任何作用，加速度的引入只是为了满足状态维数。

同样，$G{k}_{ct}$和$G{k}_{cv}$最后两行均为0，为6x4的矩阵，为了让CVCT的4路噪声满足6维状态。

存在的问题：这样用0对齐维数，直接导致CV和CT的过程噪声方差奇异、进而导致滤波估计协方差奇异，使得矩阵分解失败、没办法产生采样点。（目标大多数非线性滤波器都是基于矩近似的采样滤波，e.g.,UKF,CKF,DDF,QKF…）

2.5 IMM各模型滤波器设计

思路：采用变维思想。针对不同模型的局部滤波器，只对该模型真实包含的状态进行滤波更新，其余状态保持不变。

CV模型局部滤波：${\hat{x}}_{k|k}^{cv}=[{\hat{x}}_{k|k}(1),{\hat{x}}_{k|k}(2),{\hat{x}}_{k|k}(3),{\hat{x}}_{k|k}(4){]}^T$
$$\begin{array}{rl}{\hat{x}}_{k|k}^{cv}& ={\hat{x}}_{k|k-1}^{cv}+K_z\left(z_k-{\hat{z}}_{k|k-1}\right)\\ P_{k\mid k}^{cv}& =P_{k\mid k-1}-K_k{S}_k{K}_k^{\prime }\end{array}\text{\hspace{1em}(5)}$$
注意：滤波中采用的参数矩阵为$Fk1\in {\mathbb{R}}^4$，$Qk1\in {\mathbb{R}}^4$，上面右定义并给出。

CT模型局部滤波：${\hat{x}}_{k|k}^{ct}=[{\hat{x}}_{k|k}(1),{\hat{x}}_{k|k}(2),{\hat{x}}_{k|k}(3),{\hat{x}}_{k|k}(4){]}^T$
$$\begin{array}{rl}{\hat{x}}_{k|k}^{ct}& ={\hat{x}}_{k|k-1}^{ct}+K_z\left(z_k-{\hat{z}}_{k|k-1}\right)\\ P_{k\mid k}^{ct}& =P_{k\mid k-1}-K_k{S}_k{K}_k^{\prime }\end{array}\text{\hspace{1em}(5)}$$
注意：滤波中采用的参数矩阵为$Fk2\in {\mathbb{R}}^4$，$Qk2\in {\mathbb{R}}^4$，上面右定义并给出。

CA模型局部滤波：${\hat{x}}_{k|k}^{ca}={\hat{x}}_{k|k}$
$$\begin{array}{rl}{\hat{x}}_{k|k}^{ca}& ={\hat{x}}_{k|k-1}^{ca}+K_z\left(z_k-{\hat{z}}_{k|k-1}\right)\\ P_{k\mid k}^{ca}& =P_{k\mid k-1}-K_k{S}_k{K}_k^{\prime }\end{array}\text{\hspace{1em}(5)}$$
注意：滤波中采用的参数矩阵为$Fk3\in {\mathbb{R}}^4$，$Qk3\in {\mathbb{R}}^4$，上面右定义并给出。

代码实现：

%filer1
[xk_UKF1,Pk_UKF1,A_UKF1] = fun_2UKF_cvct(X_update_hat1,P_update_hat1,Fk1,Gk1,Z_true(:,k,index),Qk1,sigma_r,sigma_b,xp(:,1));


%filer2
[xk_UKF2,Pk_UKF2,A_UKF2] = fun_2UKF_cvct(X_update_hat2,P_update_hat2,Fk2,Gk2,Z_true(:,k,index),Qk2,sigma_r,sigma_b,xp(:,1));


%filer3
[xk_UKF3,Pk_UKF3,A_UKF3] = fun_2UKF(X_update_hat3,P_update_hat3,Fk3,Gk3,Z_true(:,k,index),Qk3,sigma_r,sigma_b,xp(:,1));

        

3. IMM-UKF仿真实现

3.1. 仿真参数

一、目标模型：CV CT CA
第一阶段：1:39s，匀速运动CV
第二阶段：40:91s，匀速圆周运动CT，角速度：$5\ast \pi /180;$
第三阶段：92:150s，匀加速运动CA

t1=39; t2=91; t3=steps;
    %% 产生真实轨迹
    for k=1:t1
        X=Fk_cv*X+Gk_cv*sqrtm(Qk1)*randn(4,1);     %产生真实轨迹
        X_true(:,k,index)=X;
    end
    for k=t1+1:t2
        X=Fk_ct*X+Gk_ct*sqrtm(Qk2)*randn(4,1);
        X_true(:,k,index)=X;
    end
    for  k=t2+1:steps
        X=Fk3*X+Gk_ca*sqrtm(Qk3)*randn(6,1);
        X_true(:,k,index)=X;
    end

二、测量模型：2D主动雷达
在二维情况下，雷达量测为距离和角度
$$\begin{gathered} r_k^m=r_k+{\tilde{r}}_k \\ {b}_k^m=b_k+{\tilde{b}}_k \end{gathered}$$
其中
$$\begin{gathered} r_k=\sqrt{(x_k-x_0{)}^{+}(y_k-y_0{)}^2)} \\ {b}_k={\tan }^{-1}\frac{y_k-y_0}{x_k-x_0} \end{gathered}$$
$[x_0,y_0]$为雷达坐标，一般情况为0。雷达量测为$z_k=[r_k,b_k{]}^{\prime }$。雷达量测方差为
$$R_k=\text{cov}(v_k)=\left[\begin{array}{cc}{\sigma }_r^2& 0\\ 0& {\sigma }_b^2\end{array}\right]$$且${\sigma }_r=70m$， ${\sigma }_b=0.3^o$。

三、性能评估
RMSE(Root mean-squared error):蒙塔卡罗次数$M=500$，${\hat{x}}_{k|k}^i$为第$i$次仿真得到的估计。
$$\text{RMSE}(\hat{x})=\sqrt{\frac{1}{M}\sum _{i=1}^M({\mathbf{x}}_k-{\hat{\mathbf{x}}}_{k|k}^i)({\mathbf{x}}_k-{\hat{\mathbf{x}}}_{k|k}^i{)}^{\prime }}$$
$$\text{Position RMSE}(\hat{x})=\sqrt{\frac{1}{M}\sum _{i=1}^M(x_k-{\hat{x}}_{k|k}^i{)}^2+(y_k-{\hat{y}}_{k|k}^i{)}^2}$$
$$\text{Velocity RMSE}(\hat{x})=\sqrt{\frac{1}{M}\sum _{i=1}^M({\dot{x}}_k-{\hat{\dot{x}}}_{k|k}^i{)}^2+({\dot{y}}_k-{\hat{\dot{y}}}_{k|k}^i{)}^2}$$
ANEES（average normalized estimation error square）,$n$ 为状态维数，${\mathbf{P}}_{k|k}^i$为第$i$次仿真滤波器输出的估计协方差

3.2. 跟踪轨迹

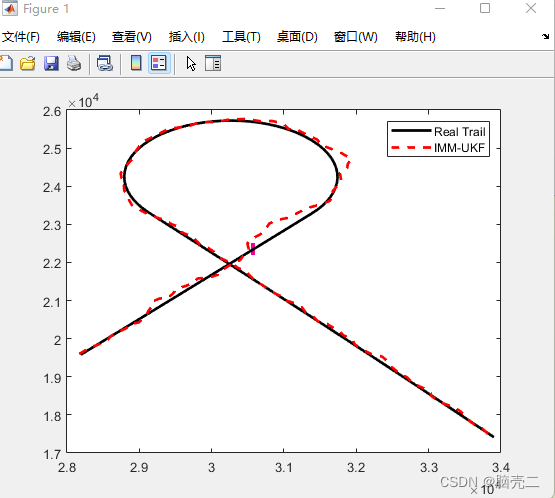
3.3. 位置/速度RMSE

4.4. 模型概率

4.5. 部分代码

%模型概率初始化
m=[0.8;0.1;0.1];
%模型转移概率
Pa=[0.8 0.1 0.1;
    0.1 0.8 0.1;
    0.1 0.1 0.8;];
Pa=[0.9 0.05 0.05;
    0.05 0.9 0.05;
    0.05 0.05 0.9;];

%误差存储
X_true=zeros(4,steps,runs);
Z_true=zeros(2,steps,runs);
X_err_IMM=zeros(4,steps,runs);
X_IMM=zeros(4,steps,runs);
PI=zeros(3,steps,runs);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%


randn('state',sum(100*clock));  %每次给不同的状态重置随机数产生器（因为clock每次都不同）

%%

for index=1:runs %蒙特卡洛次数
    index         %显示运行次数
    
    %滤波初始化
    X=X_aver_zero+sqrtm(P_zero)*randn(4,1);%产生真实X0
 %三个滤波器的初始化   
    xk_UKF1=X_aver_zero;             %X(0|0)= X_aver_zero
    Pk_UKF1=P_zero;                  %P(0|0)= P_zero
    xk_UKF2=X_aver_zero;
    Pk_UKF2=P_zero;
    xk_UKF3=X_aver_zero;
    Pk_UKF3=P_zero;
    
    t1=39; t2=91; t3=99;t4=131;t5=steps;
    %% 产生真实轨迹
    for k=1:t1
        X=Fk1*X+Gk*sqrtm(Qk1)*randn(4,1);     %产生真实轨迹
        X_true(:,k,index)=X;
    end
    for k=t1+1:t2
        X=Fk2*X+Gk*sqrtm(Qk2)*randn(4,1);
        X_true(:,k,index)=X;
    end
    for  k=t2+1:steps
        X=Fk1*X+Gk*sqrtm(Qk1)*randn(4,1);
        X_true(:,k,index)=X;
    end
% %     for  k=t3+1:t4
% %         X=Fk3*X+Gk*sqrtm(Qk3)*randn(4,1);
% %         X_true(:,k,index)=X;
% %     end
% %     for  k=t4+1:t5
% %         X=Fk1*X+Gk*sqrtm(Qk1)*randn(4,1);
% %         X_true(:,k,index)=X;
% %     end
    
    %% 状态递归实现
    for k=1:steps
        
        v=normrnd(v_mu,[sigma_r; sigma_b]);%雷达噪声
        % 雷达测量
        [r,b] = measurements2(X_true(:,k,index),xp(:,1)); %rm=距离，bm=角度 dm=多普勒速度
        rm=r+v(1);
        bm=b+v(2);
        Z_true(:,k,index)=[rm,bm]';

原创不易，路过的各位大佬请点个赞