Andrew Ng带我漫步机器学习 - 第八周 非监督学习K-means算法与PCA

集群（clustering）

---

非监督学习与监督学习的区别可以从以下几个考虑

• 原始数据没有标签
• 原始数据集没有明确关系或明显的分类特征
• 原始数据集没有y
  面对非监督学习问题，集群是常用的方法集

K-means算法

---

集群种类为K，训练样本为$x^{(i)}...i=(1,m)$，陪伴我们这么久的$x_0=1$到这里就要离开了

1. 在样本坐标系中随机初始化K个坐标点
2. 集群分配（簇分配，cluster assignment）
   对所有点，计算它们到K个点的距离，将其与距离最近的点归为义类，生成K个集群
3. 移动中心点（move centroid）
   分别计算K类中所有点各特征坐标的平均值，平均值组成的坐标为新的K点

重复以上两步，直到新的两点不再变化，视为分类完成，生成K个集群

连续集群

呈连续性的离散分布样本呢也可以使用集群，如T-shirt大小问题：

• 使用k-means进行分类
• 人为地对每一集群分类贴标签，如：大，中，小

优化目标

了解优化目标有以下几个优势：

• 帮助我们调试程序
• 帮助我们找到更好的代价函数值，避免局部最小值

参数分析

• k： 集群中心点序号
• K：集群中心点总数
• $c^{(i)}$：样本$x^{(i)}$分配到的中心点的序号
• ${\mu }_k$： 集群中心点k
• ${\mu }_{c^{(i)}}$: 样本$x^{(i)}$分配到的集群的中心点

e.g.
$x^{(i)}$ --> 5，则$c^{(i)}$=5，${\mu }_{c^{(i)}}$=${\mu }_5$

优化项（代价方程）

寻求下式全局最小值
$$J_{min}(c^{(1)},...,c^{(m)},{\mu }_1,...,{\mu }_K)=\frac{1}{m}\sum _{i=1}^m||x^{(i)}-{\mu }_{c^{(i)}}|{|}^2$$

分步优化

1. 随机初始化K
2. 在集群分配时，保持$\mu$各项不变，计算代价函数，优化$c$
3. 在移动中心点时，保持c各项不变，计算代价函数，优化$\mu$
   可见k-mean算法在优化代价函数时最大的特点就是分步计算代价函数从而获得更好的参数$c$及$\mu$

随机初始化

这是一位隐藏的大佬

初始化常规步骤

1. K < m (m为样本数量）
2. 随机选取个训练样本
3. 设置${\mu }_1,...{\mu }_k$等价于K个选取的训练样本
   

观察上图，明显不同的中心点的初始化会影响分类结果吗？答案是会的

局部优化

一定条件下，初始化K会使分类处于局部优化的情况下。此时中心点无法更好地进行全局分类，而是在一个不理想地区域“卡住”

重复法 — K-means方法使用总结

为了避免由不理想的随机初始化造成的局部优化情况，采用重复原则，筛查局部优化情形

没错，就像图里这样简单粗暴，怕出错就多试几（百）次

• 重复次数选择在50-1000之间为宜
• 选择所有得出的代价函数值中最小的哪一项

如此就是运行K-means方法的完整步骤了

选择K

问题来了，数据没有标签，到底怎么样确定K呢？

法一 — 找肘子

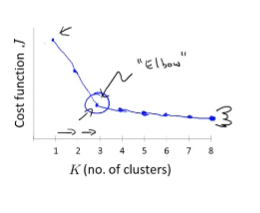
看到肘子没有，没错，就选三

法二 — 问自己

不可能所有函数分布都像肘子一样，这个时候，你就只能根据问题需求来自己提供答案

如图，你想要将衬衫分为K种就自己选K

数据降维

---

数据压缩不是要你减少数据，也不是数据的byte减少了，更不是压缩。机器学习中的数据压缩主要就是降低数据维度

2D --> 1D

线性回归模型中，可以将坐标点垂直映射到近似回归曲线

• 映射后的数据是近似的，不是完全等价的
• 降低维度显著降低了计算量

对于非线性模型，我们应该怎么办呢？仍然选择一条直线进行映射，但是近似度降低，模型也就不那么准确了

3D --> 2D

1. 旋转3维平面，寻找数据呈现最像一条直线的视角
2. 在该视角平面上选择向量$z_1,z_2$，两向量垂直，且数据都分布在第一象限间
3. 映射坐标，去除垂直于所选坐标的维度

综上，你需要一款能够把数据转来转去的软件

数据可视化

数据可视化本身不能降低维度，要先根据问题需求减少特征量，然后再进行数据可视化

数据在每个维度都有大量的特征，而我们的目标是分析每个国家GDP和人均GDP的情况

降低维度，使用$z_1,z_2$直观地表达GDP和人均GDP

根据$z_1.z_2$两个维度画出二维图，标点分类

PCA

---

Principal Component Analysis，主成分分析

前面我们提到数据降维时采取的映射是近似的，那就代表存在误差，而PCA正是为了最小化映射误差

误差计算：投影点至投影目标的垂直距离之和

PCA投影

• PCA是垂直投影，误差计算也为计算垂直距离
• PCA与线性回归完全不同（其它回归也一样）
  
  由图，线性回归计算的是y方向的距离，而PCA计算的是垂直方向
• 对于三维模型，PCA要找到两个使垂直距离最小的矢量，且这连个矢量垂直且共点，能够组成平面
  

数据处理

对输入集运行规模缩放或均值均一化

1. 计算均值${\mu }_i=\frac{1}{m}{\sum }_{i=1}^m{x}_j^{(i)}$
2. 用$x_j-{\mu }_j$替换$x_j^{(i)}$项
3. 如果特征项规模不同，缩放特征量使特征量在合理范围内，$x_j^{(i)}\leftarrow \frac{x_j^{(i)}-{\mu }_j}{s_j}$
   

算法实现

从底层实现PCA算法几乎是不现实的，我们仍然使用现存的函数库进行处理

以下部分为将n维矩阵降低至k维矩阵的PCA算法

1. 计算协方差矩阵 Sigma
   $$\Sigma =\frac{1}{m}\sum _{i=1}^m(x^{(i)})(x^{(i)}{)}^T$$
2. 计算特征向量，使用svd方程
   得到三个矩阵（见上图），其中有用的矩阵是U
3. 提取U矩阵，进行计算，获得z矢量
   
   提取U矩阵的前K项矢量，转置后与样本相乘，得到目标矢量$z^{(i)}$，代表着样本点i降维后在新坐标系的坐标

PCA应用指南

---

投影坐标回建

由已知投影坐标z回建原始坐标x

由投影后降维坐标: $$z=U_{reduce}^{T}x$$可得：$$x_{approx}^{(1)}=U_{reduce}.z^{(1)}$$ 其中$U_{reduce}$为n x k矢量，$z^{(1)}$为k x 1矢量，数字表示样本序号

因此，如果已知z，可以反求原二维平面的坐标，但是这些坐标是近似的，落在PCA曲线上

选择PCA数字 - k

• 均方投影误差：$\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}-x_{approx}^{(i)}||$
• 数据总方差：$\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}||$
• K是满足$$\frac{\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}-x_{approx}^{(i)}||}{\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}||}<=0.01$$的最小值，阈值0.01并不是死定的，而是最常用的
  
  
  根据选取k的最小值原理，从1开始，循环增加检查满足阈值条件的最小值即可

另外，我们也可以使用PCA方程来检验k：

1. 计算PCA方程$$[U,S,V]=svd(Sigma)$$
2. 获得矩阵S
3. 计算$$1-\frac{{\sum }_{i=1}^k{S}_{ii}}{{\sum }_{i=1}^n{S}_{ii}}<=0.01$$同样k从1递增，选择满足阈值条件的最小值

使用PCA提高算法速度

使用PCA对交叉验证集和测试集的准确度几乎没有影响，但是能够显著提升算法速度

1. 提取样本输入集，进行数据分割
2. 使用且仅使用训练集运算PCA算法，获得投影所需的$K和U_{reduce}$
3. 将投影运用到交叉验证集和测试集，计算代价函数，获得评估误差值

使用PCA

• 压缩数据：减少磁盘和内存空间
• 增加算法运行速度
• 实现数据可视化（k=2/3）

莫使用PCA

• 用来避免过拟合（天才的想法，确实有效果，但是还是使用正则化为好）
• 开局获得数据就是用PCA
  你应该对原始数据公式使用正则化，规模缩放，特征增减等等数据处理措施仍达不到理想的结果或者速度的情况下，最后考虑使用PCA