SLAM库学习：从因子图到GTSAM

最新推荐文章于 2024-02-21 19:36:03 发布

MIKingZCC

最新推荐文章于 2024-02-21 19:36:03 发布

阅读量3.2k

点赞数 7

分类专栏：多传感器融合文章标签：概率论自动驾驶 slam 机器学习图优化

本文链接：https://blog.csdn.net/weixin_44156680/article/details/118784479

版权

多传感器融合专栏收录该内容

8 篇文章 32 订阅

订阅专栏

一、从贝叶斯网络到因子图优化

1. 贝叶斯网络

在这里插入图片描述
分析上图的贝叶斯网络，机器人状态 $x_0$ 、 $x_1$ 、 $x_2$ 、 $x_3$ 满足一阶马尔科夫性；空间中存在路标 $l_1$ 、 $l_2$ 、 $l_3$ ；而 $z_1$ 到 $z_8$ 分别代表了在机器人的各个状态对空间路标的测量值。所以整个贝叶斯网络的概率值可以表示为：
$P(X,L,Z)=P(x_0)\prod P(x_i|x_{i-1},u_i)\prod P(z_i|x_i,l_i)$
我们假设所有的状态变量和观测值都服从高斯分布，后验概率和似然概率可以表示如下：
在这里插入图片描述

2. 因子图

在贝叶斯网络中，测量值与状态量、路标一样是以节点的形式存在，这会给我们的分析带来一些不便。同时，我们发现贝叶斯网络中的最大后验概率由许多项因子乘积而成，所以我们引入了因子图，与贝叶斯网络对应的因子图表示如下：
在这里插入图片描述

与有向无环图不同（贝叶斯网络就是一种典型的有向无环图），因子图是一种无向图，由两种不同的节点组成：表示优化变量（在上图中体现为路标值和状态值）的变量因子以及表示因子（在上图中体现为路标值和状态值的测量值）的因子节点。

现在我们来考虑优化问题，在贝叶斯网络中，我们的目标是在既有的约束之上，通过调整随机变量的取值，使整个后验概率最大：
$x,l）^*=arg max (P(X,L,Z))$
因子图的概率正比与所有因子概率的乘积，所以同样的，对因子图的优化，就是调整各变量的值，使它们的因子之乘积最大化。
在这里插入图片描述
其中：

3. 非线性最小二乘问题

所以可以发现，无论是贝叶斯网络还是因子图，最后都是一个MAP（最大后验）问题：

在这里插入图片描述
对这一问题取负对数，即可得到最小二乘问题：

对于非线性最小二乘问题的解法在此不再赘述，SLAM常用的有L-M法、G-N法、置信域法等等。

考虑一个简单的因子图：
在这里插入图片描述
我们可以得到优化矩阵形式如下：

矩阵中的列表示每个待优化的变量，而每一行表示对应的测量值（因子），例如第一行则表示在 $x_1$ 状态看到的 $l_1$ 路标。在求解过程中，我们应该充分利用A的稀疏性，但是选取不同的优化变量和因子顺序，稀疏性不同，在GTSAM中会自动调整选取。

上面分析的方法在普通的向量空间中优化当然是可行的，其实在非平凡的空间中（李群和其他一般流形等等）GTSAM也可以有类似的操作。
李群（指数映射）：
在这里插入图片描述
一般的流形：

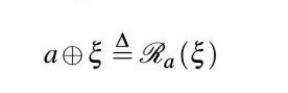
4. 线性最小二乘问题

其实在最后非线性最小二乘问题最后都化成了线性最小二乘问题，在GTSAM中提供了两种分解方法，考虑一个线性最小二乘问题：
在这里插入图片描述

(1) QR分解

QR分解又称正交三角分解，利用的其实就是施密特正交化。
对于一个列满秩的矩阵而言，正交化可以得到正交矩阵Q，利用Q可以得到上三角矩阵R，从而求解线性系统：
在这里插入图片描述

(2) Cholesky 分解

Cholesky分解法又叫平方根法，Cholesky分解把矩阵分解为一个下三角矩阵以及它的共轭转置矩阵的乘积（那实数界来类比的话，此分解就好像求平方根）。与一般的矩阵分解求解方程的方法比较，Cholesky分解效率很高（速度比QR一般要快一个数量级），但稳定性相对于QR分解而言比较差(稳定性通俗的讲就是在矩阵接近奇异（特征值接近0）时候时的求解)：

在这里插入图片描述

二、iSAM2和贝叶斯树

在进行普通的批量优化时，每次新的状态量加入都要对所有状态重新计算，这大大降低了SLAM的实时性，在GTSAM中ISAM2的作用就是在一定程度上解决这一问题，在每次有新的变量和因子加入时，首先分析它们和因子图之间的链接和影响关系，考虑之前存储的信息有哪些可以继续利用，哪些必须重新计算，从而实现"增量特性"。但是值得注意的是，当图的规模发生一定程度的改变时，做全图的优化是不可避免的。
ISAM2将因子图 $(a)$ 通过贝叶斯网络 $(b)$ 转换成贝叶斯树 $(c)$ ：
在这里插入图片描述
在下图中红色轨迹表示受到当前状态影响的先前状态，比较于全图优化，大大减少了计算量，但是在面对回环时，仍然需要进行较大面积的优化，具体的细节请参考iSAM2论文。

三、GTSAM实战

GTSAM提供了一份实例程序：
https://github.com/borglab/gtsam
https://github.com/dongjing3309/gtsam-examples

1. Pose2SLAMExample实例

在这里插入图片描述

(1) 建立因子图

创建因子图容器：

  // Create a factor graph container
  NonlinearFactorGraph graph;

添加先验因子：

  // Add a prior on the first  pose, setting it to the origin
  // The prior is needed to fix/align the whole trajectory at world frame
  // A prior factor consists of a mean value and a noise model (covariance matrix)
  noiseModel::Diagonal::shared_ptr priorModel = noiseModel::Diagonal::Sigmas(Vector3(1.0, 1.0, 0.1));
  graph.add(PriorFactor<Pose2>(Symbol('x', 1), Pose2(0, 0, 0), priorModel));

添加里程计因子：

  // odometry measurement noise model (covariance matrPose2GPSExampleix)
  noiseModel::Diagonal::shared_ptr odomModel = noiseModel::Diagonal::Sigmas(Vector3(0.5, 0.5, 0.1));
  // Add odometry factors
  // Create odometry (Between) factors between consecutive poses
  // robot makes 90 deg right turns at x3 - x5
  graph.add(BetweenFactor<Pose2>(Symbol('x', 1), Symbol('x', 2), Pose2(5, 0, 0), odomModel));
  graph.add(BetweenFactor<Pose2>(Symbol('x', 2), Symbol('x', 3), Pose2(5, 0, -M_PI_2), odomModel));
  graph.add(BetweenFactor<Pose2>(Symbol('x', 3), Symbol('x', 4), Pose2(5, 0, -M_PI_2), odomModel));
  graph.add(BetweenFactor<Pose2>(Symbol('x', 4), Symbol('x', 5), Pose2(5, 0, -M_PI_2), odomModel));

添加回环因子：

  // loop closure measurement noise model
  noiseModel::Diagonal::shared_ptr loopModel = noiseModel::Diagonal::Sigmas(Vector3(0.5, 0.5, 0.1));

  // Add the loop closure constraint
  graph.add(BetweenFactor<Pose2>(Symbol('x', 5), Symbol('x', 2), Pose2(5, 0, -M_PI_2), loopModel));
  
  // print factor graph
  graph.print("\nFactor Graph:\n");

(2) 添加初始值：

  // initial varible values for the optimization
  // add random noise from ground truth values
  Values initials;
  initials.insert(Symbol('x', 1), Pose2(0.2, -0.3, 0.2));
  initials.insert(Symbol('x', 2), Pose2(5.1, 0.3, -0.1));
  initials.insert(Symbol('x', 3), Pose2(9.9, -0.1, -M_PI_2 - 0.2));
  initials.insert(Symbol('x', 4), Pose2(10.2, -5.0, -M_PI + 0.1));
  initials.insert(Symbol('x', 5), Pose2(5.1, -5.1, M_PI_2 - 0.1));
  
  // print initial values
  initials.print("\nInitial Values:\n");

(3) 优化

创建优化方法：

  // Use Gauss-Newton method optimizes the initial values
  GaussNewtonParams parameters;

创建优化器并进行优化：

  // print per iteration
  parameters.setVerbosity("ERROR");
  
  // optimize!
  GaussNewtonOptimizer optimizer(graph, initials, parameters);
  Values results = optimizer.optimize();
  
  // print final values
  results.print("Final Result:\n");

(4) 完全后验推论

GTSAM在测量所有之后，也可以计算每个状态的协方差矩阵，由于因子图实际上表征的是后验概率 $P (X ∣ Z)$ ，所以每个姿态的均值 $μ$ 和协方差 $\sum$ 近似于边缘后验概率 $P (x ∣ Z)$ 。请注意，这只是一个近似，因为即使在这个简单的情况下，里程计因子实际上在它们的论据中是非线性的，而GTSAM只计算了真实的后验的高斯近似：

  // Calculate marginal covariances for all poses
  Marginals marginals(graph, results);
  
  // print marginal covariances
  cout << "x1 covariance:\n" << marginals.marginalCovariance(Symbol('x', 1)) << endl;
  cout << "x2 covariance:\n" << marginals.marginalCovariance(Symbol('x', 2)) << endl;
  cout << "x3 covariance:\n" << marginals.marginalCovariance(Symbol('x', 3)) << endl;
  cout << "x4 covariance:\n" << marginals.marginalCovariance(Symbol('x', 4)) << endl;
  cout << "x5 covariance:\n" << marginals.marginalCovariance(Symbol('x', 5)) << endl;

2. 添加自定义因子

在这里插入图片描述
在提供的示例中，GPSPose2Factor.h实现了自定义添加一个GPS因子，如上图所示。

定义一个GPS类，由于GPS因子属于一元因子，所以继承自gtsam::NoiseModelFactor1。当然，若是自定义二元因子时，继承的类为gtsam::NoiseModelFactor1。模板参数为状态量的类型，此处gtsam::Pose2代表SE2：

class GPSPose2Factor: public gtsam::NoiseModelFactor1<gtsam::Pose2> {

(1) 定义自定义因子类的私有成员变量

私有数据一般指测量值：

private:
  // measurement information
  double mx_, my_;

(2) 定义自定义因子类的公共成员函数

自定义因子类的构造函数：

public:

  GPSPose2Factor(gtsam::Key poseKey, const gtsam::Point2 m, gtsam::SharedNoiseModel model) :
      gtsam::NoiseModelFactor1<gtsam::Pose2>(model, poseKey), mx_(m.x()), my_(m.y()) {}

定义误差模型、求解雅可比矩阵：

  gtsam::Vector evaluateError(const gtsam::Pose2& p, boost::optional<gtsam::Matrix&> H = boost::none) const {
  
    // note that use boost optional like a pointer
    // only calculate jacobian matrix when non-null pointer exists
    if (H) *H = (gtsam::Matrix23() << 1.0, 0.0, 0.0, 
                                      0.0, 1.0, 0.0).finished();
    
    // return error vector
    return (gtsam::Vector2() << p.x() - mx_, p.y() - my_).finished();
  }

(3) 自定义因子的使用

graph.add(GPSPose2Factor(Symbol('x', 1), Point2(0, 0), gpsModel));

3. 自动求导的使用

我们仍然以上面自定义的GPS因子为例，首先建立正常的损失函数，在调用时有些许的不同。

(1) 建立损失函数

定义：

gtsam::Point2 projectPose2(const gtsam::Pose2& pose, 
    gtsam::OptionalJacobian<2,3> H = boost::none);

实现：

gtsam::Point2 projectPose2(const gtsam::Pose2& pose, gtsam::OptionalJacobian<2,3> H) {
  
  // jacobian: left 2x2 identity + right 2x1 zero 
  if (H) *H = (gtsam::Matrix23() << 1.0, 0.0, 0.0, 
                                    0.0, 1.0, 0.0).finished();
  
  // return translation
  return gtsam::Point2(pose.x(), pose.y());
}

(2) 自动求导因子的使用

在使用时添加的是表达式因子，第一个参数为之前定义的损失函数（参数为状态对应的key），第二个参数为初始值，第三个参数为噪声。

graph.addExpressionFactor(projectPose2_(x1_), Point2(0, 0), gpsModel);

4. iSAM2的使用

(1) iSAM2优化参数

  ISAM2Params parameters;
  parameters.relinearizeThreshold=0.01;      //差值大于0.1需要重新线性化
  parameters.relinearizeSkip=1;             //每当有1个值需要重新线性化时，对贝叶斯树进行更新
  parameters.enableRelinearization=true;    //是否可以重新线性化任意变量
  parameters.evaluateNonlinearError=false;  //是否计算线性化误差默认false
  parameters.cacheLinearizedFactors = false;  //default: true 是否保存保存线性化结果，可以优化性能，但是当线性化容易计算时会造成相反效果
  parameters.factorization=ISAM2Params::Factorization::QR;//默认为QR分级，还可以选用CHOESKY分解，但CHOESKY求解数值不稳定
  parameters.keyFormatter=DefaultKeyFormatter;//  debug时key值形式默认
  parameters.enableDetailedResults=true;     //是否计算返回ISAM2Result::detailedResults，会增加计算量
  parameters.enablePartialRelinearizationCheck=false; //是否只进行部分更新功能
  parameters.findUnusedFactorSlots=false;//当要移除许多因子时，比如ISAM2做固定平滑时，启用此选项第一值进行插入时
                                          //避免出现NULL值，但是会造成每当有新值插入时必须查找

(2) iSAM2建立贝叶斯树

  ISAM2 isam(parameters);//贝叶斯树
  NonlinearFactorGraph graph;
  Values initialEstimate;

(3) iSAM2更新

使用update函数，参数分别为图结构和初值。

ISAM2Result result=isam.update(graph,initialEstimate);

(4) iSAM2求解

Values currentEstimate=isam.calculateBestEstimate();//calculateBestEstimate使用所有值进行回带

MIKingZCC

关注

7
点赞
踩
84

收藏

觉得还不错? 一键收藏
0
评论
SLAM库学习：从因子图到GTSAM

SLAM库学习：从因子图到GTSAM一、从贝叶斯网络到因子图优化1. 贝叶斯网络2. 因子图3. 非线性最小二乘问题4. 线性最小二乘问题(1) QR分解(2) Cholesky 分解二、iSAM2三、GTSAM实战一、从贝叶斯网络到因子图优化1. 贝叶斯网络分析上图的贝叶斯网络，机器人状态x0x_0x0、x1x_1x1、x2x_2x2、x3x_3x3满足一阶马尔科夫性；空间中存在路标l1l_1l1、l2l_2l2、l3l_3l3；而z1z_1z1到z8z_8z8分别代表了在机器
复制链接

扫一扫