傅里叶级数在三角插值多项式中的应用（含例题）

傅里叶级数在三角插值多项式中的应用

理论部分
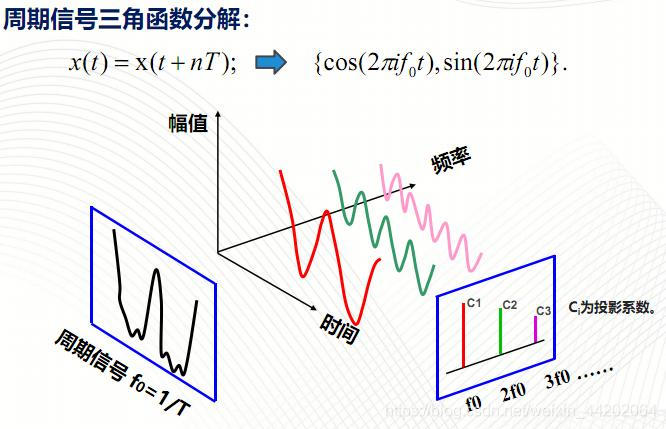
用正弦和余弦函数表示任意函数始于18世纪50年代。下面介绍最佳平方三角逼近多项式和傅立叶级数。


例题部分
使用傅里叶变换确定函数f(x)=x^2*cos(x)在[-pi,pi]上的16次三角插值多项式。
（1）编写子程序fseries.m，求傅里叶系数及级数。程序如下：
% 功能：求解函数的傅里叶系数及傅里叶级数。 %an，bn为傅里叶系数，f为傅里叶多项式；
%fx为函数，x为自变量，n为三角多项式的次数，a,b为函数fx的定义域

function [an,bn,f]=fseries(fx,x,n,a,b)
if nargin==3
a=-pi;
b=pi;
end
l=(b-a)/2;
if a+b
fx=subs(fx