【Comsol学习】一维传热问题仿真

回顾之前自己做的练习，发现还是做的太过浅薄，因此打算从头进行学习，首先先从最简单的一维传热问题仿真开始，后续随着学习希望能够自己能够进行一些传热和流体上的分析，加深对模型的理解。

 

问题分析

模型域定义在x=-b与x=b之间。整个域上的初始温度恒定，等于T0；参见下图。在 t=0时，两个边界处的温度下降到T1。

引入一些无量纲变量来方便计算

代入新的无量纲变量，控制方程和边界条件变为：

对于边界处的温度下降，可以使用一个阶跃函数来模拟壁温突变的扰动，温度变化后保持恒壁温条件。

 

---

建模仿真

 

为了求解传热问题的数值解，我们需要控制方程、物理条件、几何条件、边界条件、初始条件，并对计算域进行离散化，我们按照comsol的逻辑来进行操作：

 

第一类边界条件情况下的变化

几何条件

建立一个x在(-1,1)的线段

 

物理条件

设置计算域的导热系数、密度、恒压热容 

 

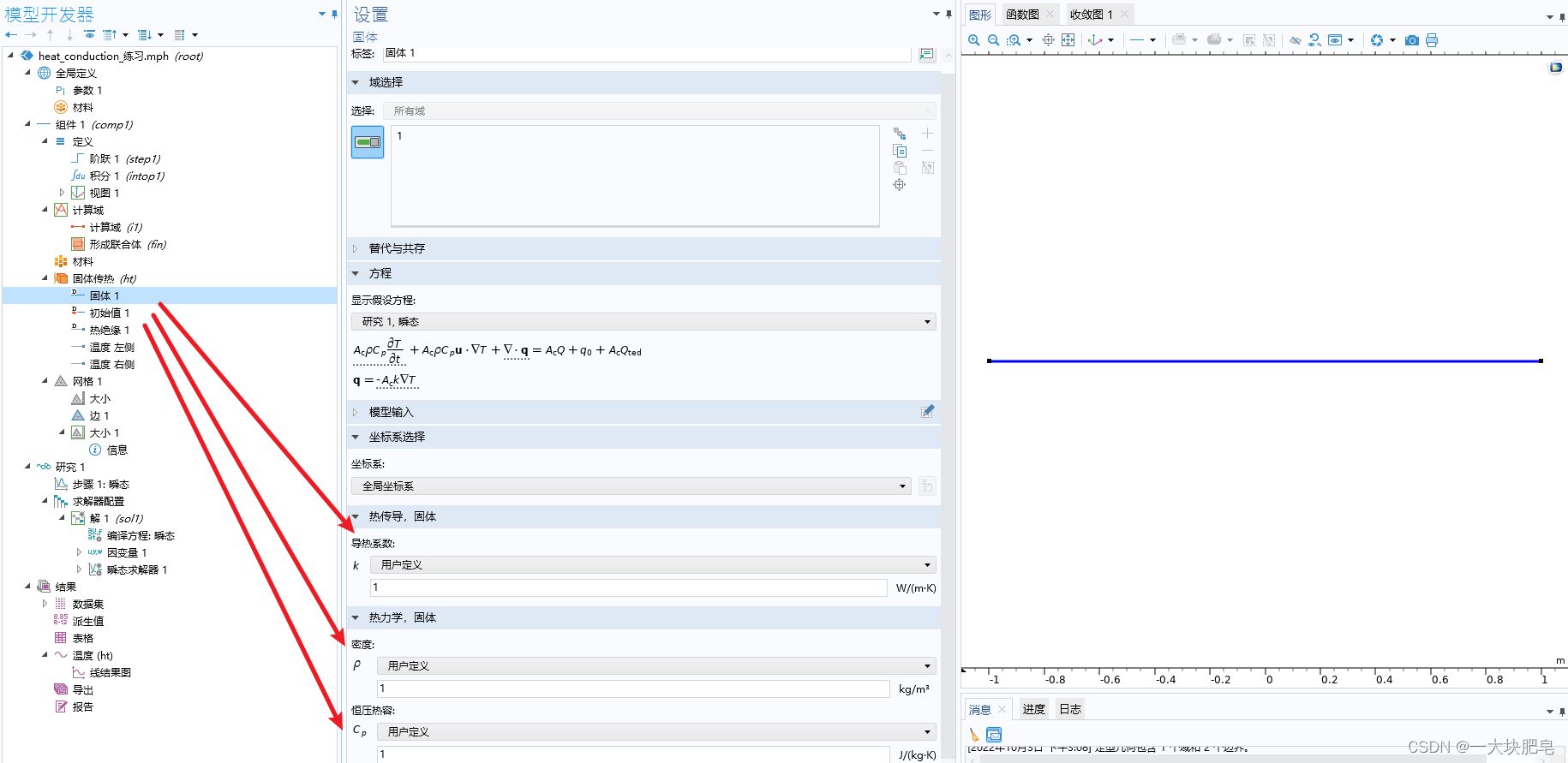
 边界条件

创建一个局部阶跃函数，准备添加为边界条件

将阶跃step1(t)设置为两个边界节点的温度

 

初始条件

设置计算域初始值

 

网格划分

主体区域进行简单的网格划分

对边界再进行划分

 

求解

按照例程设置瞬态求解器

 

解的可视化和分析

选择需要显示的时间结果

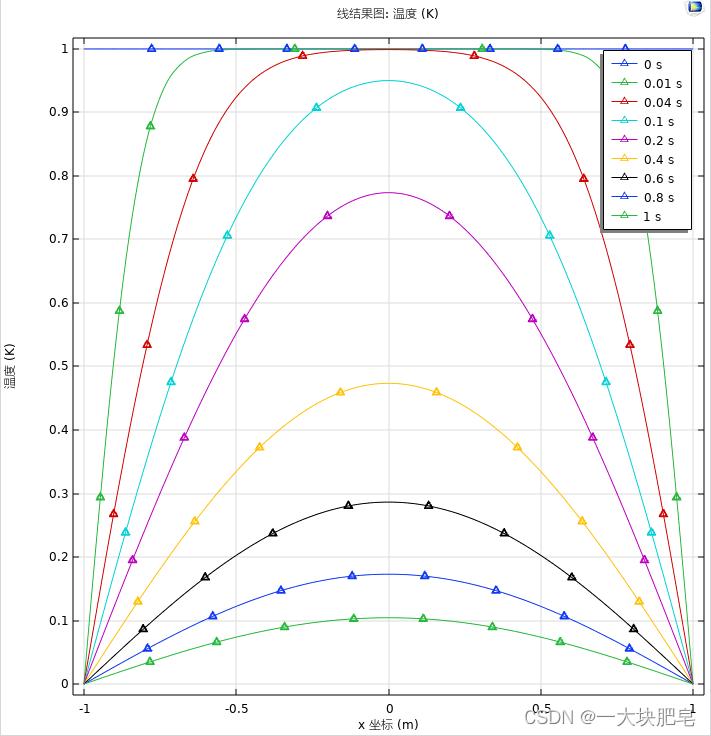
对温度分布曲线进行可视化，选择图例、图线等样式

可以看到随着时间的增长，温度逐渐沿抛物线逐渐下降，内部温度逐渐扯平。

 

---

求解器设置调整测试

用最简单的求解器配置好像也和前面按教程设置也没啥问题

 

---

第二类边界条件情况下的变化

变更边界条件为恒热流边界条件，再次进行求解

 

 

---

第三类边界条件情况下的变化

尝试设置第三类边界条件求解

comsol中的边界条件怎么选择？ - 知乎

 

根据comsol的知乎答案，comsol可以通过增加面外热通量的物理场来设置第三类边界条件。如下可以添加对流热通量和核沸腾热通量：

 

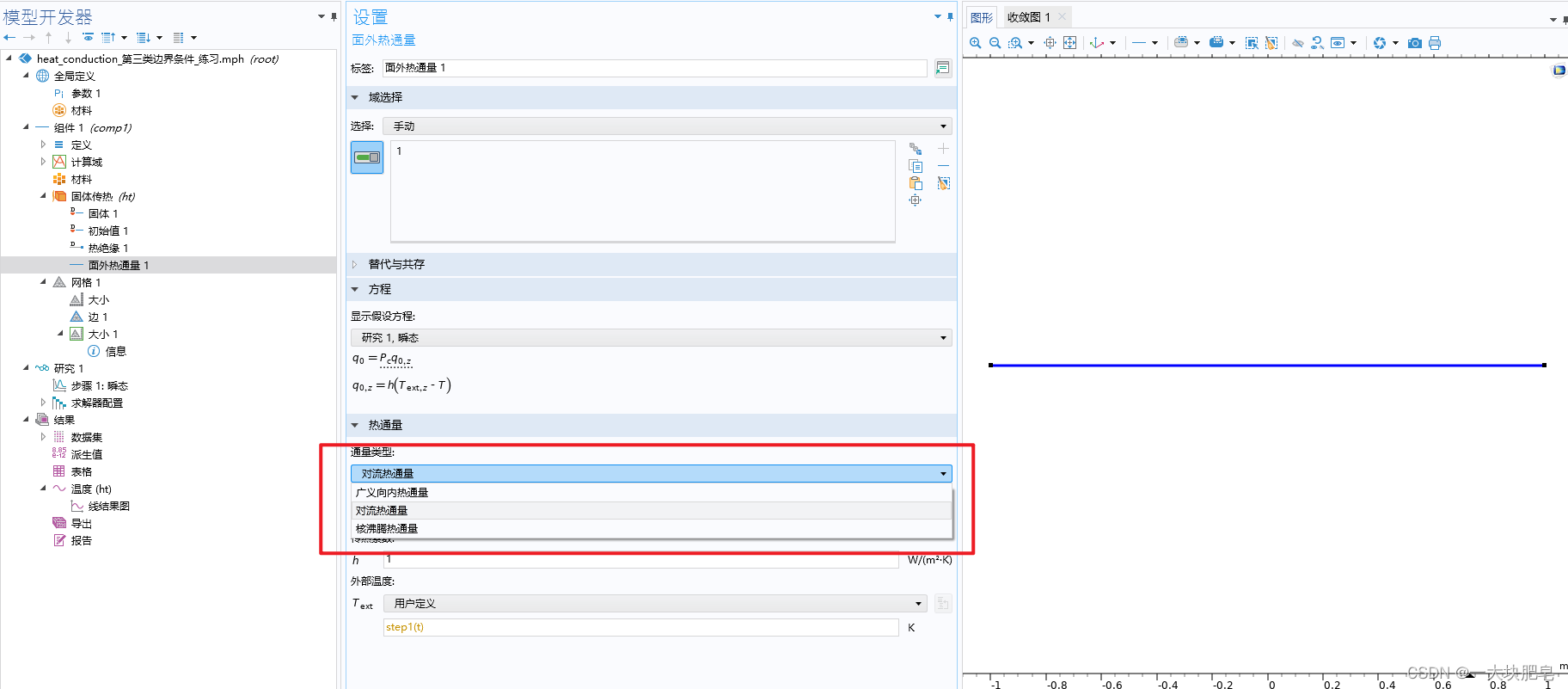
可是仿真结果看来这个面外热通量应该是施加在整个一维计算域上的，而非两侧的边界

 

如何对两侧点设置第三类边界条件？目前这个问题还未找到答案