基于MPTA+弱磁控制(直接计算法)+电流解耦器PMSM系统simulink实现
总体控制框图
:

其中控制算法的流程:
 首先我们说一下电流极限圆和电压极限圆的概念及其公式:
首先我们说一下电流极限圆和电压极限圆的概念及其公式:
1、电压极限圆

带入得到:

2、电流极限圆
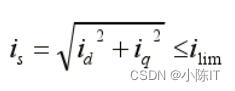
当电机处于稳定状态时,将电压约束方程和电流约束方程画在 id、iq 平面上,如图所示:
 当考虑定子电阻的影响以后,在给定转速下,输出转矩的能力有所下降;在给定转矩下,能达到的最大转速也有所降低;因此在转速较高时,将电阻的影响忽略不计(上图就是不考虑定子电阻的影响)。
当考虑定子电阻的影响以后,在给定转速下,输出转矩的能力有所下降;在给定转矩下,能达到的最大转速也有所降低;因此在转速较高时,将电阻的影响忽略不计(上图就是不考虑定子电阻的影响)。
二、弱磁控制的三个区域

区域 1:PMSM 在该区域的转速小于转折速度,此区域由于还未进行弱
磁,输出为恒转矩,所以区域 1 也成为恒转矩运行区。为了充分利用电机的输出能力,在此区间常采用 MTPA 控制方式。
区域 2:该区域为一般弱磁区,PMSM 的转速大于转折速度,为什么此时
不再使用 MTPA 而要用特定的弱磁策略呢,如下图所示,

当电机的 idiq 特性处于 MTPA 曲线时,假设升速到 BC 所在的电压极限
圆,此时 B 点和 C 点的电磁转矩输出能力明显不同,C 点的电磁转矩输出能力明显大于 B 点的电磁转矩输出能力。如果还是按照 MTPA 曲线去给定 d 轴电流,就会导致电机的输出能力下降,所以需要使用 C 点的 idiq 特性。
定子电流分量按照下式求得:
 可以得到 id 的运行轨迹为:
可以得到 id 的运行轨迹为:

上图所示的关系式,是通过电压极限圆和电流极限圆的交点所得,电机的
定子电流轨迹沿着电流极限圆和电压极限圆的交点运行,且幅值始终保持为 Ilim
区域 3:区域 3 也成为深度弱磁区和弱磁 2 区,不是所有的电机都存在区
域 3,只有当 lim / f d L I 的时候才会存在,这个关系的不同可以反映在电压极限圆和电流极限圆的坐标系中。


所以可以看到弱磁的曲线也是不一样的。
电机在该区域运行时,定子电流分量 id 和 iq 可以按照下式求得:

三、slimulink仿真控制

3.1给定转速


3.2转速环PI
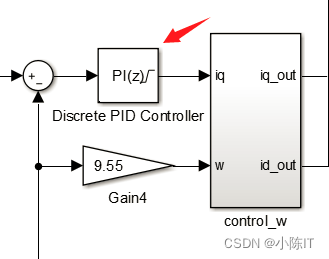

3.3控制算法(MPTA+弱磁)

其中内部结构为

其中MPTA内部为:

其中弱磁控制(flux-weaking)内部为:

3.4电流环PI


3.5解耦电流控制器代码
function [ud_out,uq_out] = fcn(ud,uq,id,iq,we,pisa,Ld,Lq)
ud_out=ud-iq*we*Lq;
uq_out=uq+id*we*Ld+we*pisa;
end
3.5逆变器参数

3.6三相电压电流测量模块

3.7电机参数



3.8转速波形
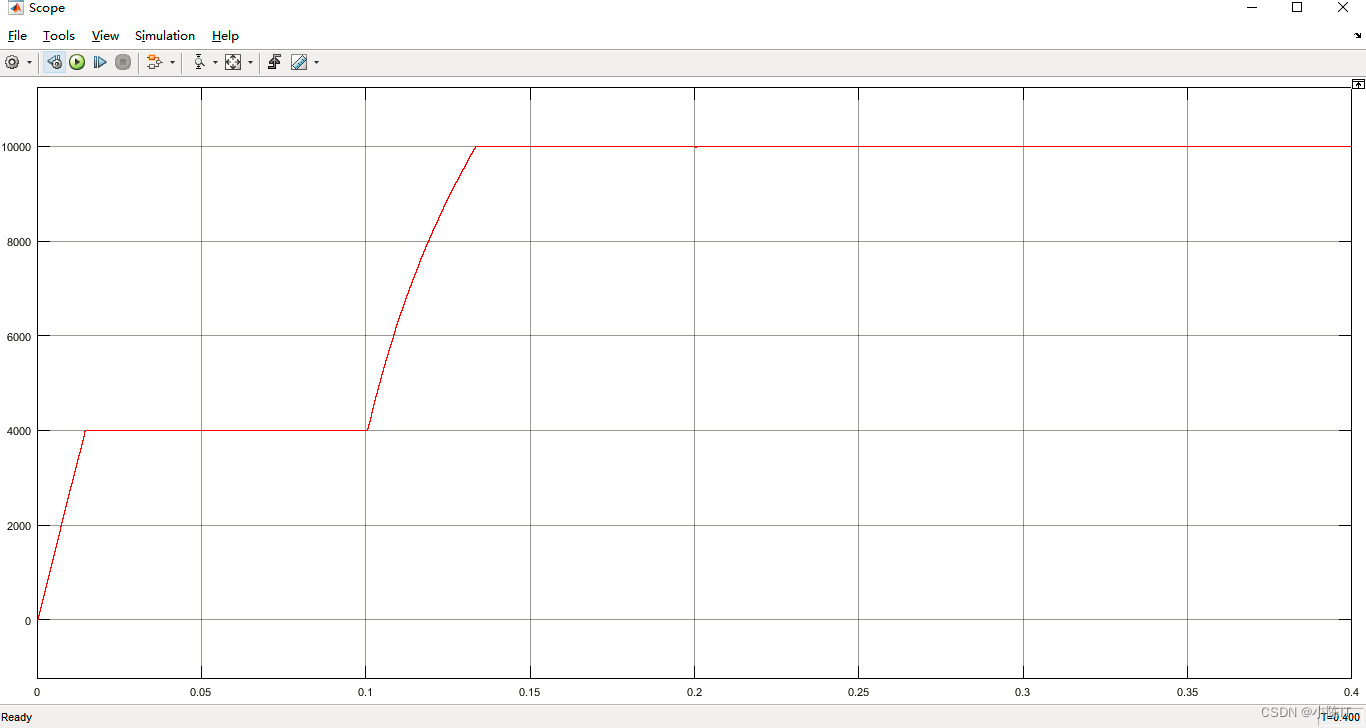
3.9转矩波形
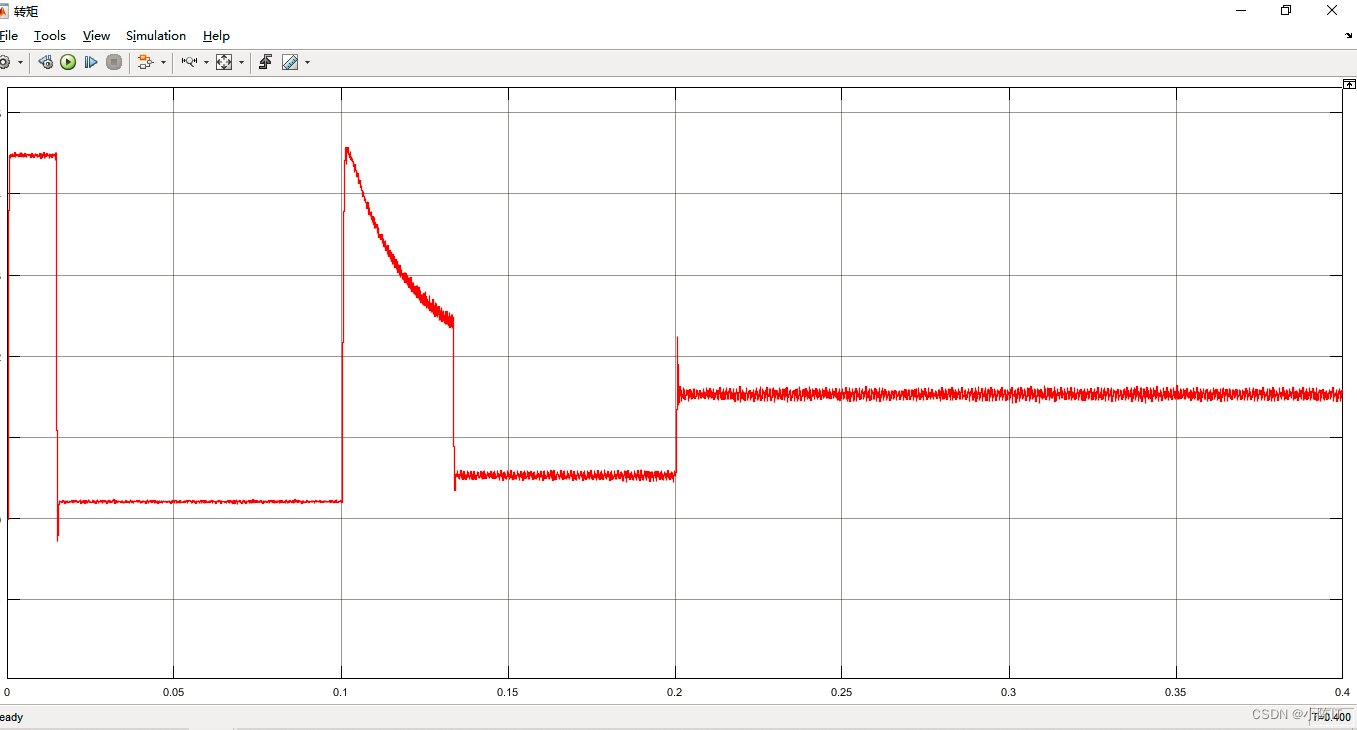























 786
786

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








