卷积和
连续是卷积积分。
1 序列的时域分解
任意离散序列 f ( k ) f(k) f(k)可表示为
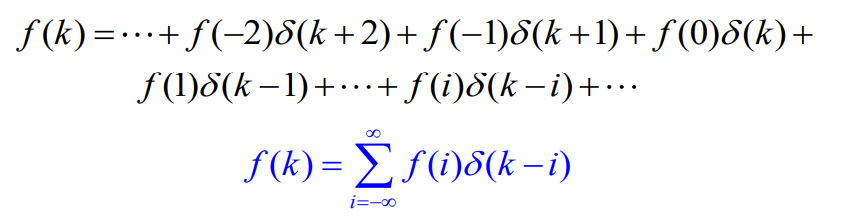
2 任意离散信号作用下的零状态响应
3 卷积和公式
卷积和的定义
已知定义在区间
(
–
∞
，
∞
)
(–∞，∞)
(–∞，∞) 上的两个函数
f
1
(
k
)
f_1(k)
f1(k)和
f
2
(
k
)
f_2(k)
f2(k)，则定义
为
f
1
(
k
)
f_1(k)
f1(k)与
f
2
(
k
)
f_2(k)
f2(k)的卷积和，简称卷积；记为
注意：求和是在虚设的变量 i i i 下进行的， i i i 为求和变量， k k k 为参变量。结果仍为 k k k 的函数。
若有两个序列
f
1
(
k
)
f_1(k)
f1(k)与
f
2
(
k
)
f_2(k)
f2(k)，如果序列
f
1
(
k
)
f1(k)
f1(k)是因果序列，即有
f
1
(
k
)
=
0
,
k
<
0
f_1(k)=0, k<0
f1(k)=0,k<0, 则卷积和可改写为：
若有两个序列
f
1
(
k
)
f_1(k)
f1(k)与
f
2
(
k
)
f_2(k)
f2(k)，如果序列
f
2
(
k
)
f_2(k)
f2(k)是因果序列，即有
f
2
(
k
)
=
0
,
k
<
0
f_2(k)=0, k<0
f2(k)=0,k<0, 则卷积和可改写为：
如果序列
f
1
(
k
)
f_1(k)
f1(k)与
f
2
(
k
)
f_2(k)
f2(k)均为因果序列，即若
f
1
(
k
)
=
f
2
(
k
)
=
0
,
k
<
0
f_1(k)=f_2(k)=0,k<0
f1(k)=f2(k)=0,k<0, 则卷积和可写为：
ε
(
k
)
：
k
>
0
\varepsilon(k)：k>0
ε(k)：k>0
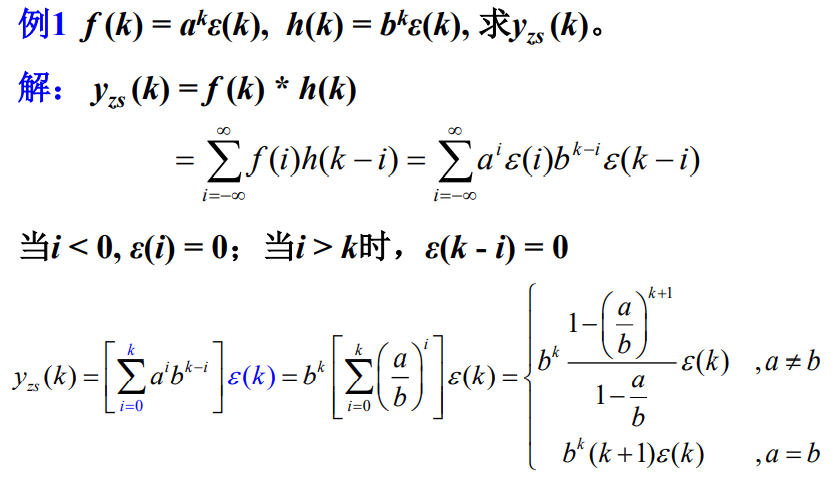
4 卷积和的图解法
注意： k k k 为参变量。
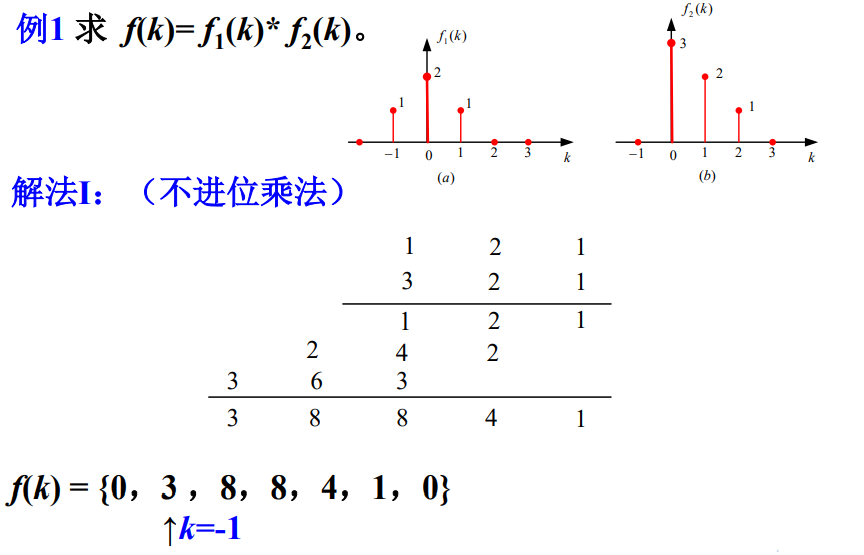
5 卷积和的不进位乘法运算
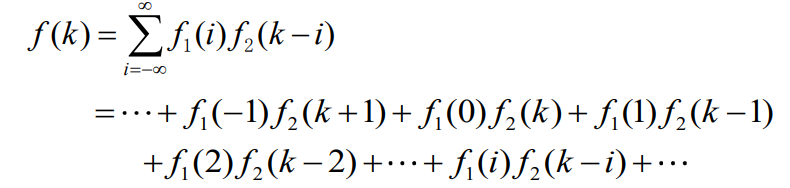
f
(
k
)
=
f(k)=
f(k)=所有两序列序号之和为
k
k
k的那些样本乘积之和。
f 1 ( 1 ) f 2 ( 0 ) ： k = 0 + 1 f_1(1)f_2(0)：k=0+1 f1(1)f2(0)：k=0+1
f 1 ( 1 ) f 2 ( 1 ) + f 1 ( 2 ) f 2 ( 0 ) ： k = 1 + 1 = 2 + 0 = 2 f_1(1)f_2(1)+f_1(2)f_2(0)：k=1+1=2+0=2 f1(1)f2(1)+f1(2)f2(0)：k=1+1=2+0=2
f 1 ( 2 ) f 2 ( 1 ) + f 1 ( 3 ) f 2 ( 0 ) ： k = 2 + 1 = 3 + 0 = 3 f_1(2)f_2(1)+f_1(3)f_2(0)：k=2+1=3+0=3 f1(2)f2(1)+f1(3)f2(0)：k=2+1=3+0=3
f 1 ( 3 ) f 2 ( 1 ) ： k = 3 + 1 f_1(3)f_2(1)：k=3+1 f1(3)f2(1)：k=3+1
2 × 3 = 6 ： k = 1 + 0 = 1 2\times 3=6：k=1+0=1 2×3=6：k=1+0=1
6 卷积和的性质
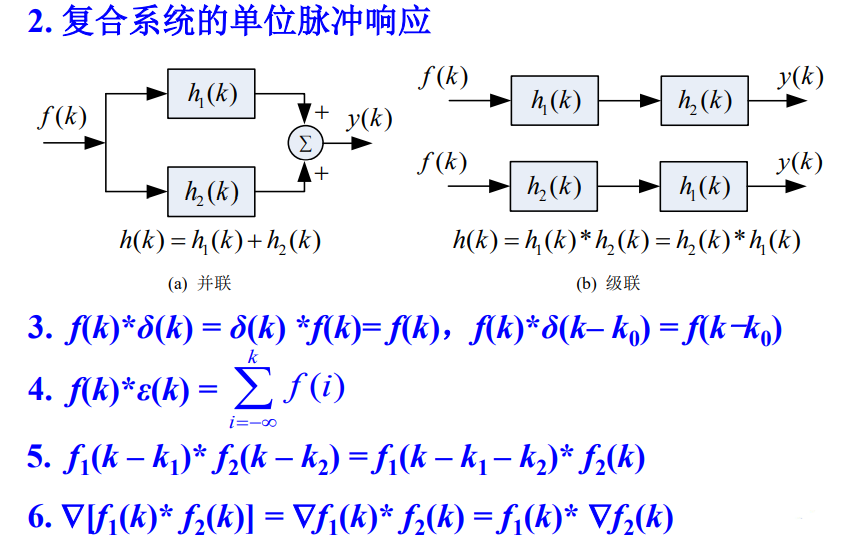
常用卷积和公式
《工程信号与系统》作者：郭宝龙等
国家精品课程：信号与系统 ，中国大学MOOC，郭宝龙，朱娟娟
扫一扫
1307
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
