文章目录

2 线性代数(Linear Algebra)(上)
在形式化一些直观概念时,常见的方法是构造一组对象(符号)和一些操作这些对象的规则。这就是所谓的代数(algebra)。线性代数是研究向量以及使用某些确定的规则来操作向量的一门学科。
我们许多人从学校里知道的向量被称为“几何向量”,通常用上方带一个小箭头的字母表示,例如 y ⃗ \vec{y} y 和 x ⃗ \vec{x} x。在这本书中,我们将讨论向量的更一般的概念,并使用粗体字母来表示它们,例如, x \boldsymbol{x} x和 y \boldsymbol{y} y
一般来说,向量是特殊的对象,将它们相加并乘以标量产生的是另一个相同类型的对象。从抽象的数学来看,任何满足这两个性质的物体都可以被认为是向量。下面举一些例子:

图 2.1 不同类型的向量。向量可以是出人意料的对象,包括(a)几何向量和(b)多项式。
1 几何向量
几何向量(见图2.1(a))在高中数学和物理中可能很常见。它可以被绘制成有向线段(至少二维)。两个几何向量 x → \overrightarrow{\boldsymbol{x}} x 和 y → \overrightarrow{\boldsymbol{y}} y相加: x → + y → = z → \overrightarrow{\boldsymbol{x}}+\overrightarrow{\boldsymbol{y}}=\overrightarrow{\boldsymbol{z}} x+y=z,得到另一几何向量 z → \overrightarrow{\boldsymbol{z}} z。另外,几何向量与一个标量(scalar)相乘: λ x → , λ ∈ R \lambda \overrightarrow{\boldsymbol{x}}, \lambda \in \mathbb{R} λx,λ∈R,依然得到一个几何向量。事实上, x → \overrightarrow{\boldsymbol{x}} x是被 λ λ λ缩放(scaled)的原始向量。因此,几何向量是前面介绍的向量概念的一个实例。将向量解释为几何向量使我们能够利用方向和大小直观地解释数学运算。
2 多项式
多项式也是向量;见图2.1(b):两个多项式能相加,并得到另一个多项式;多项式与标量 λ ∈ R \lambda \in \mathbb{R} λ∈R相乘,得到的也是多项式。因此,多项式也是向量的一个实例。注意多项式与几何向量有很大的不同。几何向量是具体的“图”,多项式是抽象的概念。然而,根据前文描述的向量概念,它们都是向量。
3 音频信号
音频信号是用一组数字表示的。我们可以把音频信号加在一起,得到新的音频信号。如果我们对音频信号进行缩放,我们也会得到一个音频信号。因此,音频信号也是向量。
4 R n \mathbb{R}^{n} Rn的元素(含 n n n个实数的元组)
R
n
\mathbb{R}^{n}
Rn比多项式更抽象,它是这本书关注的概念。例如,
a
=
[
1
2
3
]
∈
R
3
\boldsymbol{a}=\left[\begin{array}{l}1 \\2 \\3\end{array}\right] \in \mathbb{R}^{3}
a=
123
∈R3
这个向量包含三个实数元素。两个向量 a , b ∈ R n \boldsymbol{a}, \boldsymbol{b} \in \mathbb{R}^{n} a,b∈Rn相加得到另一个向量: a + b = c ∈ R n \boldsymbol{a}+\boldsymbol{b}=\boldsymbol{c} \in \mathbb{R}^{n} a+b=c∈Rn。另外,向量 a ∈ R n \boldsymbol{a} \in \mathbb{R}^{n} a∈Rn与标量 λ ∈ R \lambda \in \mathbb{R} λ∈R相乘得到一个被缩放的向量: λ a ∈ R n \lambda \boldsymbol{a} \in \mathbb{R}^{n} λa∈Rn。
将向量视为 R n \mathbb{R}^{n} Rn的元素还有一个额外的好处,即它可以用计算机上的实数数组表示。许多编程语言都支持数组操作,这使得我们可以方便地实现有关向量操作的算法。
线性代数关注的是这些向量之间的相似性。我们可以把它们加起来,然后乘以标量。我们将主要关注 R n \mathbb{R}^n Rn中的向量,因为线性代数中的大多数算法都是在 R n \mathbb{R}^n Rn中表述的。我们将在第8章中看到,我们用 R n \mathbb{R}^n Rn中的向量来表示数据。在这本书中,我们将关注有限维向量空间,在这种情况下,任何向量和 R n \mathbb{R}^n Rn之间都有1:1的对应关系。如果方便的话,我们将利用几何向量来直观表示,并考虑基于数组的算法。
数学中的一个主要概念是“封闭性”。相关的问题是:我提出的操作得到的所有的东西组成的集合是什么?在向量的例子中:从一个小的向量集合开始,然后把它们相加,再按比例缩放,得到的向量集合是什么?这将产生一个向量空间(第2.4节)。向量空间的概念及其特性是机器学习的基础。图2.2总结了本章介绍的概念。

图2.2 本章介绍的概念的思维导图,以及这些概念在本书其他部分中的使用。
线性代数在机器学习和一般数学中扮演着重要的角色。本章所介绍的概念将在第三章中进一步扩展到几何学相关的概念。在第五章,我们将讨论向量微积分,需要一些矩阵运算的知识。在第十章中,我们将使用投影(将在3.8节中介绍)进行主成分分析(PCA)实现降维。在第九章,我们将讨论线性回归,其中线性代数在解决最小二乘问题中扮演核心角色。
2.1 线性方程组
线性方程组是线性代数的核心部分。许多问题可以表述为线性方程组,而线性代数为我们提供了求解它们的工具。
例 2.1
一家公司要生产产品
N
1
,
…
,
N
n
N_{1}, \ldots, N_{n}
N1,…,Nn,需要资源
R
1
,
…
,
R
m
R_{1}, \ldots, R_{m}
R1,…,Rm。要生产单位产品
N
j
N_j
Nj,需要
a
i
j
a_{ij}
aij单位的资源
R
i
R_i
Ri。其中
i
=
1
,
…
,
m
i=1, \ldots, m
i=1,…,m,
j
=
1
,
…
,
n
j=1, \ldots, n
j=1,…,n
我们的目标是找到一个最优的生产计划,即在资源 R i R_i Ri的有单位总数 b i b_i bi可用且(理想情况下)没有剩余资源的前提下,产品 N j N_j Nj的应生产多少单位 x i x_i xi的计划。
如果我们要分别生产
x
1
,
…
,
x
n
x_{1}, \ldots, x_{n}
x1,…,xn单元个相应产品,我们总共需要
a
i
1
x
1
+
⋯
+
a
i
n
x
n
a_{i 1} x_{1}+\cdots+a_{i n} x_{n}
ai1x1+⋯+ainxn
单元个
R
i
R_i
Ri。最优生产计划
(
x
1
,
…
,
x
n
)
∈
R
n
\left(x_{1}, \ldots, x_{n}\right) \in \mathbb{R}^{n}
(x1,…,xn)∈Rn需要满足以下方程组:
a
11
x
1
+
⋯
+
a
1
n
x
n
=
b
1
⋮
a
m
1
x
1
+
⋯
+
a
m
n
x
n
=
b
m
(
2.3
)
\begin{array}{c}a_{11} x_{1}+\cdots+a_{1 n} x_{n}=b_{1} \\\vdots \\a_{m 1} x_{1}+\cdots+a_{m n} x_{n}=b_{m}\end{array} \qquad(2.3)
a11x1+⋯+a1nxn=b1⋮am1x1+⋯+amnxn=bm(2.3)
其中 a i j ∈ R a_{i j} \in \mathbb{R} aij∈R, b i ∈ R b_{i} \in \mathbb{R} bi∈R。
式(2.3)就是线性方程组(system of linear equations)的一般形式。 x 1 , … , x n x_{1}, \ldots, x_{n} x1,…,xn是这个方程组的未知数。每一个满足式(2.3)的 n n n元组 ( x 1 , … , x n ) ∈ R n \left(x_{1}, \ldots, x_{n}\right) \in\mathbb{R}^{n} (x1,…,xn)∈Rn都是线性方程组的一个解(solution)。
例 2.2
线性方程组
x
1
+
x
2
+
x
3
=
3
(
1
)
x
1
−
x
2
+
2
x
3
=
2
(
2
)
2
x
1
+
3
x
3
=
1
(
3
)
\begin{array}{rrr}x_{1}& +&x_{2}&+&x_{3}&=&3 \qquad(1)\\x_{1}& -&x_{2}&+&2 x_{3}&=&2 \qquad(2)\\2 x_{1}& & &+&3 x_{3}&=&1 \qquad(3)\end{array}
x1x12x1+−x2x2+++x32x33x3===3(1)2(2)1(3)
无解(no solution):将前两个方程相加得到 2 x 1 + 3 x 3 = 5 2 x_{1}+3 x_{3}=5 2x1+3x3=5,这与第三个方程(3)相矛盾。
让我们看看另一个线性方程组:
x
1
+
x
2
+
x
3
=
3
(
1
)
x
1
−
x
2
+
2
x
3
=
2
(
2
)
x
2
+
x
3
=
2
(
3
)
\begin{array}{rrr}x_{1}& +&x_{2}&+&x_{3}&=&3 \qquad(1)\\x_{1}& -&x_{2}&+&2 x_{3}&=&2 \qquad(2)\\& & x_{2}&+& x_{3}&=&2 \qquad(3)\end{array}
x1x1+−x2x2x2+++x32x3x3===3(1)2(2)2(3)
根据第一个和第三个方程,得到 x 1 = 1 x_1=1 x1=1。 由(1)+(2)得到: 2 x 1 + 3 x 3 = 5 2 x_{1}+3 x_{3}=5 2x1+3x3=5,即: x 3 x_3 x3=1。由(3),我们可以得到 x 2 = 1 x_2=1 x2=1。因此, ( 1 , 1 , 1 ) (1,1,1) (1,1,1)是唯一解(unique solution)(通过代入方程组可验证 ( 1 , 1 , 1 ) (1,1,1) (1,1,1)是解)。
接下来看第三个例子:
x
1
+
x
2
+
x
3
=
3
(
1
)
x
1
−
x
2
+
2
x
3
=
2
(
2
)
2
x
1
+
3
x
3
=
5
(
3
)
\begin{array}{rrr}x_{1}& +&x_{2}&+&x_{3}&=&3 \qquad(1)\\x_{1}& -&x_{2}&+&2 x_{3}&=&2 \qquad(2)\\2 x_{1}& & &+&3 x_{3}&=&5 \qquad(3)\end{array}
x1x12x1+−x2x2+++x32x33x3===3(1)2(2)5(3)
因为 ( 1 ) + ( 2 ) = ( 3 ) (1)+(2)=(3) (1)+(2)=(3),我们可以省略第三个等式(冗余)。由(1)和(2),我们可以得到: 2 x 1 = 5 − 3 x 3 2 x_{1}=5-3 x_{3} 2x1=5−3x3, 2 x 2 = 1 + x 3 2 x_{2}=1+x_{3} 2x2=1+x3。我们定义 x 3 = a ∈ R x_{3}=a \in \mathbb{R} x3=a∈R为自由变量,使得任意三元组 ( 5 2 − 3 2 a , 1 2 + 1 2 a , a ) , a ∈ R \left(\frac{5}{2}-\frac{3}{2} a, \frac{1}{2}+\frac{1}{2} a, a\right), \quad a \in \mathbb{R} (25−23a,21+21a,a),a∈R是线性方程组的一个解,即我们得到一个包含无穷多解(infinitely many solutions)的解集。
一般来说,对于一个实值线性方程组,我们要么无解,要么有唯一解,要么有无穷多解。线性回归(Linear regression,第九章)能解决无解的方程组。
备注(线性方程组的几何解释)。
在具有两个变量
x
1
x_1
x1,
x
2
x_2
x2的线性方程组中,每个线性方程表示
x
1
−
x
2
x_1-x_2
x1−x2平面上的一条线。由于线性方程组的解必须同时满足所有方程,所以解集是这些线的交集。这个交集可以是一条直线(如果线性方程描述同一条直线)、一个点,也可以是空的(当直线平行时)。
对于两个变量的方程组
4 x 1 + 4 x 2 = 5 2 x 1 − 4 x 2 = 1 \begin{array}{l}4 x_{1}+4 x_{2}=5 \\2 x_{1}-4 x_{2}=1\end{array} 4x1+4x2=52x1−4x2=1
其图示为:

图 2.3 二元线性方程组的解空间可以几何地解释为两条直线的交点。每个线性方程都代表一条直线。
方程组的解空间为点 ( x 1 , x 2 ) = ( 1 , 1 4 ) (x_1,x_2)=(1,\frac{1}{4}) (x1,x2)=(1,41)
类似地,对于三个变量,每个线性方程确定了三维空间中的一个平面。这些平面相交部分,即同时满足所有线性方程组的集合,为方程组的解集,它可以是一个平面、一条直线、一个点或空的(当这些平面不相交时)。
在介绍求解线性方程组的方法前,我们首先介绍一种线性方程组的紧凑表示法。我们将系数
a
i
j
a_{ij}
aij组合表示为向量,并进一步组合表示成矩阵。换句话说,我们将
a
11
x
1
+
⋯
+
a
1
n
x
n
=
b
1
⋮
a
m
1
x
1
+
⋯
+
a
m
n
x
n
=
b
m
\begin{array}{c}a_{11} x_{1}+\cdots+a_{1 n} x_{n}=b_{1} \\\vdots \\a_{m 1} x_{1}+\cdots+a_{m n} x_{n}=b_{m}\end{array}
a11x1+⋯+a1nxn=b1⋮am1x1+⋯+amnxn=bm
写成以下形式:
[
a
11
⋮
a
m
1
]
x
1
+
[
a
12
⋮
a
m
2
]
x
2
+
⋯
+
[
a
1
n
⋮
a
m
n
]
x
n
=
[
b
1
⋮
b
m
]
\left[\begin{array}{c}a_{11} \\\vdots \\a_{m 1}\end{array}\right] x_{1}+\left[\begin{array}{c}a_{12} \\\vdots \\a_{m 2}\end{array}\right] x_{2}+\cdots+\left[\begin{array}{c}a_{1 n} \\\vdots \\a_{m n}\end{array}\right] x_{n}=\left[\begin{array}{c}b_{1} \\\vdots \\b_{m}\end{array}\right]
a11⋮am1
x1+
a12⋮am2
x2+⋯+
a1n⋮amn
xn=
b1⋮bm
⟺ [ a 11 ⋯ a 1 n ⋮ ⋮ a m 1 ⋯ a m n ] [ x 1 ⋮ x n ] = [ b 1 ⋮ b m ] \Longleftrightarrow\left[\begin{array}{ccc}a_{11} & \cdots & a_{1 n} \\\vdots & & \vdots \\a_{m 1} & \cdots & a_{m n}\end{array}\right]\left[\begin{array}{c}x_{1} \\\vdots \\x_{n}\end{array}\right]=\left[\begin{array}{c}b_{1} \\\vdots \\b_{m}\end{array}\right] ⟺ a11⋮am1⋯⋯a1n⋮amn x1⋮xn = b1⋮bm
下面,我们将仔细研究这些矩阵(matrices )并定义一些计算规则。我们将在2.3节中回到求解线性方程的问题。
2.2 矩阵
矩阵在线性代数中起着核心作用。它们可以用来紧凑地表示线性方程组,也可以表示线性函数(线性映射),这将在后面2.7节看到。在我们讨论这些话题之前,让我们先定义什么是矩阵,以及我们可以对矩阵做什么样的操作。我们将在第四章看到矩阵的更多性质。
定义2.1(矩阵)
对于任意 m , n ∈ N m, n \in \mathbb{N} m,n∈N, ( m , n ) (m, n) (m,n)实值矩阵(Matrix) A \boldsymbol{A} A是由元素 a i j a_{ij} aij组成的 m ⋅ n m·n m⋅n元组,其中 i = 1 , … , m , j = 1 , … , n i=1, \ldots, m, j=1, \ldots, n i=1,…,m,j=1,…,n,并按照 m m m行和 n n n列的表格形式排序:
A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ a m 1 a m 2 ⋯ a m n ] , a i j ∈ R \boldsymbol{A}=\left[\begin{array}{cccc}a_{11} & a_{12} & \cdots & a_{1 n} \\a_{21} & a_{22} & \cdots & a_{2 n} \\\vdots & \vdots & & \vdots \\a_{m 1} & a_{m 2} & \cdots & a_{m n}\end{array}\right], \quad a_{i j} \in \mathbb{R} A= a11a21⋮am1a12a22⋮am2⋯⋯⋯a1na2n⋮amn ,aij∈R
按惯例, ( 1 , n ) (1,n) (1,n)-矩阵称为行(rows), ( m , 1 ) (m,1) (m,1)-矩阵称为列(columns)。这两个特殊矩阵也称为行或列向量(row/column vectors)。另外,我们称 ( n , n ) (n,n) (n,n)-矩阵为 n n n阶方阵(square matrices),因为它们行数和与列数相等。
如果一个矩阵的所有元素都为0,则称这个矩阵为零矩阵 O \boldsymbol{O} O:
[ 0 0 ⋯ 0 0 0 ⋯ 0 ⋮ ⋮ ⋮ 0 0 ⋯ 0 ] \left[\begin{array}{cccc}0 & 0 & \cdots & 0 \\0 & 0 & \cdots & 0 \\\vdots & \vdots & & \vdots \\0 & 0 & \cdots & 0\end{array}\right] 00⋮000⋮0⋯⋯⋯00⋮0
备注:
R m × n \mathbb{R}^{m \times n} Rm×n是所有 ( m , n ) (m,n) (m,n)实值矩阵的集合。 A ∈ R m × n \boldsymbol{A} \in \mathbb{R}^{m \times n} A∈Rm×n可以等价地表示为 a ∈ R m n \boldsymbol{a} \in \mathbb{R}^{m n} a∈Rmn,方法是将矩阵的所有 n n n列叠加成一个长向量,如图2.4所示。(线性代数(下)的定理 2.17给出解释)

图2.4 通过堆叠其列,矩阵
A
\boldsymbol{A}
A可以表示为长向量
a
\boldsymbol{a}
a。
2.2.1 矩阵加法和乘法
矩阵 A ∈ R m × n , B ∈ R m × n \boldsymbol{A} \in \mathbb{R}^{m \times n}, \boldsymbol{B} \in \mathbb{R}^{m \times n} A∈Rm×n,B∈Rm×n相加定义为其对应元素相加,即:
A + B : = [ a 11 + b 11 ⋯ a 1 n + b 1 n ⋮ ⋮ a m 1 + b m 1 ⋯ a m n + b m n ] ∈ R m × n \boldsymbol{A}+\boldsymbol{B}:=\left[\begin{array}{ccc}a_{11}+b_{11} & \cdots & a_{1 n}+b_{1 n} \\\vdots & & \vdots \\a_{m 1}+b_{m 1} & \cdots & a_{m n}+b_{m n}\end{array}\right] \in \mathbb{R}^{m \times n} A+B:= a11+b11⋮am1+bm1⋯⋯a1n+b1n⋮amn+bmn ∈Rm×n
以下是矩阵加法的一些性质:
对于矩阵
A
∈
R
m
×
n
,
B
∈
R
m
×
n
,
C
∈
R
m
×
n
\boldsymbol{A} \in \mathbb{R}^{m \times n},\boldsymbol{B} \in \mathbb{R}^{m \times n},\boldsymbol{C} \in \mathbb{R}^{m \times n}
A∈Rm×n,B∈Rm×n,C∈Rm×n:
A
+
B
=
B
+
A
\boldsymbol{A}+\boldsymbol{B}=\boldsymbol{B}+\boldsymbol{A}
A+B=B+A
(
A
+
B
)
+
C
=
A
+
(
B
+
C
)
(\boldsymbol{A}+\boldsymbol{B})+\boldsymbol{C}=\boldsymbol{A}+(\boldsymbol{B}+\boldsymbol{C})
(A+B)+C=A+(B+C)
A
+
O
=
A
\boldsymbol{A}+\boldsymbol{O}=\boldsymbol{A}
A+O=A
A
+
(
−
A
)
=
O
\boldsymbol{A}+(-\boldsymbol{A})=\boldsymbol{O}
A+(−A)=O
对于矩阵
A
∈
R
m
×
n
,
B
∈
R
n
×
k
\boldsymbol{A} \in \mathbb{R}^{m \times n}, \boldsymbol{B} \in \mathbb{R}^{n \times k}
A∈Rm×n,B∈Rn×k相乘:
C
=
A
B
∈
R
m
×
k
\boldsymbol{C}=\boldsymbol{A B} \in \mathbb{R}^{m \times k}
C=AB∈Rm×k,
C
\boldsymbol{C}
C的元素
c
i
j
c_{ij}
cij计算如下:
c
i
j
=
∑
l
=
1
n
a
i
l
b
l
j
=
a
i
1
b
1
j
+
a
i
2
b
2
j
+
⋯
+
a
i
n
b
n
j
,
i
=
1
,
…
,
m
,
j
=
1
,
…
,
k
c_{i j}=\sum_{l=1}^{n} a_{i l} b_{l j}=a_{i 1} b_{1 j}+a_{i 2} b_{2 j}+\cdots+a_{i n} b_{nj},\quad i=1, \ldots, m, \quad j=1, \ldots, k
cij=l=1∑nailblj=ai1b1j+ai2b2j+⋯+ainbnj,i=1,…,m,j=1,…,k
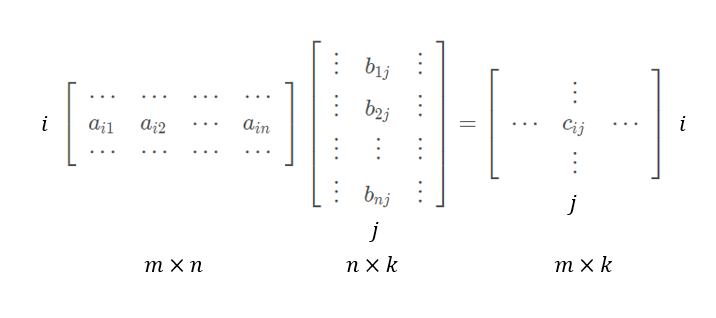
这意味着,为了计算元素 c i j c_{ij} cij,我们将 A \boldsymbol{A} A的第 i i i行的元素与 B \boldsymbol{B} B的第 j j j列元素对应相乘,然后求和。在后面的解析几何中,我们将其称为相应行和列的点积(dot product)。在某些情况下,我们需要明确表示我们在进行乘法运算,我们用符号 A ⋅ B \boldsymbol{A}·\boldsymbol{B} A⋅B来表示矩阵乘法(显式地表示“ ⋅ · ⋅”).
特别地,如果 A \boldsymbol{A} A是一个 n n n阶方阵,则记 A ⋅ A ⋯ A ⏞ k = A k \overbrace{\boldsymbol{A} \cdot \boldsymbol{A} \cdots \boldsymbol{A}}^{k}=\boldsymbol{A}^{k} A⋅A⋯A k=Ak为 A \boldsymbol{A} A的 k k k次幂。
备注:
矩阵只有在“相邻”维度匹配时才能相乘。例如,
n
×
k
n×k
n×k矩阵
A
\boldsymbol{A}
A可以与
k
×
m
k×m
k×m矩阵
B
\boldsymbol{B}
B相乘,且只能从左侧相乘:
A
⏟
n
×
k
B
⏟
k
×
m
=
C
⏟
n
×
m
\underbrace{A}_{n \times k} \underbrace{B}_{k \times m}=\underbrace{C}_{n \times m}
n×k
Ak×m
B=n×m
C
m ≠ n m\not =n m=n,所以 B A \boldsymbol{B}\boldsymbol{A} BA不成立,因为相邻维度不匹配。
备注:
矩阵乘法不是对矩阵元素的逐元素运算,即 c i j ≠ a i j b i j c_{i j} \neq a_{i j} b_{i j} cij=aijbij,即使 A , B \boldsymbol{A},\boldsymbol{B} A,B的尺寸选择得当。实际上,这种逐元素的乘法通常出现在编程语言中,被称为Hadamard积( Hadamard product)。
例 2.3
对于
A
=
[
1
2
3
3
2
1
]
∈
R
2
×
3
,
B
=
[
0
2
1
−
1
0
1
]
∈
R
3
×
2
\boldsymbol{A}=\left[\begin{array}{lll}1 & 2 & 3 \\3 & 2 & 1\end{array}\right] \in \mathbb{R}^{2 \times 3}, \boldsymbol{B}=\left[\begin{array}{cc}0 & 2 \\1 & -1 \\0 & 1\end{array}\right] \in \mathbb{R}^{3 \times 2}
A=[132231]∈R2×3,B=
0102−11
∈R3×2
我们可以得到:
A
B
=
[
1
2
3
3
2
1
]
[
0
2
1
−
1
0
1
]
=
[
2
3
2
5
]
∈
R
2
×
2
\boldsymbol{A B}=\left[\begin{array}{lll}1 & 2 & 3 \\3 & 2 & 1\end{array}\right]\left[\begin{array}{cc}0 & 2 \\1 & -1 \\0 & 1\end{array}\right]=\left[\begin{array}{ll}2 & 3 \\2 & 5\end{array}\right] \in \mathbb{R}^{2 \times 2}
AB=[132231]
0102−11
=[2235]∈R2×2
B A = [ 0 2 1 − 1 0 1 ] [ 1 2 3 3 2 1 ] = [ 6 4 2 − 2 0 2 3 2 1 ] ∈ R 3 × 3 \boldsymbol{B} \boldsymbol{A}=\left[\begin{array}{cc}0 & 2 \\1 & -1 \\0 & 1\end{array}\right]\left[\begin{array}{lll}1 & 2 & 3 \\3 & 2 & 1\end{array}\right]=\left[\begin{array}{ccc}6 & 4 & 2 \\-2 & 0 & 2 \\3 & 2 & 1\end{array}\right] \in \mathbb{R}^{3 \times 3} BA= 0102−11 [132231]= 6−23402221 ∈R3×3
从这个例子中,我们已经可以看出矩阵乘法是不可交换顺序的,即
A
B
≠
B
A
\boldsymbol{A B} \neq \boldsymbol{B A}
AB=BA,另见图2.5的说明。

图2.5 即使矩阵乘法
A
B
\boldsymbol{A B}
AB和
B
A
\boldsymbol{B A}
BA都有定义,结果的维数也可能不同。
定义 2.2(单位矩阵)
在
R
n
×
n
\mathbb{R}^{n \times n}
Rn×n中,单位矩阵( identity matrix):
I
n
:
=
[
1
0
⋯
0
⋯
0
0
1
⋯
0
⋯
0
⋮
⋮
⋱
⋮
⋱
⋮
0
0
⋯
1
⋯
0
⋮
⋮
⋱
⋮
⋱
⋮
0
0
⋯
0
⋯
1
]
∈
R
n
×
n
\boldsymbol{I}_{n}:=\left[\begin{array}{cccccc}1 & 0 & \cdots & 0 & \cdots & 0 \\0 & 1 & \cdots & 0 & \cdots & 0 \\\vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\0 & 0 & \cdots & 1 & \cdots & 0 \\\vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\0 & 0 & \cdots & 0 & \cdots & 1\end{array}\right] \in \mathbb{R}^{n \times n}
In:=
10⋮0⋮001⋮0⋮0⋯⋯⋱⋯⋱⋯00⋮1⋮0⋯⋯⋱⋯⋱⋯00⋮0⋮1
∈Rn×n
为 n × n n×n n×n-矩阵,对角线上为1,其他为0。
现在我们已经定义了矩阵乘法和单位矩阵,让我们看看矩阵的一些性质:
-
结合律(Associativity)
∀ A ∈ R m × n , B ∈ R n × p , C ∈ R p × q : ( A B ) C = A ( B C ) \forall \boldsymbol{A} \in \mathbb{R}^{m \times n}, \boldsymbol{B} \in \mathbb{R}^{n \times p}, \boldsymbol{C} \in \mathbb{R}^{p \times q}:(\boldsymbol{A} \boldsymbol{B}) \boldsymbol{C}=\boldsymbol{A}(\boldsymbol{B C}) ∀A∈Rm×n,B∈Rn×p,C∈Rp×q:(AB)C=A(BC) -
分配律(Distributivity)
∀ A , B ∈ R m × n , C , D ∈ R n × p : ( A + B ) C = A C + B C A ( C + D ) = A C + A D \begin{aligned}\forall \boldsymbol{A}, \boldsymbol{B} \in \mathbb{R}^{m \times n}, \boldsymbol{C}, \boldsymbol{D} \in \mathbb{R}^{n \times p}:(\boldsymbol{A}+\boldsymbol{B}) \boldsymbol{C} &=\boldsymbol{A} \boldsymbol{C}+\boldsymbol{B C} \\\boldsymbol{A}(\boldsymbol{C}+\boldsymbol{D}) &=\boldsymbol{A} \boldsymbol{C}+\boldsymbol{A} \boldsymbol{D}\end{aligned} ∀A,B∈Rm×n,C,D∈Rn×p:(A+B)CA(C+D)=AC+BC=AC+AD
- 与单位矩阵乘法
对于 m ≠ n m \neq n m=n, I m ≠ I n \boldsymbol{I}_{m} \neq \boldsymbol{I}_{n} Im=In.
∀ A ∈ R m × n : I m A = A I n = A \forall \boldsymbol{A} \in \mathbb{R}^{m \times n}: \boldsymbol{I}_{m} \boldsymbol{A}=\boldsymbol{A} \boldsymbol{I}_{n}=\boldsymbol{A} ∀A∈Rm×n:ImA=AIn=A
- 方阵的幂
(
A
k
)
l
=
A
k
l
,
A
k
A
l
=
A
k
+
l
\left(\boldsymbol{A}^{k}\right)^{l}=\boldsymbol{A}^{k l}, \boldsymbol{A}^{k} \boldsymbol{A}^{l}=\boldsymbol{A}^{k+l}
(Ak)l=Akl,AkAl=Ak+l
注意:
(
A
B
)
k
=
(
A
B
)
(
A
B
)
⋯
(
A
B
)
≠
A
k
B
k
(\boldsymbol{A} \boldsymbol{B})^{k}=(\boldsymbol{A} \boldsymbol{B})(\boldsymbol{A} \boldsymbol{B}) \cdots(\boldsymbol{A} \boldsymbol{B}) \neq \boldsymbol{A}^{k} \boldsymbol{B}^{k}
(AB)k=(AB)(AB)⋯(AB)=AkBk
(
A
+
B
)
2
=
A
2
+
A
B
+
B
A
+
B
2
≠
A
2
+
2
A
B
+
B
2
(\boldsymbol{A}+\boldsymbol{B})^{2}=\boldsymbol{A}^{2}+\boldsymbol{A} \boldsymbol{B}+\boldsymbol{B} \boldsymbol{A}+\boldsymbol{B}^{2} \neq \boldsymbol{A}^{2}+2 \boldsymbol{A} \boldsymbol{B}+\boldsymbol{B}^{2}
(A+B)2=A2+AB+BA+B2=A2+2AB+B2
(
A
+
B
)
(
A
−
B
)
=
A
2
−
A
B
+
B
A
−
B
2
≠
A
2
−
B
2
(\boldsymbol{A}+\boldsymbol{B})(\boldsymbol{A}-\boldsymbol{B})=\boldsymbol{A}^{2}-\boldsymbol{A} \boldsymbol{B}+\boldsymbol{B} \boldsymbol{A}-\boldsymbol{B}^{2} \neq \boldsymbol{A}^{2}-\boldsymbol{B}^{2}
(A+B)(A−B)=A2−AB+BA−B2=A2−B2
2.2.2 逆和转置
定义 2.3(逆)
考虑一个方阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n,使得矩阵 B ∈ R n × n \boldsymbol{B} \in \mathbb{R}^{n \times n} B∈Rn×n: A B = I n = B A \boldsymbol{A}\boldsymbol{B}=\boldsymbol{I_{n}}=\boldsymbol{B}\boldsymbol{A} AB=In=BA,则 B \boldsymbol{B} B称为 A \boldsymbol{A} A的逆(Inverse),表示为: A − 1 \boldsymbol{A}^{-1} A−1
不过,不是所有矩阵 A \boldsymbol{A} A都有逆 A − 1 \boldsymbol{A}^{-1} A−1。如果矩阵的逆存在,则称它为正则/可逆/非奇异(regular/invertible/nonsingular),否则称为奇异/不可逆(singular/noninvertible)。当矩阵逆存在时,这个逆是唯一的。在第2.3节中,我们将讨论通过求解线性方程组来计算矩阵逆的一般方法。
备注(2×2矩阵逆的存在性):
考虑一个矩阵:
A
:
=
[
a
11
a
12
a
21
a
22
]
∈
R
2
×
2
\boldsymbol{A}:=\left[\begin{array}{ll}a_{11} & a_{12} \\a_{21} & a_{22}\end{array}\right] \in \mathbb{R}^{2 \times 2}
A:=[a11a21a12a22]∈R2×2
将它与
A
′
\boldsymbol{A}'
A′相乘
A
′
:
=
[
a
22
−
a
12
−
a
21
a
11
]
\boldsymbol{A}^{\prime}:=\left[\begin{array}{cc}a_{22} & -a_{12} \\-a_{21} & a_{11}\end{array}\right]
A′:=[a22−a21−a12a11]
我们得到:
A A ′ = [ a 11 a 22 − a 12 a 21 0 0 a 11 a 22 − a 12 a 21 ] = ( a 11 a 22 − a 12 a 21 ) I \boldsymbol{A} \boldsymbol{A}^{\prime}=\left[\begin{array}{cc}a_{11} a_{22}-a_{12} a_{21} & 0 \\0 & a_{11} a_{22}-a_{12} a_{21}\end{array}\right]=\left(a_{11} a_{22}-a_{12} a_{21}\right) \boldsymbol{I} AA′=[a11a22−a12a2100a11a22−a12a21]=(a11a22−a12a21)I
因此:当且仅当
a
11
a
22
−
a
12
a
21
≠
0
a_{11} a_{22}-a_{12} a_{21} \neq 0
a11a22−a12a21=0
A
−
1
=
1
a
11
a
22
−
a
12
a
21
[
a
22
−
a
12
−
a
21
a
11
]
\boldsymbol{A}^{-1}=\frac{1}{a_{11} a_{22}-a_{12} a_{21}}\left[\begin{array}{cc}a_{22} & -a_{12} \\-a_{21} & a_{11}\end{array}\right]
A−1=a11a22−a12a211[a22−a21−a12a11]
在后面的4.1节中,我们将会知道 a 11 a 22 − a 12 a 21 a_{11} a_{22}-a_{12} a_{21} a11a22−a12a21是2x2矩阵的行列式(determinant)。此外,我们一般可以用行列式来检验矩阵是否可逆。
例 2.4:逆矩阵
对于矩阵
A
=
[
1
2
1
4
4
5
6
7
7
]
,
B
=
[
−
7
−
7
6
2
1
−
1
4
5
−
4
]
\boldsymbol{A}=\left[\begin{array}{lll}1 & 2 & 1 \\4 & 4 & 5 \\6 & 7 & 7\end{array}\right], \quad \boldsymbol{B}=\left[\begin{array}{ccc}-7 & -7 & 6 \\2 & 1 & -1 \\4 & 5 & -4\end{array}\right]
A=
146247157
,B=
−724−7156−1−4
由于
A
B
=
I
=
B
A
\boldsymbol{A}\boldsymbol{B}=\boldsymbol{I}=\boldsymbol{B}\boldsymbol{A}
AB=I=BA,因此两个矩阵互逆。
以下是逆的一些重要性质:
A
A
−
1
=
I
=
A
−
1
A
\boldsymbol{A} \boldsymbol{A}^{-1}=\boldsymbol{I}=\boldsymbol{A}^{-1} \boldsymbol{A}
AA−1=I=A−1A
( A B ) − 1 = B − 1 A − 1 (\boldsymbol{A B})^{-1}=\boldsymbol{B}^{-1} \boldsymbol{A}^{-1} (AB)−1=B−1A−1
(
A
+
B
)
−
1
≠
A
−
1
+
B
−
1
(\boldsymbol{A}+\boldsymbol{B})^{-1} \neq \boldsymbol{A}^{-1}+\boldsymbol{B}^{-1}
(A+B)−1=A−1+B−1
类似于
1
2
+
4
=
1
6
≠
1
2
+
1
4
\frac{1}{2+4}=\frac{1}{6} \neq \frac{1}{2}+\frac{1}{4}
2+41=61=21+41
定义 2.4(转置)
对于矩阵
A
∈
R
m
×
n
\boldsymbol{A} \in \mathbb{R}^{m \times n}
A∈Rm×n,若矩阵
B
∈
R
n
×
m
\boldsymbol{B} \in \mathbb{R}^{n \times m}
B∈Rn×m满足
b
i
j
=
a
j
i
b_{i j}=a_{j i}
bij=aji,则
B
\boldsymbol{B}
B称为
A
\boldsymbol{A}
A的转置(Transpose),记作
B
=
A
⊤
\boldsymbol{B}=\boldsymbol{A}^{\top}
B=A⊤
A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ a m 1 a m 2 ⋯ a m n ] , 则 A T = [ a 11 a 21 ⋯ a m 1 a 12 a 22 ⋯ a m 2 ⋮ ⋮ ⋮ a 1 n a 2 n ⋯ a n m ] \boldsymbol{A}=\left[\begin{array}{cccc}a_{11} & a_{12} & \cdots & a_{1 n} \\a_{21} & a_{22} & \cdots & a_{2 n} \\\vdots & \vdots & & \vdots \\a_{m 1} & a_{m 2} & \cdots & a_{m n}\end{array}\right], \text { 则 } \boldsymbol{A}^{\mathrm{T}}=\left[\begin{array}{cccc}a_{11} & a_{21} & \cdots & a_{m 1} \\a_{12} & a_{22} & \cdots & a_{m 2} \\\vdots & \vdots & & \vdots \\a_{1 n} & a_{2 n} & \cdots & a_{n m}\end{array}\right] A= a11a21⋮am1a12a22⋮am2⋯⋯⋯a1na2n⋮amn , 则 AT= a11a12⋮a1na21a22⋮a2n⋯⋯⋯am1am2⋮anm
通常, A ⊤ \boldsymbol{A}^{\top} A⊤可以通过将 A \boldsymbol{A} A的列写为 A ⊤ \boldsymbol{A}^{\top} A⊤的行来获得。
( A ⊤ ) ⊤ = A \left(\boldsymbol{A}^{\top}\right)^{\top}=\boldsymbol{A} (A⊤)⊤=A
( A + B ) ⊤ = A ⊤ + B ⊤ (\boldsymbol{A}+\boldsymbol{B})^{\top}=\boldsymbol{A}^{\top}+\boldsymbol{B}^{\top} (A+B)⊤=A⊤+B⊤
( A B ) ⊤ = B ⊤ A ⊤ (\boldsymbol{A B})^{\top}=\boldsymbol{B}^{\top} \boldsymbol{A}^{\top} (AB)⊤=B⊤A⊤
矩阵
A
\boldsymbol{A}
A的主对角线(main diagonal
)(有时称为“principal diagonal”、“primary diagonal”、“leading diagonal”或“major diagonal”)是元素
A
i
j
,
i
=
j
A_{ij},i=j
Aij,i=j的集合。
定义 2.5(对称矩阵)
若对于矩阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n有 A = A ⊤ \boldsymbol{A}=\boldsymbol{A}^{\top} A=A⊤,则称它是对称的(symmetric)。
注意,只有 ( n , n ) (n,n) (n,n)-矩阵可以是对称的。另外,如果矩阵 A \boldsymbol{A} A可逆,则 A ⊤ \boldsymbol{A}^{\top} A⊤也是可逆的,且 ( A − 1 ) ⊤ = ( A ⊤ ) − 1 = : A − ⊤ \left(\boldsymbol{A}^{-1}\right)^{\top}=\left(\boldsymbol{A}^{\top}\right)^{-1}=: \boldsymbol{A}^{-\top} (A−1)⊤=(A⊤)−1=:A−⊤
备注:(对称矩阵的和与积)
对称矩阵
A
,
B
∈
R
n
×
n
\boldsymbol{A}, \boldsymbol{B} \in \mathbb{R}^{n \times n}
A,B∈Rn×n之和总是对称的。然而,尽管他们积总是有定义的,但通常不是对称的:
[
1
0
0
0
]
[
1
1
1
1
]
=
[
1
1
0
0
]
\left[\begin{array}{ll}1 & 0 \\0 & 0\end{array}\right]\left[\begin{array}{ll}1 & 1 \\1 & 1\end{array}\right]=\left[\begin{array}{ll}1 & 1 \\0 & 0\end{array}\right]
[1000][1111]=[1010]
2.2.3 与标量相乘
让我们看看当矩阵与标量 λ ∈ R \lambda \in \mathbb{R} λ∈R相乘时会发生什么。若有 A ∈ R m × n \boldsymbol{A} \in \mathbb{R}^{m \times n} A∈Rm×n, λ ∈ R \lambda \in \mathbb{R} λ∈R,则 λ A = K , K i j = λ a i j \lambda \boldsymbol{A}=\boldsymbol{K}, K_{i j}=\lambda a_{i j} λA=K,Kij=λaij。实际上, λ \lambda λ对矩阵的每个元素进行了缩放。对于 λ , ψ ∈ R \lambda, \psi \in \mathbb{R} λ,ψ∈R,以下公式成立:
-
结合律:
( λ ψ ) C = λ ( ψ C ) , C ∈ R m × n (\lambda \psi) \boldsymbol{C}=\lambda(\psi \boldsymbol{C}), \quad \boldsymbol{C} \in \mathbb{R}^{m \times n} (λψ)C=λ(ψC),C∈Rm×n -
λ ( B C ) = ( λ B ) C = B ( λ C ) = ( B C ) λ , B ∈ R m × n , C ∈ R n × k \lambda(\boldsymbol{B C})=(\lambda \boldsymbol{B}) \boldsymbol{C}=\boldsymbol{B}(\lambda \boldsymbol{C})=(\boldsymbol{B C}) \lambda, \quad \boldsymbol{B} \in \mathbb{R}^{m \times n}, \boldsymbol{C} \in \mathbb{R}^{n \times k} λ(BC)=(λB)C=B(λC)=(BC)λ,B∈Rm×n,C∈Rn×k
这允许我们任意移动标量的位置。
-
( λ C ) ⊤ = C ⊤ λ ⊤ = C ⊤ λ = λ C ⊤ since λ = λ ⊤ for all λ ∈ R (\lambda \boldsymbol{C})^{\top}=\boldsymbol{C}^{\top} \lambda^{\top}=\boldsymbol{C}^{\top} \lambda=\lambda \boldsymbol{C}^{\top} \text { since } \lambda=\lambda^{\top} \text { for all } \lambda \in \mathbb{R} (λC)⊤=C⊤λ⊤=C⊤λ=λC⊤ since λ=λ⊤ for all λ∈R
-
分配律:
( λ + ψ ) C = λ C + ψ C , C ∈ R m × n (\lambda+\psi) \boldsymbol{C}=\lambda \boldsymbol{C}+\psi \boldsymbol{C}, \quad \boldsymbol{C} \in \mathbb{R}^{m \times n} (λ+ψ)C=λC+ψC,C∈Rm×n
λ ( B + C ) = λ B + λ C , B , C ∈ R m × n \lambda(\boldsymbol{B}+\boldsymbol{C})=\lambda \boldsymbol{B}+\lambda \boldsymbol{C}, \quad \boldsymbol{B}, \boldsymbol{C} \in \mathbb{R}^{m \times n} λ(B+C)=λB+λC,B,C∈Rm×n
例 2.5(分配律)
如果我们定义:
C
:
=
[
1
2
3
4
]
C:=\left[\begin{array}{ll}1 & 2 \\3 & 4\end{array}\right]
C:=[1324]
那么对任意
λ
,
ψ
∈
R
\lambda, \psi \in \mathbb{R}
λ,ψ∈R,我们可以得到:
(
λ
+
ψ
)
C
=
[
(
λ
+
ψ
)
1
(
λ
+
ψ
)
2
(
λ
+
ψ
)
3
(
λ
+
ψ
)
4
]
=
[
λ
+
ψ
2
λ
+
2
ψ
3
λ
+
3
ψ
4
λ
+
4
ψ
]
=
[
λ
2
λ
3
λ
4
λ
]
+
[
ψ
2
ψ
3
ψ
4
ψ
]
=
λ
C
+
ψ
C
\begin{aligned}(\lambda+\psi) \boldsymbol{C} &=\left[\begin{array}{cc}(\lambda+\psi) 1 & (\lambda+\psi) 2 \\(\lambda+\psi) 3 & (\lambda+\psi) 4\end{array}\right]=\left[\begin{array}{cc}\lambda+\psi & 2 \lambda+2 \psi \\3 \lambda+3 \psi & 4 \lambda+4 \psi\end{array}\right] \\&=\left[\begin{array}{cc}\lambda & 2 \lambda \\3 \lambda & 4 \lambda\end{array}\right]+\left[\begin{array}{cc}\psi & 2 \psi \\3 \psi & 4 \psi\end{array}\right]=\lambda \boldsymbol{C}+\psi \boldsymbol{C}\end{aligned}
(λ+ψ)C=[(λ+ψ)1(λ+ψ)3(λ+ψ)2(λ+ψ)4]=[λ+ψ3λ+3ψ2λ+2ψ4λ+4ψ]=[λ3λ2λ4λ]+[ψ3ψ2ψ4ψ]=λC+ψC
2.2.4 分块矩阵
矩阵除了可以看作一个整体,还可以看作是由若干个子矩阵拼接而成,将矩阵用若干水平线和竖直线分成几块子块,称为矩阵的分块。
矩阵 A \boldsymbol{A} A按行分块:
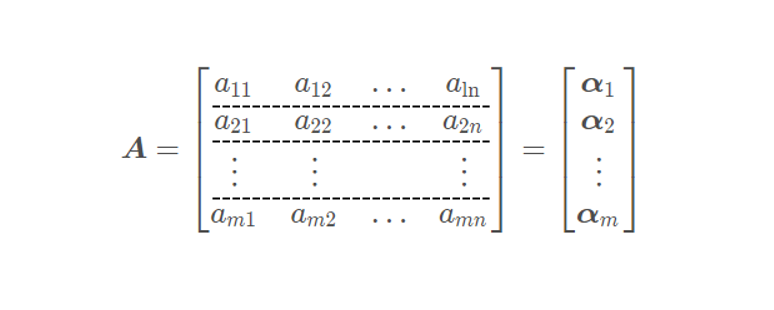
其中
α
i
=
[
a
i
1
,
a
i
2
,
⋯
,
a
i
n
]
,
i
=
1
,
2
,
⋯
,
m
\boldsymbol{\alpha} _{i}=[a_{i1},a_{i2},\cdots,a_{in}],i=1,2,\cdots,m
αi=[ai1,ai2,⋯,ain],i=1,2,⋯,m
矩阵
A
\boldsymbol{A}
A按列分块:
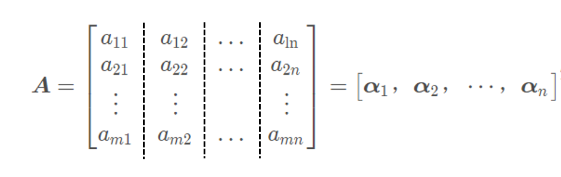
其中
α
j
=
[
a
1
j
,
a
2
j
,
⋯
,
a
m
j
]
T
,
j
=
1
,
2
,
⋯
,
n
\boldsymbol{\alpha} _{j}=[a_{1j},a_{2j},\cdots,a_{mj}]^T,j=1,2,\cdots,n
αj=[a1j,a2j,⋯,amj]T,j=1,2,⋯,n
矩阵 A \boldsymbol{A} A混合分块:

分块矩阵的运算:
在保证子块运算满足矩阵运算条件的前提下,有以下运算:
[ A 1 A 2 A 3 A 4 ] + [ B 1 B 2 B 3 B 4 ] = [ A 1 + B 1 A 2 + B 2 A 3 + B 3 A 4 + B 4 ] \begin{bmatrix} \boldsymbol{A}_{1}&\boldsymbol{A}_{2}\\ \boldsymbol{A}_{3}&\boldsymbol{A}_{4}\end{bmatrix}+\begin{bmatrix} \boldsymbol{B}_{1}&\boldsymbol{B}_{2}\\ \boldsymbol{B}_{3}&\boldsymbol{B}_{4} \end{bmatrix}=\begin{bmatrix} \boldsymbol{A}_{1}+\boldsymbol{B}_{1}&\boldsymbol{A}_{2}+\boldsymbol{B}_{2}\\ \boldsymbol{A}_{3}+\boldsymbol{B}_{3}&\boldsymbol{A}_{4}+\boldsymbol{B}_{4} \end{bmatrix} [A1A3A2A4]+[B1B3B2B4]=[A1+B1A3+B3A2+B2A4+B4]
[ A 1 A 2 A 3 A 4 ] [ B 1 B 2 B 3 B 4 ] = [ A 1 B 1 + A 2 B 3 A 1 B 2 + A 2 B 4 A 3 B 1 + A 4 B 3 A 3 B 2 + A 4 B 4 ] \begin{bmatrix} \boldsymbol{A}_{1}&\boldsymbol{A}_{2}\\ \boldsymbol{A}_{3}&\boldsymbol{A}_{4}\end{bmatrix}\begin{bmatrix} \boldsymbol{B}_{1}&\boldsymbol{B}_{2}\\ \boldsymbol{B}_{3}&\boldsymbol{B}_{4} \end{bmatrix}=\begin{bmatrix} \boldsymbol{A}_{1}\boldsymbol{B}_{1}+\boldsymbol{A}_2\boldsymbol{B}_3&\boldsymbol{A}_{1}\boldsymbol{B}_{2}+\boldsymbol{A}_{2}\boldsymbol{B}_{4}\\ \boldsymbol{A}_{3}\boldsymbol{B}_1+\boldsymbol{A}_4\boldsymbol{B}_{3}&\boldsymbol{A}_{3}\boldsymbol{B}_2+\boldsymbol{A}_4\boldsymbol{B}_{4} \end{bmatrix} [A1A3A2A4][B1B3B2B4]=[A1B1+A2B3A3B1+A4B3A1B2+A2B4A3B2+A4B4]
[ A 1 A 2 A 3 A 4 ] ⊤ = [ A 1 ⊤ A 3 ⊤ A 2 ⊤ A 4 ⊤ ] \begin{bmatrix} \boldsymbol{A}_{1}&\boldsymbol{A}_{2}\\ \boldsymbol{A}_{3}&\boldsymbol{A}_{4}\end{bmatrix}^\top=\begin{bmatrix} \boldsymbol{A}_{1}^\top&\boldsymbol{A}_{3}^\top\\ \boldsymbol{A}_{2}^\top&\boldsymbol{A}_{4}^\top\end{bmatrix} [A1A3A2A4]⊤=[A1⊤A2⊤A3⊤A4⊤]
[ A 1 O O A 4 ] n = [ A 1 n O O A 4 n ] \begin{bmatrix} \boldsymbol{A}_{1}&\boldsymbol{O}\\ \boldsymbol{O}&\boldsymbol{A}_{4}\end{bmatrix}^n=\begin{bmatrix} \boldsymbol{A}_{1}^n&\boldsymbol{O}\\ \boldsymbol{O}&\boldsymbol{A}_{4}^n\end{bmatrix} [A1OOA4]n=[A1nOOA4n]
[ A 1 O O A 4 ] − 1 = [ A 1 − 1 O O A 4 − 1 ] \begin{bmatrix} \boldsymbol{A}_{1}&\boldsymbol{O}\\ \boldsymbol{O}&\boldsymbol{A}_{4}\end{bmatrix}^{-1}=\begin{bmatrix} \boldsymbol{A}_{1}^{-1}&\boldsymbol{O}\\ \boldsymbol{O}&\boldsymbol{A}_{4}^{-1}\end{bmatrix} [A1OOA4]−1=[A1−1OOA4−1]
[ O A 2 A 3 O ] − 1 = [ O A 3 − 1 A 2 − 1 O ] \begin{bmatrix} \boldsymbol{O}&\boldsymbol{A}_{2}\\ \boldsymbol{A}_{3}&\boldsymbol{O}\end{bmatrix}^{-1}=\begin{bmatrix} \boldsymbol{O}&\boldsymbol{A}_{3}^{-1}\\ \boldsymbol{A}_{2}^{-1}&\boldsymbol{O}\end{bmatrix} [OA3A2O]−1=[OA2−1A3−1O]
例子:
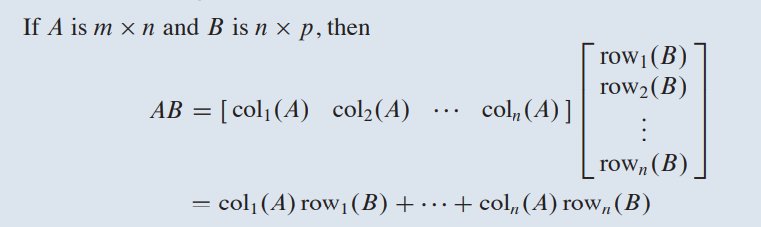
2.2.5 线性方程组的紧凑表示
如果我们考虑考虑线性方程组
2 x 1 + 3 x 2 + 5 x 3 = 1 4 x 1 − 2 x 2 − 7 x 3 = 8 9 x 1 + 5 x 2 − 3 x 3 = 2 \begin{array}{l}2 x_{1}+3 x_{2}+5 x_{3}=1 \\4 x_{1}-2 x_{2}-7 x_{3}=8 \\9 x_{1}+5 x_{2}-3 x_{3}=2\end{array} 2x1+3x2+5x3=14x1−2x2−7x3=89x1+5x2−3x3=2
利用矩阵的乘法法则,我们可以把这个方程组写成更紧凑的形式
[
2
3
5
4
−
2
−
7
9
5
−
3
]
[
x
1
x
2
x
3
]
=
[
1
8
2
]
\left[\begin{array}{ccc}2 & 3 & 5 \\4 & -2 & -7 \\9 & 5 & -3\end{array}\right]\left[\begin{array}{l}x_{1} \\x_{2} \\x_{3}\end{array}\right]=\left[\begin{array}{l}1 \\8 \\2\end{array}\right]
2493−255−7−3
x1x2x3
=
182
可以注意到, x 1 x_1 x1缩放第一列, x 2 x_2 x2缩放第二列, x 3 x_3 x3缩放第三列。
一般来说,线性方程组可以用矩阵形式表示为 A x = b \boldsymbol{A}\boldsymbol{x}=\boldsymbol{b} Ax=b;且乘积 A x \boldsymbol{A}\boldsymbol{x} Ax是 A \boldsymbol{A} A每一列的(线性)组合。我们将在2.5节中更详细地讨论线性组合。
2.3 线性方程组的求解
翻译自:
《MATHEMATICS FOR MACHINE LEARNING》作者是 Marc Peter Deisenroth,A Aldo Faisal 和 Cheng Soon Ong























 6784
6784











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










