【机器学习】生成对抗网络（GAN）

本文为机器学习的学习总结，讲解生成对抗网络（GAN）。欢迎在评论区与我交流 😃

导论

GAN 的基本概念

在 GAN 中，我们需要训练一个生成器（Generator），输入一个向量，让机器生成一些影像或诗词：

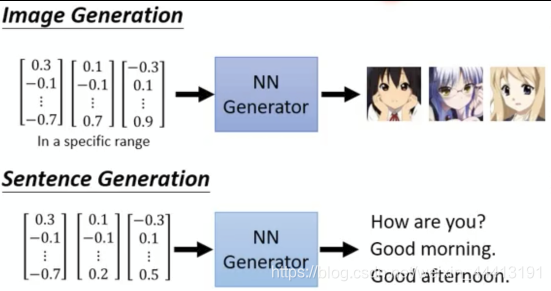
条件生成器输入已知的东西，而不是随机的向量，例如输入文字，让机器输出对的图片。条件生成器有很多应用，之后会详细讲解。

生成器是一个神经网络，即一个函数。在影像生成中，输出的图片就是高维向量。例如输入向量，输出头像，向量每一维代表一个特征：

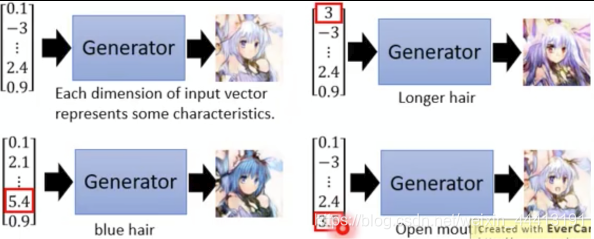
与此同时，我们还会训练识别器（discriminator），识别器也是一个神经网络。例如输入图片，输出代表真实度的数值。

例如下面的例子，枯叶蝶是生成器，麻雀是识别器。枯叶蝶为了避免被捕食会不断进化，而麻雀为了捕食猎物也会不断进化：

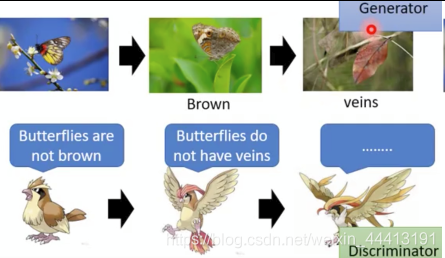
识别器判断图片生成器生成的还是真实的图片，此时标准可能是是否为彩色等简单的标准。下一代的生成器想办法骗过第一代的识别器，从而进化到第二代；然后识别器也进化到第二代，学会判断第二代生成器与真实图片的差异。如此往复，不断进化。像天敌和被捕食者的关系。

当然对抗关系只是一种比喻，从另一个角度看也可以是互助的关系。例如学生画画（生成器），老师告诉学生如何画（识别器）。老师的标准不断严格，学生的水平也不断提高。

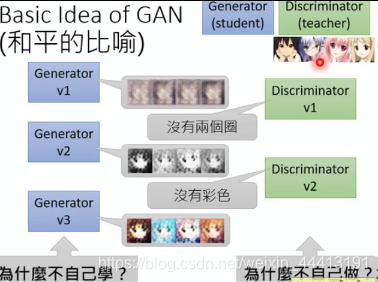
那么生成器为什么不自己学？识别器为什么不自己做？这两个问题我们后面会讲到。

这里用语言描述算法步骤：

首先随机初始化生成器和识别器。

在每次迭代中：

1. 固定生成器 $G$，更新识别器参数。数据库给出范例，训练目标是：数据库范例输入时，输出 1；生成器图像输入时，输出 0.
2. 固定识别器 $D$，调整生成器参数。生成器需要骗过识别器，希望生成器输出的图像，识别器能给高分，从而使生成的图像更真实。

实际中将生成器和识别器的神经网络和起来形成一个更大的神经网络，其中中间某层（隐藏层）输出一个图像。调参时固定一部分层的参数，调另一部分。

然后我们对算法进行数学描述：

初始化 $D$ 的参数 ${\theta }_d$ 和 $G$ 的参数 ${\theta }_g$。

在每次迭代中：

更新识别器参数 ${\theta }_d$

1. 在数据库中选取 $m$ 个样本 { x 1 , … , x m } \{x^1,…,x^m\} { x1,…,xm}

2. 从随机分布中选取 $m$ 个样本 { z 1 , … , z m } \{z^1,…,z^m\} { z1,…,zm}

3. 计算生成器结果（产生图片） { x ~ 1 , … , x ~ m } \{\tilde{x}^1,…,\tilde{x}^m\} { x~