在ADS中进行稳定性分析（以避免K稳定性因子的局限性）-理论部分

在ADS中进行稳定性分析（以避免K稳定性因子的局限性）-理论部分

在进行MMIC设计时，我使用经典的K因子进行稳定性判断。但是总是非常疑惑，好像高增益和稳定性不能兼得一样。即使晶体管栅长也不大，加上稳定电路增益都不到10dB了（让K因子大于1），不加能有15dB的样子，真的是难受。因此专门来学习研究一下功放稳定性的理论，并记录。

这部分理论对我还是非常难懂的，主要是自动控制部分的理论，当初没有学习过。
参考：https://www.youtube.com/watch?v=kVPzU7Eszk4&t=300s
推荐学习视频：13_奈奎斯特稳定性判据
ADS工程的官方下载链接：How to Design a Stable High Frequency Amplifier

需要我的ADS工程可以在评论区留言，只是在原来基础上小改了一下，不过大家估计不感兴趣。

1、K稳定性因子的局限性

K稳定性因子文章：Instabilities diagnosis and the role of K in microwave circuits

K因子可以依据S参数进行计算，满足以下条件即为绝对稳定：
$$K=\frac{1-|S_{11}{|}^2-|S_{11}{|}^2+|\Delta {|}^2}{2|S_{12}{S}_{21}|}>1$$

其中：
$$\Delta =|S_{11}{S}_{22}-S_{12}{S}_{21}|<1$$

在功率放大器的设计中，很多人都只使用K稳定性因子来判断稳定性，比如之前的设计案例：
宽带Doherty放大器ADS仿真（带版图）、ADS使用记录之AB类功放设计、ADS使用记录之超宽带功放设计、ADS使用记录之功率放大器设计等等。

但是，K稳定性因子具备局限性。只有原本的电路在开路、短路情况都稳定的时候，K因子的计算才能用于判断稳定性，原文见Stability and Power-Gain Invariants of Linear Twoports：

因此，K因子用在实际的稳定性测试时更加准确，用在设计阶段是缺乏说服力的。

在实际测试时，我们可以先测量开路、短路是否稳定，然后使用S参数计算稳定性因子来判断电路在一个频段内是否绝对稳定。

在电路设计仿真时，使用K因子判断，需要默认电路在开路、短路情况下稳定，这样不严谨。

2、反馈系统的稳定性判定简易案例

在进行运算放大器、功率放大器电路的设计时，都需要进行稳定性分析，这样的系统往往都是反馈系统。可能有人以为自己没有额外在电路系统中引入反馈，但是在射频系统中反馈是无处不在的，例如微带线之间的耦合、非线性器件内部的响应等等。理想的放大器也并非单纯的电流源，存在许多内部环路：

2.1、不稳定的简单案例

对于下面的一个简单放大器的反馈系统，我们可以计算其闭环增益（Closed-loop gain, Acl）如下图所示：

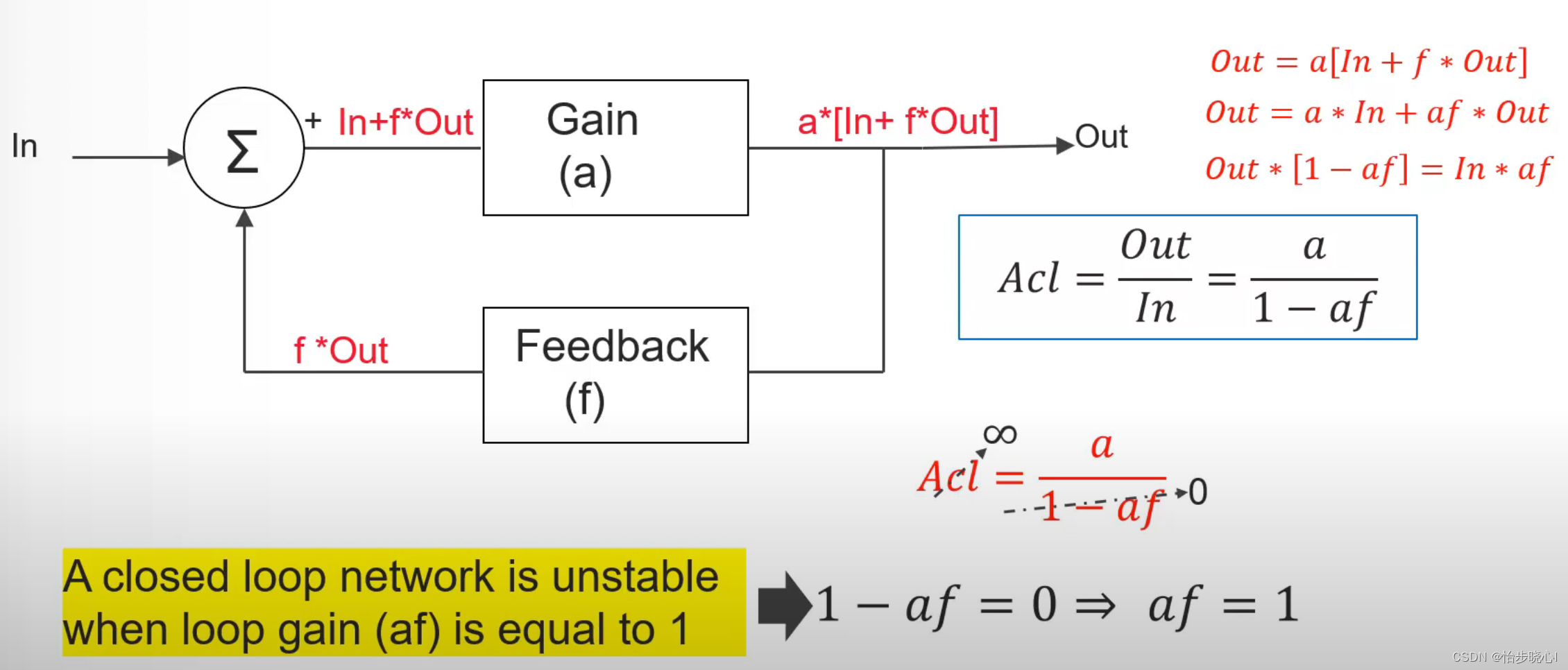
显然，闭环增益Acl是用下式计算的：
$$Acl=\frac{Out}{In}=\frac{a}{1-af}$$
当1-af=0时，系统的闭环增益为无穷大，由此造成了不稳定现象。

更加直观一点，举个例子：

1. 假设一开始输入是幅度为1的正弦波，反馈回来的信号是同相的原信号1/10幅度；
2. 那么第二次环路实际的输入是1.1，反馈回来的信号是同相的原信号1/10幅度也就是0.11；
3. 那么第三次环路实际的输入是1.21，这样依次循环，输出就会越来越大，造成不稳定。

为充分说明系统不稳定反馈的影响，运行ADS工程中的02_Transient_AC，得到的实际的效果就是：

2.2、从Laplace域判断稳定性的简单例子

闭环增益ACL一般都是使用Laplace域来进行表征的，如：
$$Acl(s)=\frac{A(s)}{1-A(s)F(s)}$$
简单回顾一下Laplace变换公式，如下：
$$F(s)={\int }_0^{\infty }f(t)e^{-st}dt$$
当然，还有一个延迟性质的变换需要回顾：
$$e^{at}\iff \frac{1}{s-a}$$
那么闭环增益ACL可以写成下面的形式：
$$Acl(s)=\frac{A(s)}{1-A(s)F(s)}=\frac{(s-z1)(s-z2)...}{(s-p1)(s-p2)...}$$
假设一个简单的形式，我们使用延迟性质的变换分离极点并转换到时域：
$$\frac{K}{(s-p1)(s-p2)}=\frac{A_1}{(s-p_1)}+\frac{A_2}{(s-p_2)}\iff A_1{e}^{p_{1}t}+A_2{e}^{p_{2}t}$$
那么，如果拥有右半平面的极点，p就会大于0，那么最终的结果就会指数发散，如下图右侧：

3、柯西幅角定理

3.1、反馈系统的框图和开环传递函数

反馈系统的框图和开环传递函数如下，参考[1]（美）KATSUHIKO OGATA著；卢伯英，佟明安译. 现代控制工程 第5版[M]. 北京：电子工业出版社, 2017.05.：

对于上图的一般框图，类似可得闭环增益Acl（闭环传递函数）如下，其中分母的正负和2.1小节的不同，这是因为两个框图的相加点的符号不同罢了，实际是一致的：
$$Acl=\varphi (s)=\frac{G(s)}{1+G(s)H(s)}$$

3.2、柯西幅角原理

这部分参考：奈奎斯特稳定性判据的详细推导
这位博主写的非常详细了，对小白非常友好，我这边搬点过来，hihi

3.2.1 F(s)的相角变化

先问一个问题：当s从闭合曲线 Γ 上任意一点顺时针沿 Γ 运动一周后，F(s)的相角变化了多少？
我们以一个简单的传递函数为例：
$$\mathrm{F}(\mathrm{s})=\mathrm{s}-(2+2j)$$

其中传递函数的零点为 z = 2 + 2j，F(s)的相角变化就是 ∠(s - z) 积累的角度，以下根据闭环曲线 Γ 与零点Z的关系分成两种情况讨论：
①若选取的闭环曲线 Γ 未包含 z = 2 + 2j ，那么随着点s在闭环曲线上运动一周，我们以z为原点建立坐标系，发现 ∠s - z 最后没有积累角度，F(s)的相角变化为0 。可以发现，这个角度实际上是先变大后变小的，最后回到0，相当于转了半天白干了：

②若选取的闭环曲线 Γ 包含 z = 2 + 2j ，那么随着点s在闭环曲线上运动一周，s回到了原来位置上，但此时 ∠s - z 顺时针积累了2π的角度，F(s)的 相角变化为2π。虽然最后也回到了起点，但是实际上是转了一圈：

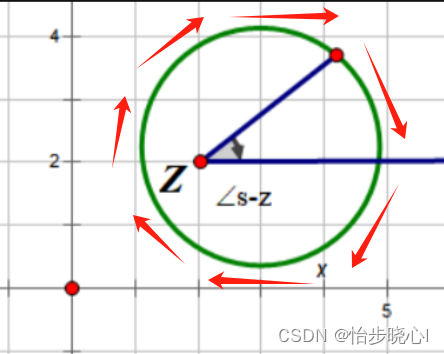
所以我们得到结论：

• 对于闭合曲线 Γ 外的零点和极点，对应的相角变化为0
• 对于闭合曲线 Γ 内的零点和极点，对应的相角变化为2π

注：闭合曲线 Γ 不通过F(s)的任一零、极点。F(s)的零、极点要么在曲线里面，要么在曲线外面

3.2.2 拓展至多个零点、极点

传递函数同时有零点、极点，如何分析F(s)的相角变化？假设：
$$\mathrm{F}(\mathrm{s})=\frac{\left(\mathrm{s}-{\mathrm{z}}_1\right)\left(\mathrm{s}-{\mathrm{z}}_2\right)}{\left(\mathrm{s}-{\mathrm{p}}_1\right)\left(\mathrm{s}-{\mathrm{p}}_2\right)}$$
F(s)可以化为：
$$\frac{{\mathrm{A}}_{{\mathrm{z}}_1}{\mathrm{A}}_{{\mathrm{z}}_2}}{{\mathrm{A}}_{{\mathrm{p}}_1}{\mathrm{A}}_{{\mathrm{p}}_2}}{\mathrm{e}}^{({\phi }^{{\mathrm{z}}_1}+{\phi }^{{\mathrm{z}}_2}-({\phi }^{{\mathrm{p}}_1}+{\phi }^{{\mathrm{p}}_2}))}$$
于是我们可以得到F(s)的相角变化：
$$\delta \angle F(\mathrm{s})=\delta \angle (\mathrm{s}-{\mathrm{z}}_1)+\delta \angle (\mathrm{s}-{\mathrm{z}}_2)-\delta \angle (\mathrm{s}-{\mathrm{p}}_1)-\delta \angle (\mathrm{s}-{\mathrm{p}}_2)$$
极点p1、p2作为分母，与零点z1、z2产生的相角变化相反

3.2.3 柯西幅角原理本体

F(s)绕平面原点的圈数只和F(s)被闭合曲线 Γ 包围F(s)的零点和极点的代数和有关
设F(s)有Z个零点和P个极点被 Γ 包围，则s沿曲线 Γ 顺时针运动一周时，F(s)变化的相角为 2π(P - Z)，在F(s)平面上，闭合曲线 ΓF 逆时针包围原点的圈数为（也就是极点数减去零点数）：
$$\mathrm{R}=\mathrm{P}-\mathrm{Z}$$

• R： ΓF 逆时针包围原点的圈数
• P：F(s)在s平面闭合曲线 Γ 内被包围的极点数
• Z：F(s)在s平面闭合曲线 Γ 内被包围的零点数

R > 0 和 R < 0分别表示 曲线ΓF 逆时针包围原点和顺时针包围原点的圈数，R = 0 表示曲线 ΓF 不包围原点

为什么是 ΓF 包围原点的圈数，而不是其它点呢？这段我也没搞懂，就直接背着了，原话是：
因为我们计算得到F(s)相角的变化为2π的整数倍，在F(s)平面中，要使F(s)对应的点变化的相角为2π的整数倍，那么闭合曲线 ΓF 里一定要包含原点，所以我们取包含原点的圈数

3.2.4 柯西幅角原理的简单示例

下面的例子，画个圈圈住了四个零点和两个极点，那么最终的F（s）的结果·就是$\mathrm{R}=\mathrm{P}-\mathrm{Z}=-2$，需要顺时针绕原点两圈，如右图所示：

4、基于环路增益的系统稳定性判断

如何将幅角原理与系统稳定性结合起来呢？在此进行分析
这部分参考：奈奎斯特稳定性判据的详细推导

4.1、选择合适的复变函数F(s)来表征系统

4.1.1、如何选择F(s)才能与系统稳定性结合

☆ F(s)选择成：
$$1+\mathrm{G}(\mathrm{s})\mathrm{H}(\mathrm{s})$$
为什么？1+G(s)H(s)有什么特殊意义吗？
对于这样一个负反馈系统：

其中：
$$\mathrm{G}\left(\mathrm{s}\right)=\frac{\mathrm{s}+2}{\mathrm{s}+5},\mathrm{H}\left(\mathrm{s}\right)=\frac{1}{\mathrm{s}+4}$$
那么：

发现1+G(s)H(s)的分子分母具有特殊的意义：

▷1+G(s)H(s)的零点为闭环传递函数的极点

▷1+G(s)H(s)的极点为开环传递函数的极点

那么使用1+G(s)H(s)就可以同时包含开环传函和闭环传函的极点

4.1.2、 1+G(s)H(s) 的优点

在控制系统中是利用开环传递函数来判断闭环系统的稳定性的

若我们将s平面的闭合曲线 Γ 取成整个右半平面（我理解是因为右半平面的极点会导致不稳定性）

那么对于F(s)=1+G(s)H(s)来说，我们令F(s)在右半平面的零点数和极点数为 Z 和 P

如果右半平面中闭环传递函数的极点数为0，则系统稳定，即Z = 0 系统稳定

4.1.1中分析了，F(s)的极点为开环传递函数的极点，开环传输函数是已知的，即 P是已知的

在F(s)平面中，闭合曲线 ΓF 逆时针包围原点的圈数为：
$$\mathrm{R}=\mathrm{P}-\mathrm{Z}$$

至此，P、Z的意义转化为：

▷R： ΓF 逆时针包围原点的圈数
▷P：开环传递函数在右半平面内的极点数，P是已知的
▷Z：闭环传递函数在右半平面内的极点数，若Z = 0系统稳定

简单来说，我们已知F(s)的极点个数（，F(s)的极点为开环传递函数的极点，开环传输函数是已知的，即 P是已知的）。随后使用柯西幅角定理可以求得包围原点的圈数R，这样就能计算得到闭环传递函数在右半平面内的极点数 Z，进而进行稳定性判断。

4.2、闭合曲线 Γ 的选择

我们只关注右半坐标轴的极点，因为这会带来不稳定。那么如何设计闭合曲线 Γ ，使得能取满整个右半平面？

幅角原理中要求闭合曲线 Γ 不通过 F(s)的任一零、极点，则 Γ 的选择与虚轴上有无零极点有关。
1. G(s)H(s) 无虚轴上的极点
我们以一个以原点为圆心，半径无穷大的半圆表示右半平面：

2. G(s)H(s) 有虚轴上的极点
若虚轴上有极点，为了避免闭合曲线 Γ 通过零、极点，我们可以想办法绕过去，则画一个半径无穷小的半圆绕过极点：

4.3、R的求取和实际的曲线绘制

R等于 ΓGH 逆时针包围F(s)平面 点(-1 , j0) 的圈数，那么我们将 ΓGH 画出来就可以计算R的大小了

这样选择无穷然后画⚪是比较书面的说法。假设我们已知了开环传输函数GH和s=jw这个简单的变换，我们可以让w从0到无穷，然后绘制出传输函数的实部虚部图：

clc
close all
clear

C=tf([1 1],[1 0.1]);
Sys=tf([1],[1 0.4 1]);
H=tf([1],[1 5]);
GH=C*Sys*H
% matlab自带的绘制函数
nyquist(GH)
% 自己对角度w进行扫描
w=0.001:0.001:10;
s=j*w;
my_GH=(s + 1)./(s.^4 + 5.5*s.^3 + 3.54*s.^2 + 5.3*s + 0.5);
figure
plot(real(my_GH),imag(my_GH))
hold on
w=-0.001:-0.001:-10;
s=j*w;
my_GH=(s + 1)./(s.^4 + 5.5*s.^3 + 3.54*s.^2 + 5.3*s + 0.5);
plot(real(my_GH),imag(my_GH))

可以看到上面的图没有对 点(-1 , j0) 绕圈，因此系统R=0，而给出的函数GH没有右半平面的极点，因此P=0，从而系统稳定。

4.4、不稳定的例子

对上面的函数直接乘以5：

得到结果是顺时针绕了两圈，因此R=-2：

因此：
$$\mathrm{Z}=\mathrm{P}-\mathrm{R}=0+2=2$$

由于闭环传递函数在右半平面内的极点数，若Z = 0系统稳定，因此上面的系统是不稳定的。

4.5、在ADS中使用奈奎斯特稳定性判据-简单案例

4.5.1、不稳定案例

对于下面的系统，由于此处使用的是合路（上面第四部分的分析是输入和反馈相减），因此R等于 ΓGH 逆时针包围F(s)平面 点(1 , j0) 的圈数：

运行仿真，发现顺时针绕1有1圈的样子，因此R=-1：

对于上面的系统，仿真发现在开环时是稳定的，因此可以认为其没有在右半平面内的极点数P=0：

因此：
$$\mathrm{Z}=\mathrm{P}-\mathrm{R}=0+1=1$$

由于闭环传递函数在右半平面内的极点数，若Z = 0系统稳定，因此上面的系统是不稳定的。在ADS中将环路连接上去：

仿真发现是不稳定的，判断有效：

4.5.2、稳定案例

修改FeedBack电路：

重新在开路情况下仿真，发现结果不绕（1，0）有圈数：


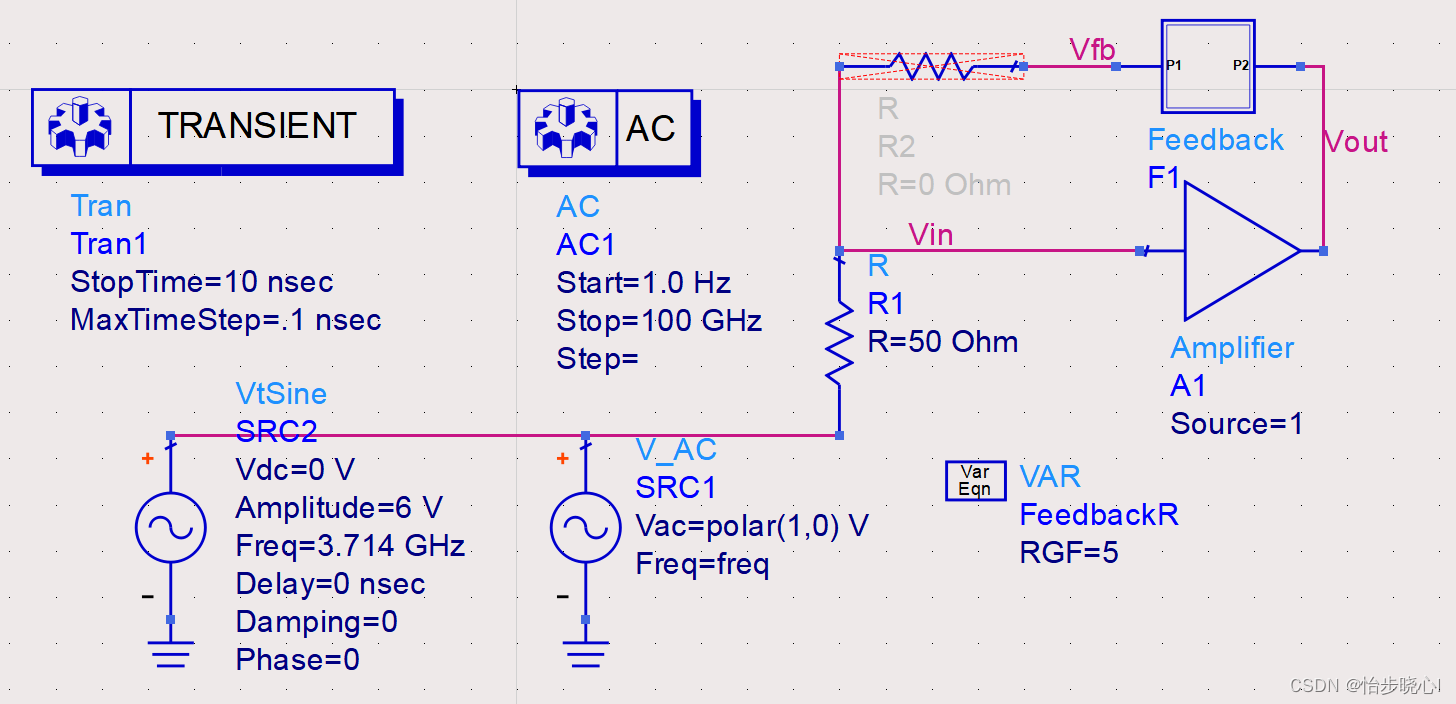
因此系统稳定：
$$\mathrm{Z}=\mathrm{P}-\mathrm{R}=0+0=0$$
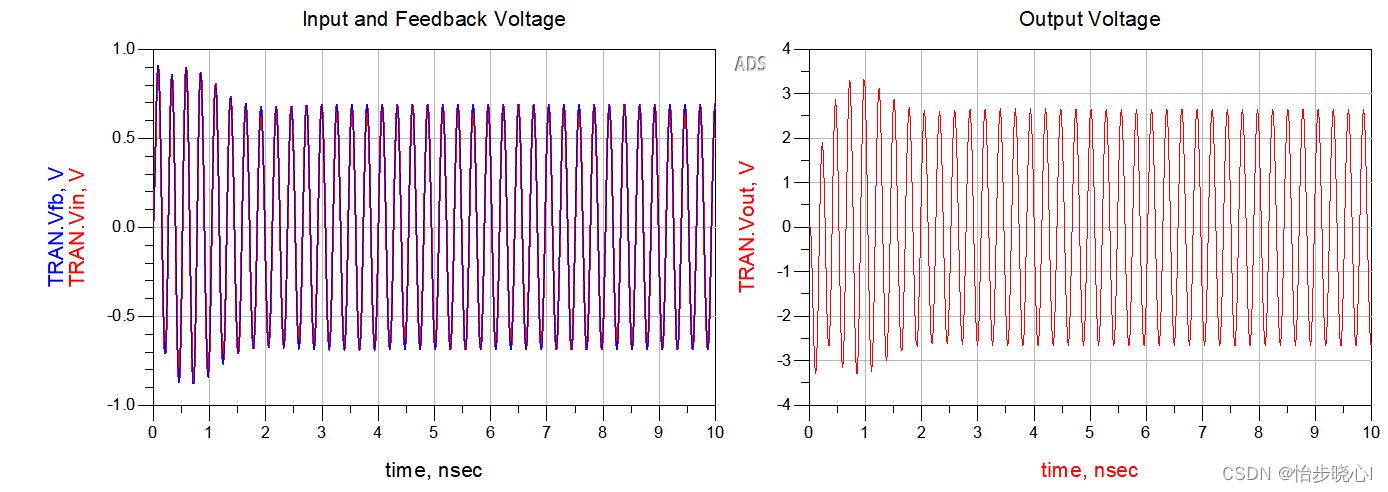
为了对判断进行验证，加上反馈：

发现是非常稳定的：