【学习笔记】直观理解拉格朗日问题

直观理解拉格朗日问题

学习视频：BV1HP4y1Y79e

up主：王木头学科学

什么是拉格朗日乘数法

拉格朗日乘数法是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法。这种方法将一个有 n 个变量与 k 个约束条件的最优化问题转换为一个有 n + k 个变量的方程组的极值问题，其变量不受任何约束。

这种方法引入了一种新的标量未知数，即拉格朗日乘数：约束方程的梯度（gradient）的线性组合里每个向量的系数。

---

设给定二元函数 $z=ƒ(x,y)$ 和附加条件 $\phi (x,y)=0$，为寻找 $z=ƒ(x,y)$ 在附加条件下的极值点，先构造拉格朗日函数

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QCMFGiWv-1639449802020)(https://bkimg.cdn.bcebos.com/formula/3ff19b95cd9f967ec90851e6a5dc9f64.svg)]

，其中 $\lambda$ 为参数。

令 $F(x,y,\lambda )$ 对 $x$ ，$y$ 和 $\lambda$ 的一阶偏导数等于零，即
$$\{\begin{array}{l}{F}_x^{\prime }=f_x^{\prime }(x,y)+\lambda {\phi }_x^{\prime }(x,y)\\ F_y^{\prime }=f_y^{\prime }(x,y)+\lambda {\phi }_y^{\prime }(x,y)\\ F_{\lambda }^{\prime }={\phi }_x(x,y)=0\end{array}$$
由上述方程组解出 $x$，$y$ 及 $\lambda$ ，如此求得的$(x,y)$，就是函数 $z=ƒ(x,y)$ 在附加条件 $\phi (x,y)=0$ 下的可能极值点。

若这样的点只有一个，由实际问题可直接确定此即所求的点。

---

左图显示的是约束条件与目标函数的等高线的相交情况，其中黄色箭头代表约束条件在该点的梯度方向，而蓝色箭头代表的是目标函数在该点的梯度方向。

我们可以看出，只有在约束条件曲线与目标函数等高线相切点（图中红色点），二者的梯度方向相同，只有方向一致，我们才有可能让其相加为0。这个时候我们调整参数 $\lambda$ ，使两个梯度大小相等、方向相反，这样便找到了极值点。

在该情况下，只有 $\alpha$ 和 $\beta$ 两个约束条件起作用了，这两个梯度的向量相加的方向应该与目标函数的梯度的方向相反。而其他的约束条件没有起作用，那么他们的系数 $\lambda$ 均应为0。

由此，我们可以得出以下结论：

凹凸集的定义

在一个集合中任取两点，若这两点之间的线段属于集合内，那么称之为凸集，反之则称为非凸集。

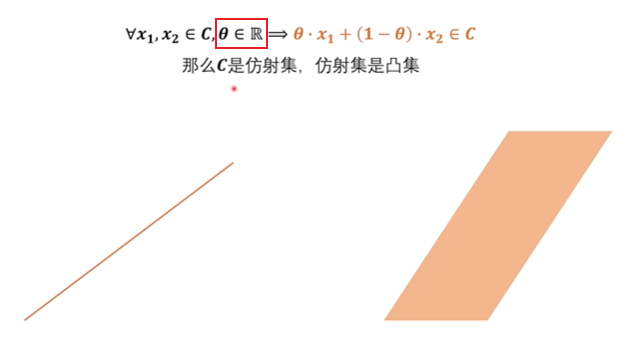
仿射集对 $\theta$ 没有限制在0~1之间，其一定是凸集。

直线将空间分成了一半，这一般也是凸集。

凹凸函数的定义

由图我们可知，凸函数有最小值，凹函数有最大值。（这里凸和凹与直观感受不同是因为国内外翻译问题）

而凹凸函数在定义上即满足凸函数，又满足凹函数。

在凸函数上求最小值和在凹函数上求最大值，都可以看作是凸问题。我们更习惯于求最小值，故遇到凹函数我们在其前面加一个负号，将其转化成凸函数。

但如果我们遇到非凸问题该怎么办？那么我们就看他的对偶问题，对偶问题永远是凸问题。

原问题转化为对偶问题

在这里为什么要求变量为 $\lambda$ 和 $\nu$ 的函数的最大值？

之所以是最大值（Max），是因为线性组合相加为L，这样可以使此条件下的$f_0(x)$最小。

针对x在可行域和不在可行域内的结果相比较，若在可行域内值小于不在可行域内，则忽略较大值，即二者中取最小值。这样便将$x$的可行域范围情况隐含在了拉格朗日函数中。

在转化成对偶问题时，我们相当于调换一下计算顺序，先将 $\lambda$ 和 $\nu$ 看作常数，把 $x$ 看作变量求最小值，即对偶函数。在对偶函数的基础上添加求 $\lambda$ 和 $\nu$ 的最大值和 $\lambda \ge 0$ 的约束条件，即为对偶问题。

先求内部绿色框，即将 $x$ 看作变量求函数最小值，再求红色框，即把 $\lambda$ 和 $\nu$ 看作变量求最大值。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6HwJaMjW-1639449802029)(C:\Users\42280\AppData\Roaming\Typora\typora-user-images\image-20211212164154493.png)]

这两部分相互等价，即可将其看作以 $x$ 为变量求梯度，梯度等于零即得最小值，故可将其以约束条件的形式表示。

为什么对偶问题恒为凸问题

对于这种情况，我们可知，不管原函数时什么函数，绿框内的均为常数，蓝框内的为变量，且均为一阶线性的关系，那么该对偶函数即既凸又凹的函数。

由于我们的对偶问题是要对这个对偶函数 $g(\lambda ,\nu )$ 求最大值，那么对偶函数是个凹函数。

凸优化问题即该问题目标函数为凸函数，可行域为凸集。而对偶问题我们在对偶函数前加个负号就是凸问题了，约束条件 $\lambda \ge 0$ 也表明可行域为凸集，故对偶问题一定是凸优化问题。

（这块儿我感觉怪怪的…）

原问题和对偶问题的等价性讨论

我们将原问题转化成对偶问题来解决，但是原问题和对偶问题不一定是完全等价的，证明如下：

可知，原问题的解恒大于等于对偶问题的解。

在原问题中，$x$ 的可行域为D，其中D为约束条件；在对偶问题中，$x$ 的可行域为全空间（${\mathbb{R}}^n$），即通过放缩来找到 $\min L$ 的最小值。

由于原问题限制 $u\le 0$ ，所以 G1 为原问题的可行域，那么最小值为 P*；对于对偶问题，可将 $t+{\lambda }^T\cdot u$ 看作一条直线，则直线斜率为 $-\lambda$ 。在上图红色框中，我们先确定斜率，找到该直线与 t 轴产生的截距最小值。

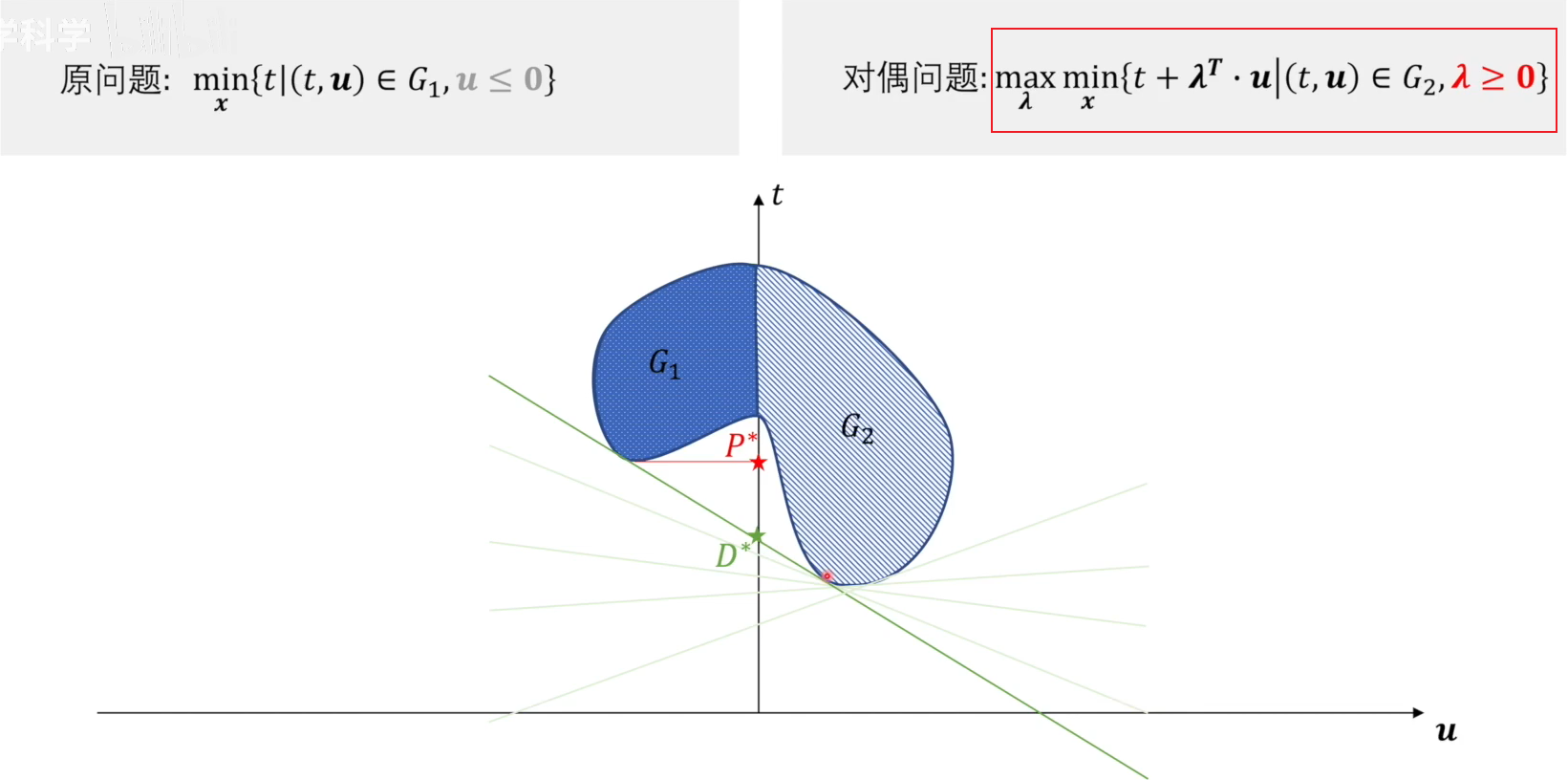
在确定与可行域 G2 的交点后，再来找满足条件的 $\lambda$ 的最大值，即改变直线的斜率，使其与可行域 G1 和 G2 同时相切。只有在这种情况下的斜率找到的最优切线才能使得最大最小同时满足。此实的截距 D* 即是我们要找的对偶问题的解。

若 P* $\ge$ D*，则为若对偶关系；若 P* = D*，则为强对偶关系。

在可行域为凸集的情况下，可以得到强对偶关系。

由于可行域的最小值在 $u\le 0$ 这部分，而 $-\lambda \le 0$ 使得直线斜率最大只能取到0。

综上，只有凸集存在强对偶关系。

Slater条件

那么我们是不是可以说，只要是一个凸优化问题，他就是强对偶关系呢？

在数学上，严谨来说，一个凸优化问题如果是强对偶关系，那么它必须满足Slater条件。

其中 $relintD$ 表示 $x$ 属于可行域内部点，不能在边界上。

直观理解如下图：

即在凸集内部存在一个点。（我也不太懂😥）

KKT条件

一个强对偶关系问题它的必要条件是KKT条件。

只要该问题为强对偶关系，那么一定满足KKT条件；而满足KKT条件的不一定为强对偶关系。

最大熵和神经网络中对偶问题的体现

最大熵：

同时使用对偶问题，我们将参数 P 确定，而 $\lambda$ 就可以看作一个超参数，通过机器学习的方法进行调参。

神经网络：

我们遇到的大部分问题可能不是凸优化问题，而神经网络的隐藏层可以将问题拆分，把不是凸优化的因素给屏蔽掉，在输出层局部形成一个凸优化的场景，在该场景下用凸优化的方案来解决问题。但是这里也只是解决了局部问题，所以局部问题带来的改变和成果还有反向传播至隐藏层中，对整个神经网络进行调整，不断循环该过程，直至到达最优的效果。